In a book, the answer for a particular question is expressed as here m represents mass, a represent acceleration, l represent length. The unit of b should be :-
meter
/sec
The correct Answer is:C
To find the unit of b given the expression
b=mak√1+2klma
we will analyze the dimensions of each component step by step.
Step 1: Identify the dimensions of each variable
- Mass (m) has the dimension (M).
- Acceleration (a) has the dimension (LT−2).
- Length (l) has the dimension (L).
- k is an unknown constant, and we will determine its dimensions later.
Step 2: Analyze the term mak
We need to find the dimensions of mak.
1. The dimension of ma is:
(m)⋅(a)=(M)⋅(LT−2)=(MLT−2)
2. Now, let's denote the dimension of k as (K). Therefore, the dimension of mak is:
(MLT−2)(K)=(MLT−2)(K)
Step 3: Analyze the term 2klma
Next, we need to analyze 2klma.
1. The dimension of kl is:
(K)⋅(L)=(KL)
2. The dimension of ma is already calculated as (MLT−2).
3. Therefore, the dimension of 2klma is:
(KL)(MLT−2)=(K)(MT−2)
Step 4: Set the dimension of 1+2klma
For the expression 1+2klma to be dimensionless, the dimensions of 2klma must also be dimensionless. This implies:
(K)=(MT−2)
Step 5: Substitute back to find the dimension of mak
Now we can substitute back to find the dimension of mak:
mak=(MLT−2)(MT−2)=(L)
Step 6: Analyze the square root term
The term √1+2klma is dimensionless, so it does not contribute any dimensions.
Step 7: Combine the results
Thus, the dimension of b is:
b=mak√1+2klma=(L)⋅(1)=(L)
Conclusion
The unit of b is the unit of length, which is typically expressed in meters (m).
Final Answer
The unit of b should be: meters (m).
- Mass (m) has the dimension (M).
- Acceleration (a) has the dimension (LT−2).
- Length (l) has the dimension (L).
- k is an unknown constant, and we will determine its dimensions later.
We need to find the dimensions of mak.
(m)⋅(a)=(M)⋅(LT−2)=(MLT−2)
(MLT−2)(K)=(MLT−2)(K)
Next, we need to analyze 2klma.
(K)⋅(L)=(KL)
(KL)(MLT−2)=(K)(MT−2)
For the expression 1+2klma to be dimensionless, the dimensions of 2klma must also be dimensionless. This implies:
(K)=(MT−2)
Now we can substitute back to find the dimension of mak:
mak=(MLT−2)(MT−2)=(L)
The term √1+2klma is dimensionless, so it does not contribute any dimensions.
Thus, the dimension of b is:
b=mak√1+2klma=(L)⋅(1)=(L)
The unit of b is the unit of length, which is typically expressed in meters (m).
The unit of b should be: meters (m).
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (O-1) Multiple Correct Type Questions.3videos
UNIT & DIMENSIONS, BASIC MATHS AND VECTOR
- BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (O-1) ComprehensionType Questions.3videos
UNIT & DIMENSIONS, BASIC MATHS AND VECTOR
- BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (S-2)7videos
UNIT & DIMENSIONS, BASIC MATHS AND VECTOR
- BOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - MATHS18videos
TEST PAPERS
- BOOK - ALLENCHAPTER - WAVE OPTICSEXERCISE - Exercise 2 (Previous Year Questions)7videos
WAVE OPTICS
Similar Questions
Knowledge Check
- Question 1 - Select One
An unknown quantity ''α'' is expressed as α=2maβlog(1+2βlma) where m = mass, a = acceleration l = length, The unit of α should be
AmeterBm/sCm/s2Ds−1 - Question 2 - Select One
Dimensions of an unknown quantity ,ϕ=maαlog(1+αlma) where m= mass, a= acceleration and l=length are
A[MLT−2]B[MT−2]C[M0LT0]D[ML−3] - Question 3 - Select One
Assertion: In the relationf=12l√Tm, where symbols have standard meaning , m represent linear mass density.
Reason: The frequency has the dimensions linear of time.AIf both assertion and reason are true and reason is the correct explation of assertion.BIf both assertion but reason is not the correct explanation of assertion.CIf assertion is true but reason is false.DIf both assertion and reason are false.
Study the diagram given below and answer the questions based on it.
△ represents Persons who like Reading
 represents Persons who like Cycling
represents Persons who like Cycling
□ represents Persons who like Trekking
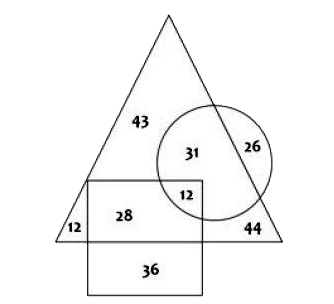
How many persons like Trekking and Reading but not Cycling ?
A. 12
B. 31
C. 44
D. 28View SolutionIf pressure can be expressed as P=ba√1+kθt3ma
where k is the Boltzmann's constant, θ is the temperature, t is the time and a and b are constants, then dimensional formula of b is equal to the dimensional formula ofView SolutionIf the equation ∣∣∣√(x−1)2+y2−√(x+1)2+y2∣∣∣=k represents a hyperbola , then k belongs to the set
View SolutionStudy the diagram given below and answer the questions based on it.
△ represents Persons who like Reading
∘ represents Persons who like Cycling
□ represents Persons who like Trekking
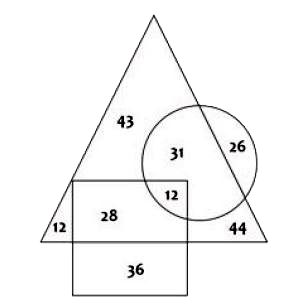
How many persons line Reading and Cycling but not Trekking
A. 31
B. 12
C. 26
D. 28View SolutionIn two different system of unit an acceleration is represented by the same number, whilst a velocity is represented by numbers in the ratio 1:3. The ratio of unit of length and time are
View Solution

