A body moves in anticlockwise direction on a circular path in the x-y plane. The radius of the circular path is 5m and its centre is at the origin. In a certain interval of time, displacement of the body is obesrved to be 6m in the positive y-direction. Which of the following is true ?
Its initial position vector is 5ˆi m
Its initial position vector is (−3ˆi+4ˆj) m.
Its final position vector is (4ˆi+3ˆj)m.
Its final position vector is 6ˆj m.
The correct Answer is:C
To solve the problem, we need to analyze the motion of a body moving anticlockwise on a circular path centered at the origin (0,0) with a radius of 5 meters. The displacement of the body is given as 6 meters in the positive y-direction. We will determine the initial and final position vectors of the body based on the given information.
1. Understanding the Circular Path:
- The body is moving anticlockwise on a circular path with a radius of 5 meters. This means the maximum distance from the center (origin) to any point on the path is 5 meters.
2. Identifying the Displacement:
- The displacement of the body is 6 meters in the positive y-direction. This indicates that the body has moved vertically upwards from its initial position.
3. Setting Up the Coordinate System:
- Let's define our coordinate system:
- The x-axis is horizontal, and the y-axis is vertical.
- The center of the circular path is at the origin (0,0).
4. Using Pythagorean Theorem:
- Since the radius of the circular path is 5 meters, we can use the Pythagorean theorem to find the position of the body.
- Let the initial position of the body be at point (x, y). The displacement of 6 meters in the positive y-direction means that if the body started at (x, y), its new position after the displacement will be (x, y + 6).
5. Finding the Initial Position:
- The initial position must satisfy the equation of the circle:
x2+y2=52=25
- After the displacement, the new position (x, y + 6) must also satisfy the circle's equation:
x2+(y+6)2=25
6. Setting Up the Equations:
- From the first equation:
x2+y2=25(1)
- Expanding the second equation:
x2+(y2+12y+36)=25(2)
- From (2), we can substitute x2 from (1):
25+12y+36=25
- Simplifying gives:
12y+36=0⟹y=−3
7. Finding x:
- Substitute y=−3 back into equation (1):
x2+(−3)2=25⟹x2+9=25⟹x2=16⟹x=4 or −4
- Since the body is moving anticlockwise, we can choose x=4 (in the first quadrant).
8. Initial Position Vector:
- The initial position vector is:
Initial Position=4^i−3^j meters
9. Final Position Vector:
- After the displacement of 6 meters in the positive y-direction:
Final Position=4^i+(−3+6)^j=4^i+3^j meters
10. Conclusion:
- The final position vector of the body is 4^i+3^j meters.
Answer:
The correct option is: Its final position vector is 4^i+3^j meters.
- The body is moving anticlockwise on a circular path with a radius of 5 meters. This means the maximum distance from the center (origin) to any point on the path is 5 meters.
- The displacement of the body is 6 meters in the positive y-direction. This indicates that the body has moved vertically upwards from its initial position.
- Let's define our coordinate system:
- The x-axis is horizontal, and the y-axis is vertical.
- The center of the circular path is at the origin (0,0).
- Since the radius of the circular path is 5 meters, we can use the Pythagorean theorem to find the position of the body.
- Let the initial position of the body be at point (x, y). The displacement of 6 meters in the positive y-direction means that if the body started at (x, y), its new position after the displacement will be (x, y + 6).
- The initial position must satisfy the equation of the circle:
x2+y2=52=25
- After the displacement, the new position (x, y + 6) must also satisfy the circle's equation:
x2+(y+6)2=25
- From the first equation:
x2+y2=25(1)
- Expanding the second equation:
x2+(y2+12y+36)=25(2)
- From (2), we can substitute x2 from (1):
25+12y+36=25
- Simplifying gives:
12y+36=0⟹y=−3
- Substitute y=−3 back into equation (1):
x2+(−3)2=25⟹x2+9=25⟹x2=16⟹x=4 or −4
- Since the body is moving anticlockwise, we can choose x=4 (in the first quadrant).
- The initial position vector is:
Initial Position=4^i−3^j meters
- After the displacement of 6 meters in the positive y-direction:
Final Position=4^i+(−3+6)^j=4^i+3^j meters
- The final position vector of the body is 4^i+3^j meters.
The correct option is: Its final position vector is 4^i+3^j meters.
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (O-2) Multiple Correct Type Questions.7videos
UNIT & DIMENSIONS, BASIC MATHS AND VECTOR
- BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (O-2) Comprehension Type Questions.9videos
UNIT & DIMENSIONS, BASIC MATHS AND VECTOR
- BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (O-1) Matrix match type Questions.4videos
UNIT & DIMENSIONS, BASIC MATHS AND VECTOR
- BOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - MATHS18videos
TEST PAPERS
- BOOK - ALLENCHAPTER - WAVE OPTICSEXERCISE - Exercise 2 (Previous Year Questions)7videos
WAVE OPTICS
Similar Questions
A boy travelled in a circular path and reached to the initial position 'O'. If the radius of the circle is 7 m. Find the distance covered and the displacement of the body.
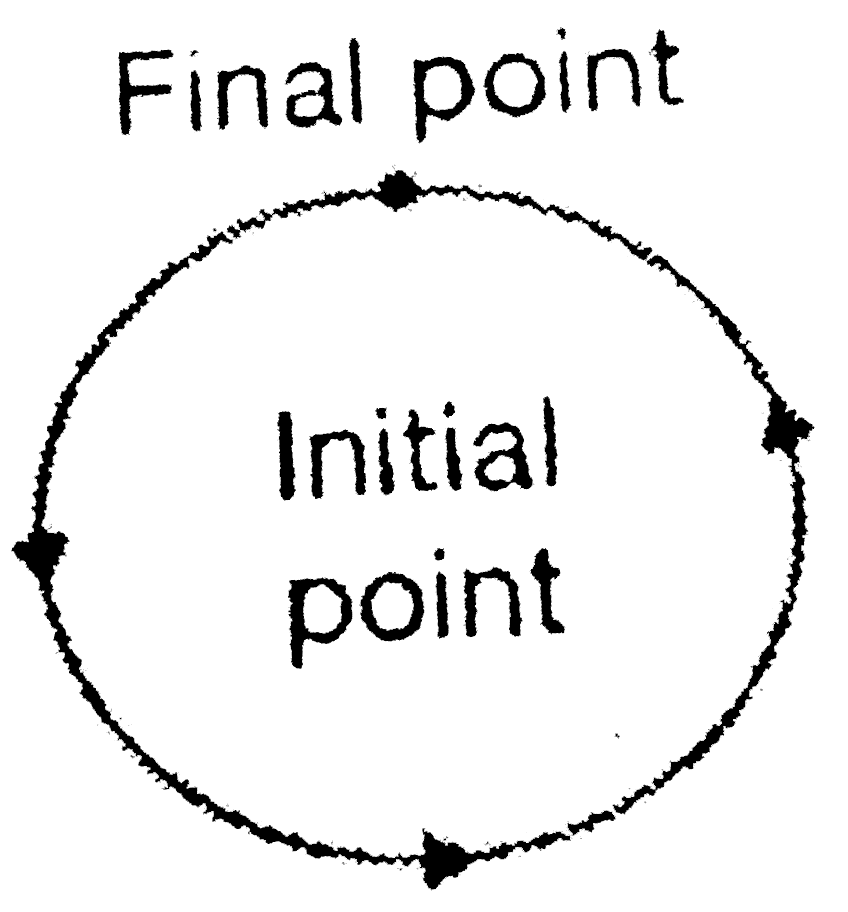 View Solution
View SolutionA boy travelled in a circular path and reached to the initial position 'O'. If the radius of the circle is 7 m. Find the distance covered and the displacement of the body.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
In insect moves on a circular path of radius 7m. Find the maximum magnitude of displacement of the insect
A7mB14πmC7πmD14m - Question 2 - Select One
A body of mass m moves in a circular path with uniform angular velocity. The motion of the body has constant
AAccelerationBVelocityCMomentumDKinetic energy - Question 3 - Select One
A body move in a circular path of radius 20 cm. If it completes two and a half revolution along the circular path, the distance and displacement of the body are
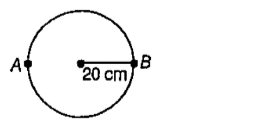 A40 cm,0B314 cm,0C314 cm, 40 cmD628 cm, 314 cm
A40 cm,0B314 cm,0C314 cm, 40 cmD628 cm, 314 cm
If a body completes I round of a circular path of radius 7 cm, its displacement is
View SolutionA body is moving along a circular path of radius R. What will be the distance travelled and displacement of the body when it completes half a revolution ?
View SolutionA body is moving along a circular path with constant speed. If the direction of rotation is reversed and the speed is doubled,
View SolutionA body moves with a speed of 2πms−1 in a cirular path of radius 1 m , then the time taken to compete one revolution is ________.
View SolutionA body of mass 2 kg is rotating on a circular path of radius 0.5 m, with an angular velocity of 20 rad/s. If the radius of the path is doubled, then the new angular velocity will be
View Solution

