A physical quantity is a phyical property of a phenomenon , body, or substance , that can be quantified by measurement.
The magnitude of the components of a vector are to be considered dimensionally distinct. For example , rather than an undifferentiated length unit L, we may represent length in the x direction as Lx, and so forth. This requirement status ultimately from the requirement that each component of a physically meaningful equation (scaler or vector) must be dimensionally consistent . As as example , suppose we wish to calculate the drift S of a swimmer crossing a river flowing with velocity Vx and of widht D and he is swimming in direction perpendicular to the river flow with velocity Vy relation to river, assuming no use of directed lengths, the quantities of interest are then Vx,Vy both dimensioned as LT , S the drift and D width of river both having dimension L. with these four quantities, we may conclude tha the equation for the drift S may be written : S∝VaxVbyDc
Or dimensionally L=(LT)a+b×(L)c from which we may deduce that a+b+c=1 and a+b=0, which leaves one of these exponents undetermined. If, however, we use directed length dimensions, then Vx will be dimensioned as LxT,Vy as LyT, S as Lx and DasLy. The dimensional equation becomes : Lx=(LxT)a(LyT)b(Ly)c and we may solve completely as a=1,b=-1 and c=1. The increase in deductive power gained by the use of directed length dimensions is apparent.
Which of the following is not a physical quantity
Height of a boy
Weight of a boy
Fever of a boy
Speed of a running boy
The correct Answer is:C
Step by step video, text & image solution for A physical quantity is a phyical property of a phenomenon , body, or substance , that can be quantified by measurement. The magnitude of the components of a vector are to be considered dimensionally distinct. For example , rather than an undifferentiated length unit L, we may represent length in the x direction as L_(x), and so forth. This requirement status ultimately from the requirement that each component of a physically meaningful equation (scaler or vector) must be dimensionally consistent . As as example , suppose we wish to calculate the drift S of a swimmer crossing a river flowing with velocity V_(x) and of widht D and he is swimming in direction perpendicular to the river flow with velocity V_(y) relation to river, assuming no use of directed lengths, the quantities of interest are then V_(x),V_(y) both dimensioned as (L)/(T) , S the drift and D width of river both having dimension L. with these four quantities, we may conclude tha the equation for the drift S may be written : S prop V_(x)^(a)V_(y)^(b)D^(c) Or dimensionally L=((L)/(T))^(a+b)xx(L)^(c) from which we may deduce that a+b+c=1 and a+b=0, which leaves one of these exponents undetermined. If, however, we use directed length dimensions, then V_(x) will be dimensioned as (L_(x))/(T), V_(y) as (L_(y))/(T), S as L_(x)" and " D as L_(y). The dimensional equation becomes : L_(x)=((L_(x))/(T))^(a) ((L_(y))/(T))^(b)(L_(y))^(c) and we may solve completely as a=1,b=-1 and c=1. The increase in deductive power gained by the use of directed length dimensions is apparent. Which of the following is not a physical quantity by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (O-2)Matrix Type Questions.3videos
UNIT & DIMENSIONS, BASIC MATHS AND VECTOR
- BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (J-M)1videos
UNIT & DIMENSIONS, BASIC MATHS AND VECTOR
- BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (O-2) Multiple Correct Type Questions.7videos
UNIT & DIMENSIONS, BASIC MATHS AND VECTOR
- BOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - MATHS18videos
TEST PAPERS
- BOOK - ALLENCHAPTER - WAVE OPTICSEXERCISE - Exercise 2 (Previous Year Questions)7videos
WAVE OPTICS
Similar Questions
Knowledge Check
- Question 1 - Select One
A physical quantity is a phyical property of a phenomenon , body, or substance , that can be quantified by measurement.
The magnitude of the components of a vector are to be considered dimensionally distinct. For example , rather than an undifferentiated length unit L, we may represent length in the x direction as Lx, and so forth. This requirement status ultimately from the requirement that each component of a physically meaningful equation (scaler or vector) must be dimensionally consistent . As as example , suppose we wish to calculate the drift S of a swimmer crossing a river flowing with velocity Vx and of widht D and he is swimming in direction perpendicular to the river flow with velocity Vy relation to river, assuming no use of directed lengths, the quantities of interest are then Vx,Vy both dimensioned as LT , S the drift and D width of river both having dimension L. with these four quantities, we may conclude tha the equation for the drift S may be written : S∝VaxVbyDc
Or dimensionally L=(LT)a+b×(L)c from which we may deduce that a+b+c=1 and a+b=0, which leaves one of these exponents undetermined. If, however, we use directed length dimensions, then Vx will be dimensioned as LxT,VyasLyT,SasLx and DasLy. The dimensional equation becomes : Lx=(LxT)a(LyT)b(Ly)c and we may solve completely as a=1,b=-1 and c=1. The increase in deductive power gained by the use of directed length dimensions is apparent.
From the concept of directed dimension what is the formula for a range (R) of a cannon ball when it is fired with vertical velocity component Vy and a horizontal velocity component Vx, assuming it is fired on a flat surface. [Range also depends upon acceleration due to gravity , g and k is numerical constant]AR=k(VxVy)gBR=k(Vx)2gCR=k(Vx)3VygDR=k(Vy)3Vxg - Question 2 - Select One
A physical quantity is a phyical property of a phenomenon , body, or substance , that can be quantified by measurement.
The magnitude of the components of a vector are to be considered dimensionally distinct. For example , rather than an undifferentiated length unit L, we may represent length in the x direction as Lx, and so forth. This requirement status ultimately from the requirement that each component of a physically meaningful equation (scaler or vector) must be dimensionally consistent . As as example , suppose we wish to calculate the drift S of a swimmer crossing a river flowing with velocity Vx and of widht D and he is swimming in direction perpendicular to the river flow with velocity Vy relation to river, assuming no use of directed lengths, the quantities of interest are then Vx,Vy both dimensioned as LT , S the drift and D width of river both having dimension L. with these four quantities, we may conclude tha the equation for the drift S may be written : S∝VaxVbyDc
Or dimensionally L=(LT)a+b×(L)c from which we may deduce that a+b+c=1 and a+b=0, which leaves one of these exponents undetermined. If, however, we use directed length dimensions, then Vx will be dimensioned as LxT,VyasLyT,SasLx and DasLy. The dimensional equation becomes : Lx=(LxT)a(LyT)b(Ly)c and we may solve completely as a=1,b=-1 and c=1. The increase in deductive power gained by the use of directed length dimensions is apparent.
A conveyer belt of width D is moving along x-axis with velocity V. A man moving with velocity U on the belt in the direction perpedicular to the belt's velocity with respect to belt want to cross the belt. The correct expression for the drift (S) suffered by man is given by (k is numerical costant )AS=kUDVBS=kVDUCS=kU2DV2DS=kV2DU2 - Question 3 - Select One
The component of a vector may be
Adouble its magnitude.Bequal to its magnitude.Cgreater than its magnitude.Deither greater or equal to its magnitude.
Can a rectangular component of a vector be greater than the vector itself ?
View SolutionCan any of the components of a given vector have greater magnitude than that of the vector itself ?
View SolutionWhat physical quantities may X and Y represent ?
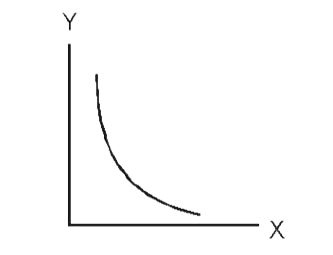 View Solution
View SolutionWhat physical quantities may X and Y represent?
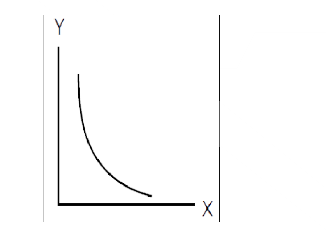 View Solution
View SolutionThe magnitude of the x-component of vector →A is 3 and the magnitude of vector →A is 5. What is the magnitude of the y-component of vector →A ?
View Solution

