An electron in a hydrogen atom is considered to be revolving around a proton with a velocity e2n in a circular orbit of radius n2me2. If I is the equivalent current, express it in terms of m, e, n.
To find the equivalent current I for an electron revolving around a proton in a hydrogen atom, we can follow these steps:
Step 1: Understand the motion of the electron
The electron is moving in a circular orbit around the proton. The velocity v of the electron is given by:
v=e2n
Step 2: Determine the radius of the orbit
The radius r of the orbit is given by:
r=n2me2
Step 3: Calculate the circumference of the orbit
The circumference C of the circular orbit can be calculated using the formula for the circumference of a circle:
C=2πr
Substituting the expression for r:
C=2π(n2me2)=2πn2me2
Step 4: Calculate the time period T for one complete revolution
The time period T is the time taken for one complete revolution, which can be calculated using the formula:
T=CircumferenceVelocity=Cv
Substituting the expressions for C and v:
T=2πn2me2e2n=2πn2me2⋅ne2=2πn3me4
Step 5: Calculate the equivalent current I
The equivalent current I can be defined as the charge passing through a point per unit time. The charge of the electron is e. Therefore, the current I is given by:
I=ChargeTime period=eT
Substituting the expression for T:
I=e2πn3me4=e⋅me42πn3=me52πn3
Final Expression
Thus, the equivalent current I in terms of m, e, and n is:
I=me52πn3
---
The electron is moving in a circular orbit around the proton. The velocity v of the electron is given by:
The radius r of the orbit is given by:
The circumference C of the circular orbit can be calculated using the formula for the circumference of a circle:
The time period T is the time taken for one complete revolution, which can be calculated using the formula:
The equivalent current I can be defined as the charge passing through a point per unit time. The charge of the electron is e. Therefore, the current I is given by:
Thus, the equivalent current I in terms of m, e, and n is:
Topper's Solved these Questions
- ELECTROSTATICS AND CURRENT ELECTRICITY BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - ELECTROSTATICS AND CURRENT ELECTRICITY EXERCISE - SHORT ANSWER QUESTIONS (3 MARKS )
23 Videos
- ELECTROSTATICS AND CURRENT ELECTRICITY BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - ELECTROSTATICS AND CURRENT ELECTRICITY EXERCISE - LONG ANSWER QUESTIONS
6 Videos
- ELECTROSTATICS AND CURRENT ELECTRICITY BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - ELECTROSTATICS AND CURRENT ELECTRICITY EXERCISE - NUMERICALS
49 Videos
- ELECTRONIC DEVICES BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - ELECTRONIC DEVICES EXERCISE - NUMERICALS
7 Videos
- SAMPLE QUESTION PAPER 2019BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - SAMPLE QUESTION PAPER 2019EXERCISE - Section C
19 Videos
Similar Questions
In the Bohr model of the hydrogen atom, in the lowest energy state the electron revolves round the proton at a speed of 2.2×106ms in a circular orbit of radius 5.3×10−11 m.
(a) What is the orbital period of the electron?
(b) If the orbiting electron is considered to be a current loop, what is the current I? (c) What is the magnetic moment of the atom due to the motion of the electron?
View SolutionIn Bohr model of hydrogen atom , the electron revolves around the nucleus in a circular orbit of radius 5.1×10−11m at a frequency of 6.8×1015 revolutions per second. Find the equivalent current at may point on the orbit of the electron
View Solution
Knowledge Check
An electron of hydrogen atoms is considered to be revolving round the proton in the circuit orbit of radius h22π2me2with velocity2πe2h the equivalent current due to circuiting charge is
A4π2me4h3B4π2me5h3C4π2m2e4h3DNone of aboveThe electron of hydrogen atom is considered to be revolving around the proton in circular orbit of radius h2me2 with velocity e2h, where h=h2π. The curret I is
A4π2me2h2B4π2me2h3C4π2m2e2h3D4π2me5h3An electron in the hydrogen atom circles around the proton with a speed of 2.18×106m/s in an orbit of radius 0.53Å . The equivalent current is
A1.048×10−2AB1.048×10−3AC1.048×10−4AD1.058×10−4A
An electron in the ground state of hydrogen atom is revolving in anti-clockwise direction in a circular orbit of radius R.

(i) The expression for the orbital magnetic moment of the electrton is ehnπm. Find n □
(ii) The atom is placed in a uniform magnetic induction B such that the normal to the plane of electron’s orbit makes an angle of 30∘ with the magnetic induction. The torque experienced by the orbiting electron is ehBnπm. Find n □
View SolutionAn electron in the ground state of hydrogen atom is revolving in anti-clockwise direction in the circular orbit of radius R as shown in figure.
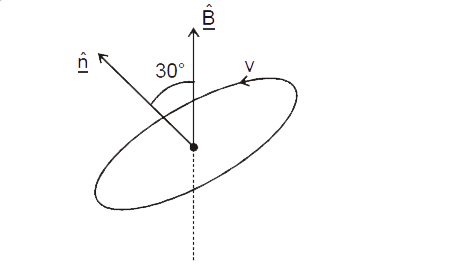
The atom is placed in a uniform magnetic induction B such that the plane normal of the electron orbit makes an angle 30∘ with the magnetic induction. Find the torque experienced by the orbiting electron.
View SolutionAn electron of charge 'e' is revolving in a circular orbit of radius r around a nucleus with speed v. The equivalent current is
View SolutionAn electron is revolving round a proton, producing a magnetic field of 16weber/m2 in a circular orbit of radius 1 Å. Its angular velocity will be
View SolutionAn electron is revolving round a proton, producing a magnetic field of 16weber/m2 in a circular orbit of radius 1 Å. Its angular velocity will be
View Solution
