A point charge of 2μC is kept fixed at the origin. Another point charge of 4μC is brought from a far point to a distance of 50cm from origin. (a) Calculate the electrostatic potential energy of the two charge system. Another charge of 11μC is brought to a point 100 cm from each of the two charges. What is the work done ?
To solve the problem step by step, we will break it down into two parts: calculating the electrostatic potential energy of the first two charges and then calculating the work done when the third charge is brought into the system.
Step 1: Calculate the Electrostatic Potential Energy of the Two Charge System
1. Identify the Charges and Distance:
- Charge q1=2μC=2×10−6C
- Charge q2=4μC=4×10−6C
- Distance r=50cm=0.5m
2. Use the Formula for Electrostatic Potential Energy:
The formula for electrostatic potential energy U between two point charges is given by:
U=14πϵ0⋅q1q2r
where ϵ0 (the permittivity of free space) is approximately 8.85×10−12C2/(N⋅m2).
3. Calculate the Potential Energy:
U=14π(8.85×10−12)⋅(2×10−6)(4×10−6)0.5
U=9×1091⋅8×10−120.5
U=9×109⋅16×10−12
U=0.144J
Step 2: Calculate the Work Done When Bringing the Third Charge
1. Identify the Third Charge and its Distance:
- Charge q3=11μC=11×10−6C
- The distance from each charge to the third charge is 100cm=1m.
2. Calculate the Final Potential Energy:
The potential energy between the third charge and the first two charges can be calculated as follows:
Uf=U13+U23
where:
- U13=14πϵ0⋅q1q3r13
- U23=14πϵ0⋅q2q3r23
U13=9×109⋅(2×10−6)(11×10−6)1
U13=9×109⋅22×10−12=0.198J
U23=9×109⋅(4×10−6)(11×10−6)1
U23=9×109⋅44×10−12=0.396J
Thus, the total final potential energy is:
Uf=0.198+0.396=0.594J
3. Calculate the Initial Potential Energy:
The initial potential energy Ui is simply the potential energy between the first two charges:
Ui=0.144J
4. Calculate the Work Done:
The work done W in bringing the third charge into the system is given by:
W=Uf−Ui
W=0.594−0.144=0.45J
Final Answers:
- The electrostatic potential energy of the two charge system is 0.144J.
- The work done in bringing the third charge into the system is 0.45J.
- Charge q1=2μC=2×10−6C
- Charge q2=4μC=4×10−6C
- Distance r=50cm=0.5m
The formula for electrostatic potential energy U between two point charges is given by:
U=14πϵ0⋅q1q2r
where ϵ0 (the permittivity of free space) is approximately 8.85×10−12C2/(N⋅m2).
U=14π(8.85×10−12)⋅(2×10−6)(4×10−6)0.5
U=9×1091⋅8×10−120.5
U=9×109⋅16×10−12
U=0.144J
- Charge q3=11μC=11×10−6C
- The distance from each charge to the third charge is 100cm=1m.
The potential energy between the third charge and the first two charges can be calculated as follows:
Uf=U13+U23
where:
- U13=14πϵ0⋅q1q3r13
- U23=14πϵ0⋅q2q3r23
U13=9×109⋅22×10−12=0.198J
U23=9×109⋅44×10−12=0.396J
Uf=0.198+0.396=0.594J
The initial potential energy Ui is simply the potential energy between the first two charges:
Ui=0.144J
The work done W in bringing the third charge into the system is given by:
W=Uf−Ui
W=0.594−0.144=0.45J
- The electrostatic potential energy of the two charge system is 0.144J.
- The work done in bringing the third charge into the system is 0.45J.
Topper's Solved these Questions
- ELECTROSTATICS AND CURRENT ELECTRICITY BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - ELECTROSTATICS AND CURRENT ELECTRICITY EXERCISE - LONG ANSWER QUESTIONS
6 Videos
- ELECTRONIC DEVICES BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - ELECTRONIC DEVICES EXERCISE - NUMERICALS
7 Videos
- SAMPLE QUESTION PAPER 2019BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - SAMPLE QUESTION PAPER 2019EXERCISE - Section C
19 Videos
Similar Questions
Two point charges, q1=10×10−8Candq2=−2×10−8C, are separated by a distance of 60 cm in air.
Also calculate the electrostatic potential energy of the system.
View SolutionTwo point charges 10μCand−10μC are separated by a distance of 40 cm in air.
Calculate the electrostatic potential energy of the system, assuming the zero of the potential energy to be at infinity.
View Solution
Knowledge Check
The distance of point (−4,5) from origin is :
A1B9C√41DNone of these
Two point charges q1, and q2 are kept at a distance of r12 in air. Deduce the expression for the electrostatic potential energy of this system.
View SolutionA point charge of 0.01 μC is placed at the origin. Calculate the electric field at another point charge of 0.05 μC placed at (0 m, 5 m).
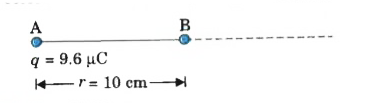
View SolutionA point charge of 9.6 μC is placed at a point A. Point B is at a distance of 10 cm from A. (i) Calculate electric potential at point B due to charge at A. (ii) If a point charge of 3 nC is brought from infinity to the point B, then calculate work done by the external agent in this process assuming motion of charge to be slow.
View SolutionWhen a particle of charge 10 μC is brought from infinity to a point P, 2.0 mJ of work is done by the external forces. What is the potential at P?
View SolutionThe distance of the point P(2,4) from the origin is :
View SolutionTwo point charges , each of 1μC ,are separated from each other by a distance of 10 cm in air . Electrostatic force acting between them is ____________
View SolutionA point charge q is placed at the origin . How does the electric field due to the charge very with distance r from the origin ?
View Solution
