The knowledge of elasticity useful in selecting metal ropes show its use, in cranes for lifting heavy loads, when rope of steel is used (Elastic limit 30×107Nm−2) if load of 100000 kg is to be lifted.
What should be the radius of steel rope ? What should we do to increase flexibility of such wire ?
The ultimate stress should not exceed elastic limit of steel (30×107N/m2)
U=FA=Mgπr2=105×9.8πr2=30×107
∴R=3.2 cm
So to lift a bad of 104 kg, crane is designed to withstand 105 kg. To impart flexibility the rope is made of large number of thin wires braided.
Topper's Solved these Questions
- PROPERTIES OF MATTERBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - PROPERTIES OF MATTEREXERCISE - Long Answer Type Questions (5 Marks)
1 Videos
- PROPERTIES OF MATTERBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - PROPERTIES OF MATTEREXERCISE - NUMERICALS
23 Videos
- PROPERTIES OF MATTERBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - PROPERTIES OF MATTEREXERCISE - Short Answer Type Questions (2 Marks)
25 Videos
- NEWTON'S LAWS OF MOTIONBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - Laws Of Motion
20 Videos
- ROTATIONAL MOTION BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - ROTATIONAL MOTION EXERCISE - MULTIPLE CHOICE QUESTIONS
20 Videos
Similar Questions
The knowledge of elasticity useful in selecting metal ropes show its use, in cranes for lifting heavy loads, when rope of steel is used (Elastic limit 30×107Nm−2) if load of 100000 kg is to be lifted.
What should be the radius of steel rope ? What should we do to increase flexibility of such wire ?
View SolutionHow is the knowledge of elasticity useful in selecting metal ropes used in cranes for lifting heavy loads ?
View Solution
Knowledge Check
To lift a load by a metallic rope, its radius of cross-section should be
A≥1mmB≤1cmC≥1cmD≥2cmTwo blocks of masses 1kg and 2kg are connected by a metal wire going over a smooth pulley as shown in figure.
The breaking stress of the metal is (40/3π)×106N/m2. If g=10ms−2, then what should be the minimum radius of the wire used if it is not to break?
 A0.5 mmB1 mmC1.5 mmD2 mm
A0.5 mmB1 mmC1.5 mmD2 mmTwo blocks of masses 1kg and 2kg are connected by a metal wire goijng over a smooth pulley as shown in figure.
The breaking stress of the metal is (40/3π)×106N/m2. If g=10ms−12, then what should be the minimum radlus of the wire used if it is not to break?
 A0.5mmB1mmC1.5mmD2mm
A0.5mmB1mmC1.5mmD2mm
Explain how is the knowledge of elasticity useful in selecting metal ropes used in cranes for lifting heavy loads.
View SolutionTwo blocks of masses 1kg and 2kg are connected by a metal wire going over a smooth pulley as shown in figure.
The breaking stress of the metal is (40/3π)×106N/m2. If g=10ms−2, then what should be the minimum radius of the wire used if it is not to break?

View SolutionTwo blocks of masses 2 kg and 3kg are connected by a metal wire going over a smoother pulley as shown in figure. The breaking stress of the steel is 2×109Nm−2. What would be the minimum radius of the wire used if it not to break ? Take ,g=10ms−2
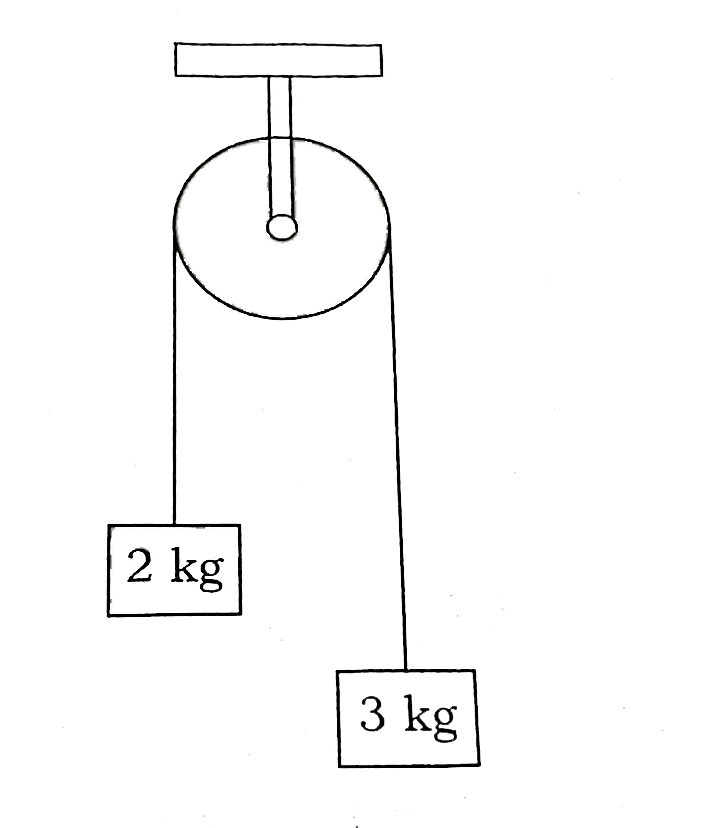
View SolutionTwo blocks of masses 2 kg and 3kg are connected by a metal wire going over a smoother pulley as shown in figure. The breaking stress of the steel is 2×109Nm−2. What would be the minimum radius of the wire used if it not to break ? Take ,g=10ms−2

View SolutionThe area of cross section of a steel rope used for lifting should be greater than or equal to
View Solution
