Show that for a small oscillations the motion of a simple pendulum is simple harmonic. Derive an expression of its time period.
To show that the motion of a simple pendulum is simple harmonic for small oscillations and derive an expression for its time period, we can follow these steps:
Step 1: Understanding the Pendulum Setup
A simple pendulum consists of a mass (bob) attached to a string of length L that swings back and forth about a fixed point (the pivot). When the pendulum is displaced from its equilibrium position by a small angle θ, it experiences a restoring force that attempts to bring it back to the equilibrium position.
Step 2: Analyzing Forces Acting on the Bob
When the pendulum is displaced to an angle θ, the weight of the bob (mg) can be resolved into two components:
- A component along the direction of the string, mgcosθ (which balances the tension).
- A component perpendicular to the string, mgsinθ (which acts as the restoring force).
Step 3: Establishing the Restoring Force
The restoring force F acting on the bob is given by:
F=−mgsinθ
The negative sign indicates that the force acts in the opposite direction of the displacement.
Step 4: Small Angle Approximation
For small angles (in radians), we can use the approximation:
sinθ≈θ
Thus, the restoring force can be rewritten as:
F≈−mgθ
Step 5: Relating Force to Torque
The torque τ about the pivot point due to the restoring force is given by:
τ=−mgLsinθ
Using the small angle approximation:
τ≈−mgLθ
Step 6: Using Newton's Second Law for Rotation
According to Newton's second law for rotation, torque is related to angular acceleration (α) by:
τ=Iα
where I is the moment of inertia of the bob about the pivot. For a point mass at a distance L:
I=mL2
Thus, we have:
−mgLθ=mL2α
Step 7: Relating Angular Acceleration to Angular Displacement
The angular acceleration α can be expressed as:
α=d2θdt2
Substituting this into the torque equation gives:
−mgLθ=mL2d2θdt2
Dividing through by mL2:
d2θdt2+gLθ=0
Step 8: Identifying Simple Harmonic Motion
The equation:
d2θdt2+gLθ=0
is the standard form of the equation for simple harmonic motion, where:
ω2=gL
Thus, the motion is simple harmonic.
Step 9: Deriving the Time Period
The time period T of simple harmonic motion is given by:
T=2π1ω
Substituting ω=√gL:
T=2π√Lg
Final Expression
The time period of a simple pendulum undergoing small oscillations is:
T=2π√Lg
A simple pendulum consists of a mass (bob) attached to a string of length L that swings back and forth about a fixed point (the pivot). When the pendulum is displaced from its equilibrium position by a small angle θ, it experiences a restoring force that attempts to bring it back to the equilibrium position.
When the pendulum is displaced to an angle θ, the weight of the bob (mg) can be resolved into two components:
- A component along the direction of the string, mgcosθ (which balances the tension).
- A component perpendicular to the string, mgsinθ (which acts as the restoring force).
The restoring force F acting on the bob is given by:
F=−mgsinθ
The negative sign indicates that the force acts in the opposite direction of the displacement.
For small angles (in radians), we can use the approximation:
sinθ≈θ
Thus, the restoring force can be rewritten as:
F≈−mgθ
The torque τ about the pivot point due to the restoring force is given by:
τ=−mgLsinθ
Using the small angle approximation:
τ≈−mgLθ
According to Newton's second law for rotation, torque is related to angular acceleration (α) by:
τ=Iα
where I is the moment of inertia of the bob about the pivot. For a point mass at a distance L:
I=mL2
Thus, we have:
−mgLθ=mL2α
The angular acceleration α can be expressed as:
α=d2θdt2
Substituting this into the torque equation gives:
−mgLθ=mL2d2θdt2
Dividing through by mL2:
d2θdt2+gLθ=0
The equation:
d2θdt2+gLθ=0
is the standard form of the equation for simple harmonic motion, where:
ω2=gL
Thus, the motion is simple harmonic.
The time period T of simple harmonic motion is given by:
T=2π1ω
Substituting ω=√gL:
T=2π√Lg
The time period of a simple pendulum undergoing small oscillations is:
T=2π√Lg
Topper's Solved these Questions
- MECHANICAL WAVESBook:CBSE COMPLEMENTARY MATERIALChapter:MECHANICAL WAVESExercise:LONG QUESTIONS
Explore 1 Video
- MECHANICAL WAVESBook:CBSE COMPLEMENTARY MATERIALChapter:MECHANICAL WAVESExercise:NUMERICALS
Explore 22 Videos
- MECHANICAL WAVESBook:CBSE COMPLEMENTARY MATERIALChapter:MECHANICAL WAVESExercise:TWO MARK QUESTIONS
Explore 21 Videos
- KINETIC THEORY OF GASESBook:CBSE COMPLEMENTARY MATERIALChapter:KINETIC THEORY OF GASESExercise:Objective question
Explore 20 Videos
- NEWTON'S LAWS OF MOTIONBook:CBSE COMPLEMENTARY MATERIALChapter:NEWTON'S LAWS OF MOTIONExercise:Laws Of Motion
Explore 20 Videos
Similar Questions
Knowledge Check
Time period of simple pendulum is
AT=2π√lgBT=2π√glCT=√2πlgDT=12π√glTime period of simple pendulum increase with
Aincrease in value of gBincrease in amplitudeCdecrease in value of gDdecrease in amplitudeThe time period of a simple pendulum in a satellite is
ASame on the earth,BZeroCInfiniteDNone of these.
When will the motion of a simple pendulum be simple harmonic?
View SolutionWhat is the time period of a simple pendulum ?
View SolutionShow that the motion of simple pendulum is simple harmonic and hence derive an equation for its time period.What is Seconds pendulum?
View SolutionWhat forces keep the simple pendulum in simple harmonic motion?
View SolutionThe oscillation of a simple pendulum is graphically represented as follows. Determine the
(a) time period (b) frequency (c) amplitude
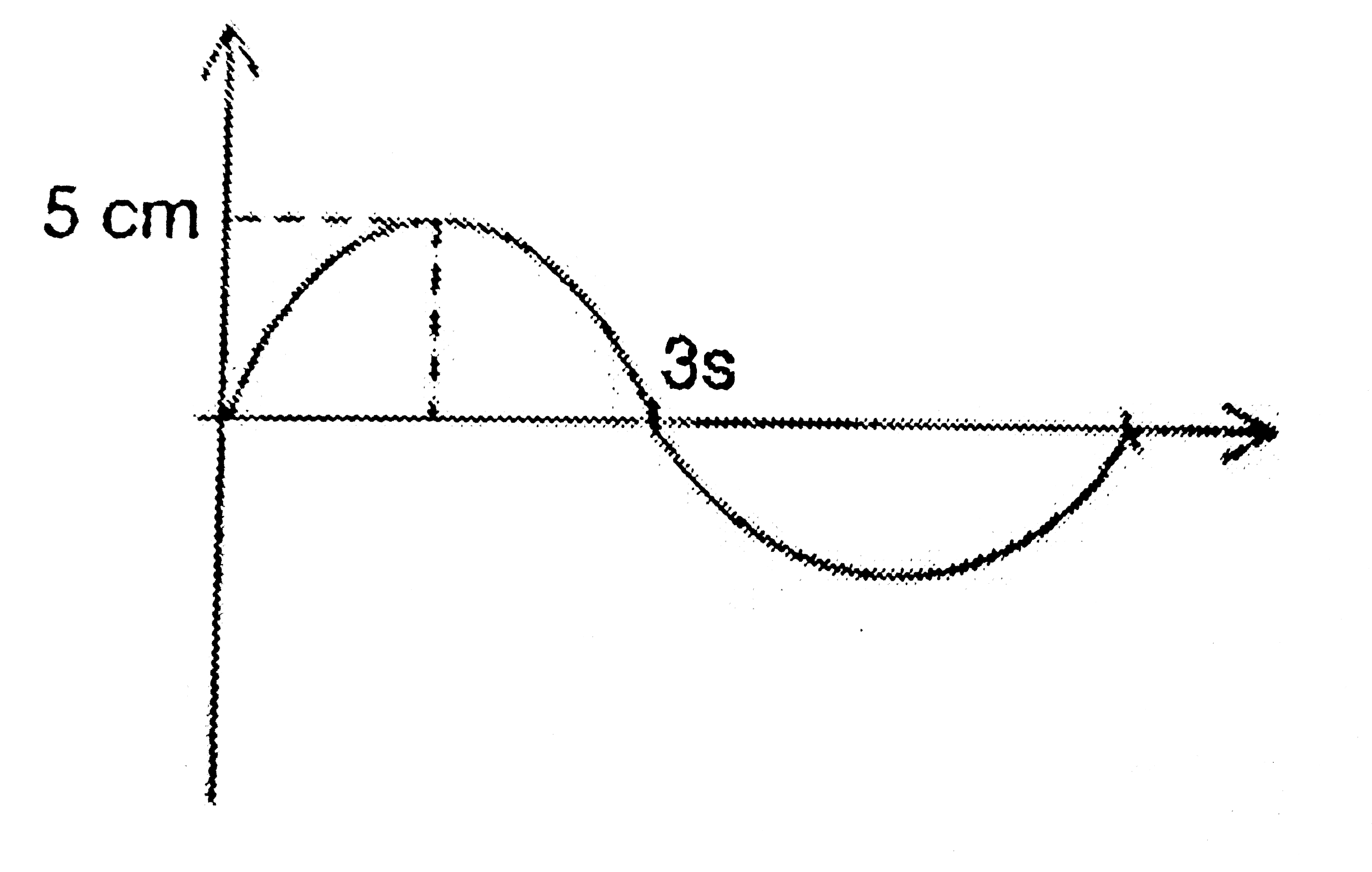
View Solution
