ab−mn+an−bm = ?
(a−b)(m−n)
(a−m)(b+n)
(a−n)(m+b)
(m−a)(n−b)
The correct Answer is:B
To factor the expression ab−mn+an−bm, we can follow these steps:
1. Rearrange the expression:
We can rearrange the terms to group them in a way that makes factoring easier:
ab+an−mn−bm
2. Group the terms:
Now, we can group the first two terms and the last two terms:
(ab+an)+(−mn−bm)
3. Factor out the common factors:
- From the first group ab+an, we can factor out a:
a(b+n)
- From the second group −mn−bm, we can factor out −m:
−m(n+b)
Now, we rewrite the expression:
a(b+n)−m(n+b)
4. Notice that (n+b) can be rewritten:
Since (n+b) is the same as (b+n), we can rewrite the expression as:
a(b+n)−m(b+n)
5. Factor out the common binomial factor:
Now, we can factor out the common binomial (b+n):
(b+n)(a−m)
Thus, the final factored form of the expression ab−mn+an−bm is:
(b+n)(a−m)
We can rearrange the terms to group them in a way that makes factoring easier:
ab+an−mn−bm
Now, we can group the first two terms and the last two terms:
(ab+an)+(−mn−bm)
- From the first group ab+an, we can factor out a:
a(b+n)
- From the second group −mn−bm, we can factor out −m:
−m(n+b)
a(b+n)−m(n+b)
Since (n+b) is the same as (b+n), we can rewrite the expression as:
a(b+n)−m(b+n)
Now, we can factor out the common binomial (b+n):
(b+n)(a−m)
(b+n)(a−m)
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - FACTORISATION EXERCISE - EXERCISE 7D42videos
FACTORISATION
- BOOK - RS AGGARWALCHAPTER - EXPONENTS EXERCISE - TEST PAPER-218videos
EXPONENTS
- BOOK - RS AGGARWALCHAPTER - INTRODUCTION TO COORDINATE GEOMETRYEXERCISE - EXERCISE B (OBJECTIVE QUESTIONS)7videos
INTRODUCTION TO COORDINATE GEOMETRY
Similar Questions
Knowledge Check
- Question 1 - Select One
In the given figure, AB = 30 cm and CD = 24 cm. What is the value (in cm) of MN?
 A18B9C12D15
A18B9C12D15 - Question 2 - Select One
If the lengths of the sides AB, BC and CA of a triangle ABC are 10 cm, 8 cm and 6 cm respectively and if M is the mid-point of BC and MN || AB to cut AC at N, then the area of the trapezium ABMN is equal to
A(a) 18 sq. cmB(b) 20 sq. cmC(c) 12 sq. cmD(d) 16 sq. cm - Question 3 - Select One
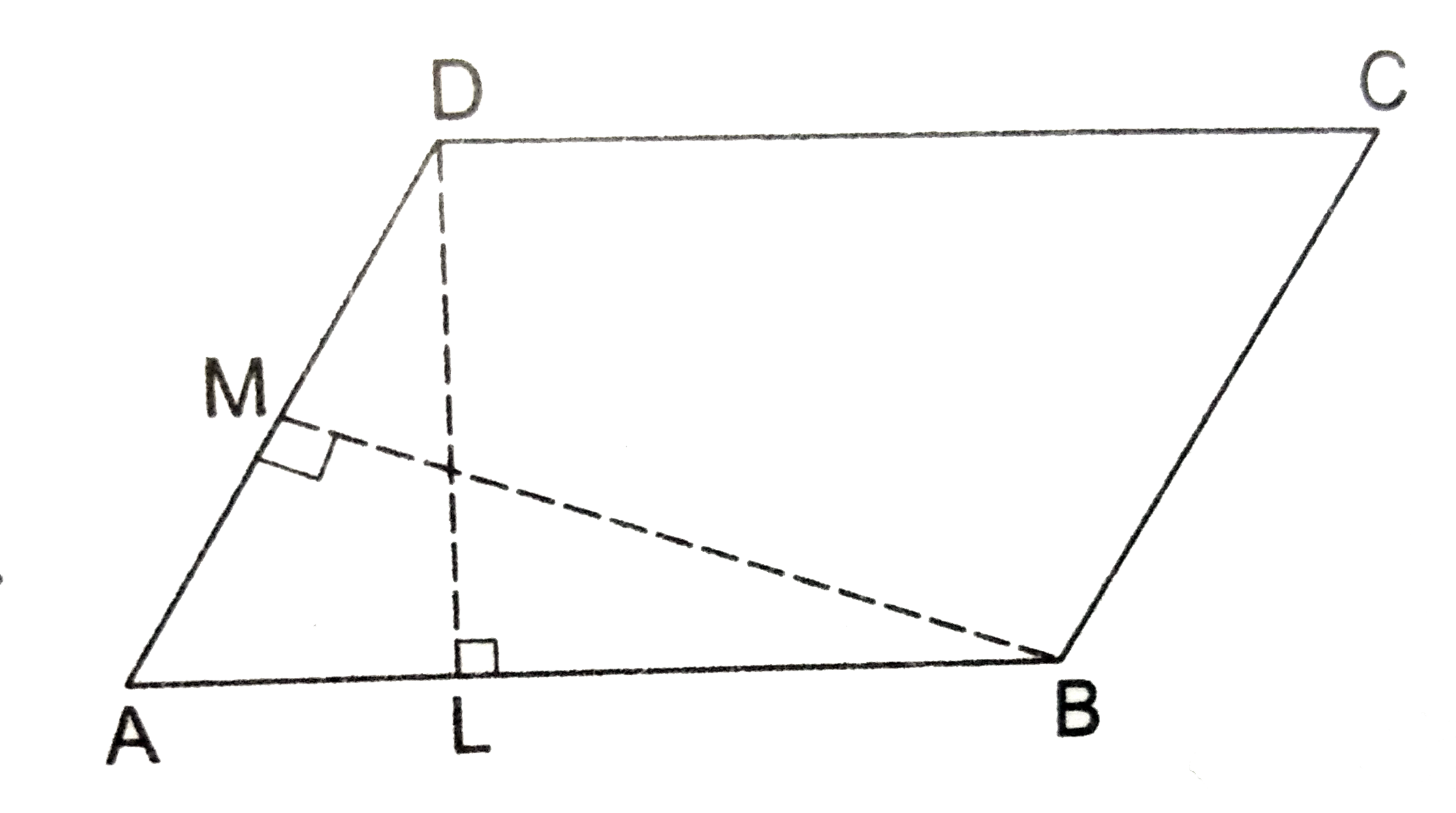
In the given figure, ABCD is a trapezium such that AL⊥DCandBM⊥DC. If AB=7cm,BC=AD=5cm and AL=BM=4cm then ar(trap.ABCD)=?
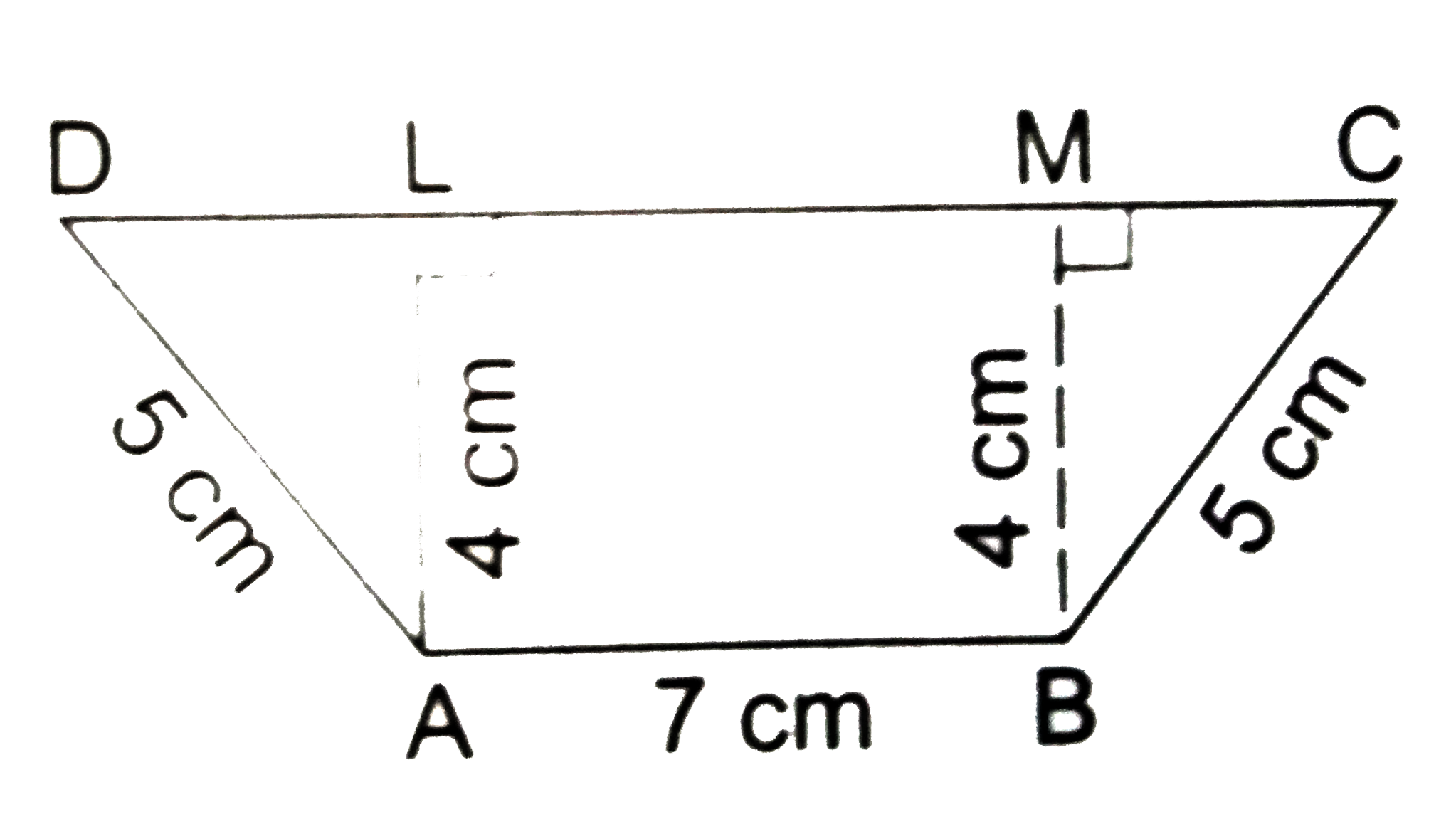 A24cm2B40cm2C55cm2D27.5cm2
A24cm2B40cm2C55cm2D27.5cm2
Add:
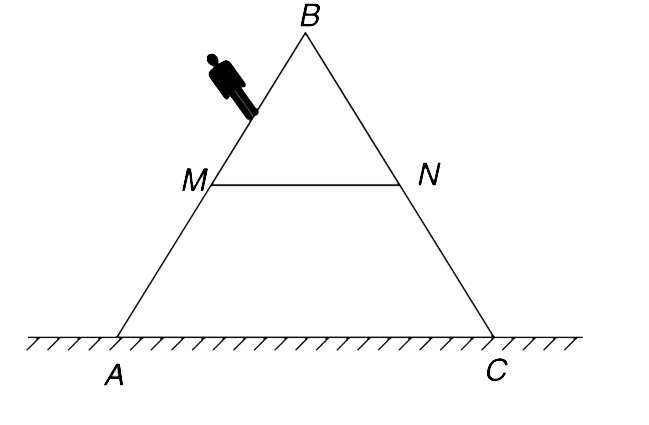
−7mn+5,12mn+2,9mn−8,−2mn−3View SolutionThe ladder shown in the figure is light and stands on a frictionless horizontal surface. Arms AB and BC are of equal length and M and N are their mid points. Length of MN is half that of AB. A man of mass M is standing at the midpoint of BM. Find the tension in the mass less rod MN. Consider the man to be a point object.
 View Solution
View Solution∠ABC=90∘ and BM is a median AB=8cm and BC=6cm. Then, length BM is equal to
View SolutionA semi-circle has been drawn on AB as a diameter and two chords ALandBM have been draw there in which intersect each other a P. Prove that AB2=AL−AP+BM−BP.
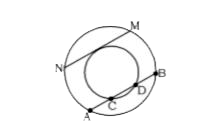
View SolutionIt is given that in △ABC, M is midpoint of AC, circle of center B cuts AB and BC of D & E, BM cuts the chord DE at G. Here AB = 12, DG = 5, BC = 15, Find GE = ?
 View Solution
View Solution