Ten cards are numbered as 1,2,3,4,5………….10 respectively. They are kept in a box and mixed throughly. One card is chosen at random from the box. What is the probability of (i) getting the number 8? (ii) getting a number less than 5? (iii) getting a number greater than 4? (iv) getting a 1-digit number?
The correct Answer is:(i) 110 (ii) 25 (iii) 35 (iv) 910
To solve the problem step by step, we will calculate the probability for each part of the question.
Given:
- Total cards = 10 (numbered 1 to 10)
- Sample space (S) = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
Probability Formula:
The probability (P) of an event is given by the formula:
P(E)=Number of favorable outcomesTotal number of outcomes
Part (i): Probability of getting the number 8
1. Identify the favorable outcome: The only favorable outcome for this event is the card numbered 8. So, the number of favorable outcomes = 1.
2. Total outcomes: There are 10 cards in total.
3. Calculate the probability:
P(getting 8)=110
Part (ii): Probability of getting a number less than 5
1. Identify the favorable outcomes: The numbers less than 5 are {1, 2, 3, 4}. So, the number of favorable outcomes = 4.
2. Total outcomes: There are still 10 cards in total.
3. Calculate the probability:
P(getting a number less than 5)=410=25
Part (iii): Probability of getting a number greater than 4
1. Identify the favorable outcomes: The numbers greater than 4 are {5, 6, 7, 8, 9, 10}. So, the number of favorable outcomes = 6.
2. Total outcomes: There are still 10 cards in total.
3. Calculate the probability:
P(getting a number greater than 4)=610=35
Part (iv): Probability of getting a 1-digit number
1. Identify the favorable outcomes: All the cards numbered from 1 to 9 are 1-digit numbers. So, the favorable outcomes are {1, 2, 3, 4, 5, 6, 7, 8, 9}. Thus, the number of favorable outcomes = 9.
2. Total outcomes: There are still 10 cards in total.
3. Calculate the probability:
P(getting a 1-digit number)=910
Summary of Answers:
- (i) Probability of getting the number 8: 110
- (ii) Probability of getting a number less than 5: 25
- (iii) Probability of getting a number greater than 4: 35
- (iv) Probability of getting a 1-digit number: 910
- Total cards = 10 (numbered 1 to 10)
- Sample space (S) = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
The probability (P) of an event is given by the formula:
P(E)=Number of favorable outcomesTotal number of outcomes
1. Identify the favorable outcome: The only favorable outcome for this event is the card numbered 8. So, the number of favorable outcomes = 1.
2. Total outcomes: There are 10 cards in total.
3. Calculate the probability:
P(getting 8)=110
1. Identify the favorable outcomes: The numbers less than 5 are {1, 2, 3, 4}. So, the number of favorable outcomes = 4.
2. Total outcomes: There are still 10 cards in total.
3. Calculate the probability:
P(getting a number less than 5)=410=25
1. Identify the favorable outcomes: The numbers greater than 4 are {5, 6, 7, 8, 9, 10}. So, the number of favorable outcomes = 6.
2. Total outcomes: There are still 10 cards in total.
3. Calculate the probability:
P(getting a number greater than 4)=610=35
1. Identify the favorable outcomes: All the cards numbered from 1 to 9 are 1-digit numbers. So, the favorable outcomes are {1, 2, 3, 4, 5, 6, 7, 8, 9}. Thus, the number of favorable outcomes = 9.
2. Total outcomes: There are still 10 cards in total.
3. Calculate the probability:
P(getting a 1-digit number)=910
- (i) Probability of getting the number 8: 110
- (ii) Probability of getting a number less than 5: 25
- (iii) Probability of getting a number greater than 4: 35
- (iv) Probability of getting a 1-digit number: 910
Topper's Solved these Questions
- PROBABILITYBOOK - RS AGGARWALCHAPTER - PROBABILITYEXERCISE - EXERCISE 25A
15 Videos
- PROBABILITYBOOK - RS AGGARWALCHAPTER - PROBABILITYEXERCISE - EXERCISE 25B OBJECTIVE QUESTIONS
8 Videos
- POLYGONSBOOK - RS AGGARWALCHAPTER - POLYGONSEXERCISE - EXERCISE 14B
14 Videos
- PROFIT AND LOSS BOOK - RS AGGARWALCHAPTER - PROFIT AND LOSS EXERCISE - TEST PAPER - 10 (D) (Write T for true and F for false for each of the following:)
4 Videos
Similar Questions
9 cards are numbered as 1,2,3,4,5,6,7,8.9. They are kept in a box and mixed thoroughly. One card is chosen at random. What is the probability of getting a prime number ?
View SolutionNumbers 1 to 10 are written on ten separate slips (one number on one slip), kept in a box and mixed well. One slip is chosen from the box without looking into it. What is the probability of .(i) getting a number 6?(ii) getting a number less than 6?(iii) getting a number greater than 6?(iv) getting a 1-digit number?
View Solution
Knowledge Check
8 cards are numbered as 1,2,3,4,5,6,7,8 respectively. They are kept in a box and mixed thoroughly. One card is chosen at random. What is the probability of getting a number less than 4?
A12B34C38D35Cards, each marked with one of the numbers 6,7,8,…,15, are placed in a box and mixed thoroughly. One card is drawn at random from the box. What is the probability of getting a card with number less than 10?
A45B35C15D25
Cards each marked with one of the numbers 4, 5, 6, ......, 20 are placed in a box and mixed thoroughly. One card is drawn at random from the box. What is the probability of getting an even number?
View SolutionA die is thrown. What is the probability of getting (i) a prime number?
(ii) a number greater than 4? (ii) a number not greater than 5?
View Solution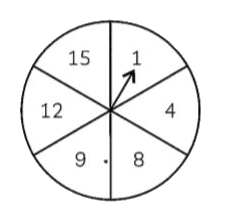
What is the probability of getting a number greater than 5 on the spinner?
View SolutionA die is tossed once. What is the probability of getting
(i) the number 4 ? (ii) an even number ?
(iii) a number less than 5 ? (iv) a number greater than 4 ?
(v) the number 8 ? (iv) a number less than 8 ?
View SolutionCards marked with numbers 3,4,5……50 are placed in a box and mixed throughly. A card is drawn at random from the box, find the probability that the selected card bears a perfect square number.
View Solution17 cards numbered 1,2,3,4, ….., 17 are put in a box and mixed thoroughly. A card is drawn at random from the box. Find the probability that the card drawn bears (i) an odd number (ii) a number divisible by 5.
View Solution
