(a) Define Photoelectric effect ? Mention its one practical application in daily life.
(b) Electrons are emitted with zero velocity from a mental surface when it is exposed to radiation of wavelength 6800 Å. Calculate thresholds freqency (Vo) and work function (Wo) of the mental.
The correct Answer is:vo=4.41×1014s−1Wo=2.92×10−19 J
Step-by-Step Solution
1. Definition of Photoelectric Effect:
- The photoelectric effect is a phenomenon where electrons are emitted from a material (usually a metal) when it absorbs electromagnetic radiation, such as light. When light of sufficient energy strikes the surface of the metal, electrons absorb this energy and are ejected from the surface.
2. Practical Application:
- One practical application of the photoelectric effect in daily life is in solar panels. In solar panels, sunlight strikes the surface, causing electrons to be emitted. This movement of electrons generates an electric current, which can be harnessed for power.
(b) Calculation of Threshold Frequency (Vo) and Work Function (Wo)
1. Given Data:
- Wavelength (λ) = 6800 Å = \(6800 \times 10^{-10}\) m
2. Calculate the Energy (E):
- The energy of the emitted electrons can be calculated using the formula:
\(
E = \frac{hc}{\lambda}
\)
- Where:
- \(h\) (Planck's constant) = \(6.626 \times 10^{-34} \, \text{J s}\)
- \(c\) (speed of light) = \(3 \times 10^8 \, \text{m/s}\)
- Substituting the values:
\(
E = \frac{(6.626 \times 10^{-34} \, \text{J s}) \times (3 \times 10^8 \, \text{m/s})}{6800 \times 10^{-10} \, \text{m}}
\)
- Calculating:
\(
E \approx 2.923 \times 10^{-19} \, \text{J}
\)
3. Determine the Work Function (W_o):
- Since electrons are emitted with zero velocity, the work function \(W_o\) is equal to the energy calculated:
\(
W_o = E = 2.923 \times 10^{-19} \, \text{J}
\)
4. Calculate the Threshold Frequency (V_o):
- The threshold frequency can be calculated using the formula:
\(
W_o = h V_o
\)
- Rearranging gives:
\(
V_o = \frac{W_o}{h}
\)
- Substituting the values:
\(
V_o = \frac{2.923 \times 10^{-19} \, \text{J}}{6.626 \times 10^{-34} \, \text{J s}} \approx 4.414 \times 10^{14} \, \text{s}^{-1}
\)
Final Answers:
- Photoelectric Effect: A phenomenon where electrons are emitted from a material when it absorbs electromagnetic radiation.
- Practical Application: Solar panels.
- Threshold Frequency (V_o): \(4.414 \times 10^{14} \, \text{s}^{-1}\)
- Work Function (W_o): \(2.923 \times 10^{-19} \, \text{J}\)
- The photoelectric effect is a phenomenon where electrons are emitted from a material (usually a metal) when it absorbs electromagnetic radiation, such as light. When light of sufficient energy strikes the surface of the metal, electrons absorb this energy and are ejected from the surface.
- One practical application of the photoelectric effect in daily life is in solar panels. In solar panels, sunlight strikes the surface, causing electrons to be emitted. This movement of electrons generates an electric current, which can be harnessed for power.
- Wavelength (λ) = 6800 Å = \(6800 \times 10^{-10}\) m
- The energy of the emitted electrons can be calculated using the formula:
\(
E = \frac{hc}{\lambda}
\)
- Where:
- \(h\) (Planck's constant) = \(6.626 \times 10^{-34} \, \text{J s}\)
- \(c\) (speed of light) = \(3 \times 10^8 \, \text{m/s}\)
- Substituting the values:
\(
E = \frac{(6.626 \times 10^{-34} \, \text{J s}) \times (3 \times 10^8 \, \text{m/s})}{6800 \times 10^{-10} \, \text{m}}
\)
- Calculating:
\(
E \approx 2.923 \times 10^{-19} \, \text{J}
\)
- Since electrons are emitted with zero velocity, the work function \(W_o\) is equal to the energy calculated:
\(
W_o = E = 2.923 \times 10^{-19} \, \text{J}
\)
- The threshold frequency can be calculated using the formula:
\(
W_o = h V_o
\)
- Rearranging gives:
\(
V_o = \frac{W_o}{h}
\)
- Substituting the values:
\(
V_o = \frac{2.923 \times 10^{-19} \, \text{J}}{6.626 \times 10^{-34} \, \text{J s}} \approx 4.414 \times 10^{14} \, \text{s}^{-1}
\)
- Photoelectric Effect: A phenomenon where electrons are emitted from a material when it absorbs electromagnetic radiation.
- Practical Application: Solar panels.
- Threshold Frequency (V_o): \(4.414 \times 10^{14} \, \text{s}^{-1}\)
- Work Function (W_o): \(2.923 \times 10^{-19} \, \text{J}\)
Topper's Solved these Questions
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - STRUCTURE OF ATOMEXERCISE - UNIT TEST8videos
STRUCTURE OF ATOM
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - STRUCTURE OF ATOMEXERCISE - 3-MARKS QUESTIONS18videos
STRUCTURE OF ATOM
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - STATES OF MATTER : GASES, LIQUIDS AND SOLIDSEXERCISE - HOTS QUESTIONS4videos
STATES OF MATTER : GASES, LIQUIDS AND SOLIDS
Similar Questions
Electrons are emitted with zero velocity from a metal surface when it is exposed to radiation of wavelength 6800 Å . Calculate threshold frequency (v0) and work function (W0) of the metal.
View SolutionElectrons are emitted with zero velocity from a metal surface when it is exposed to radiation of wavelength 6800 Å . Calculate threshold frequency (v0) and work function (W0) of the metal.
View Solution
Knowledge Check
- Question 1 - Select One
The velocity of the most energetic electrons emitted from a metallic surface is doubled when the frequecy v of incident radiation is double. The work function of this metal is
AZeroBhv/3Chv/2D2hv/3
The photoelectric threshold wavelength for tungsten is 2400Å. Determine the energy of the electrons ejected from its surface when exposed to ultraviolet radiations of wavelength 1200Å.
View SolutionIn an experiment on photoelectic effect, the graph between maximum kinetic energy (Kmax) and frequency of emitted photoelectron from metal surface is found to be a straight line as shown in fig. Calculate
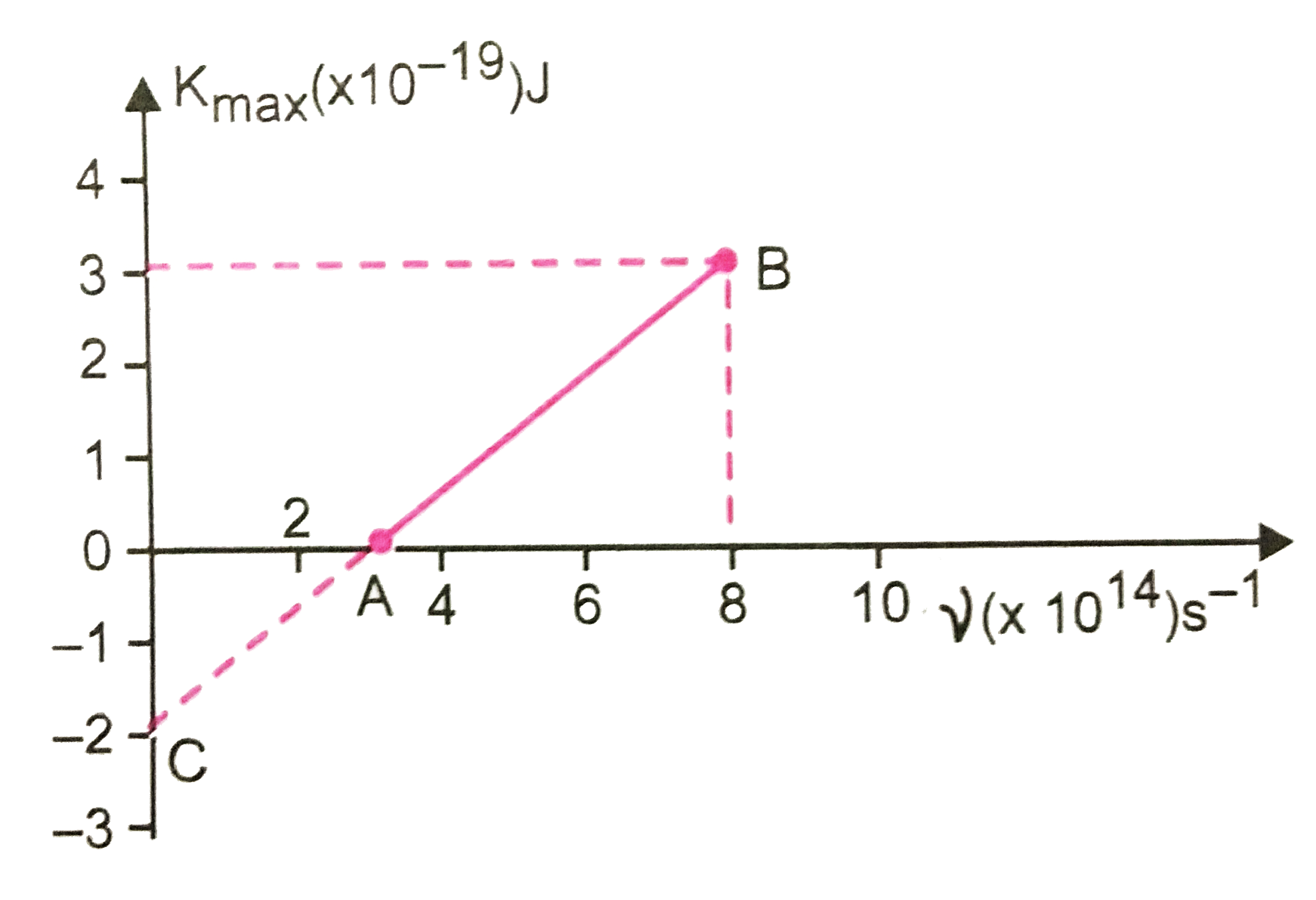
(a) thereshold frequency.
(b) work function of metal in electron volt.
(c) Planck's constant and
maximum kinetic energy of the emitted electron by light of frequency v=8×1014s−1.View SolutionCalculate the threshold freqency of the metalfrom the photoelectronsare emitted with zero velocity when exposed to radiation of wavelength 6800 Å
Hint :KE=12mv2
hv=hv0+KE,KE=0
v=cλView SolutionDerive an expression for the total energy of electron in nth Bohr orbit. Hence show that energy of the electron is inversely proportional to the square of principal quantum number. Also define binding energy.
The photoelectric threshold wavelength of a metal is is 230nm. Determine the maximum kinetic energy in joule and in eV of the ejected electron for the metal surface when it is exposed to a radiation of wavelength 180nm.
[Plank's constant: h=6.63×10−34Js, Velocity of light: c=3×108m/s]View SolutionIn the study of a photoelectric effect the graph between the stopping potential V and frequency v of the incident radiation on two different metals P and Q is shown in fig.
(i) which one of two metals have higher threshold frequency
(ii) Determine the work function of the metal which has greater value
(iii) Find the maximum kinetic energy of electron emitted by light of frequency 8×1014Hz for this metal.
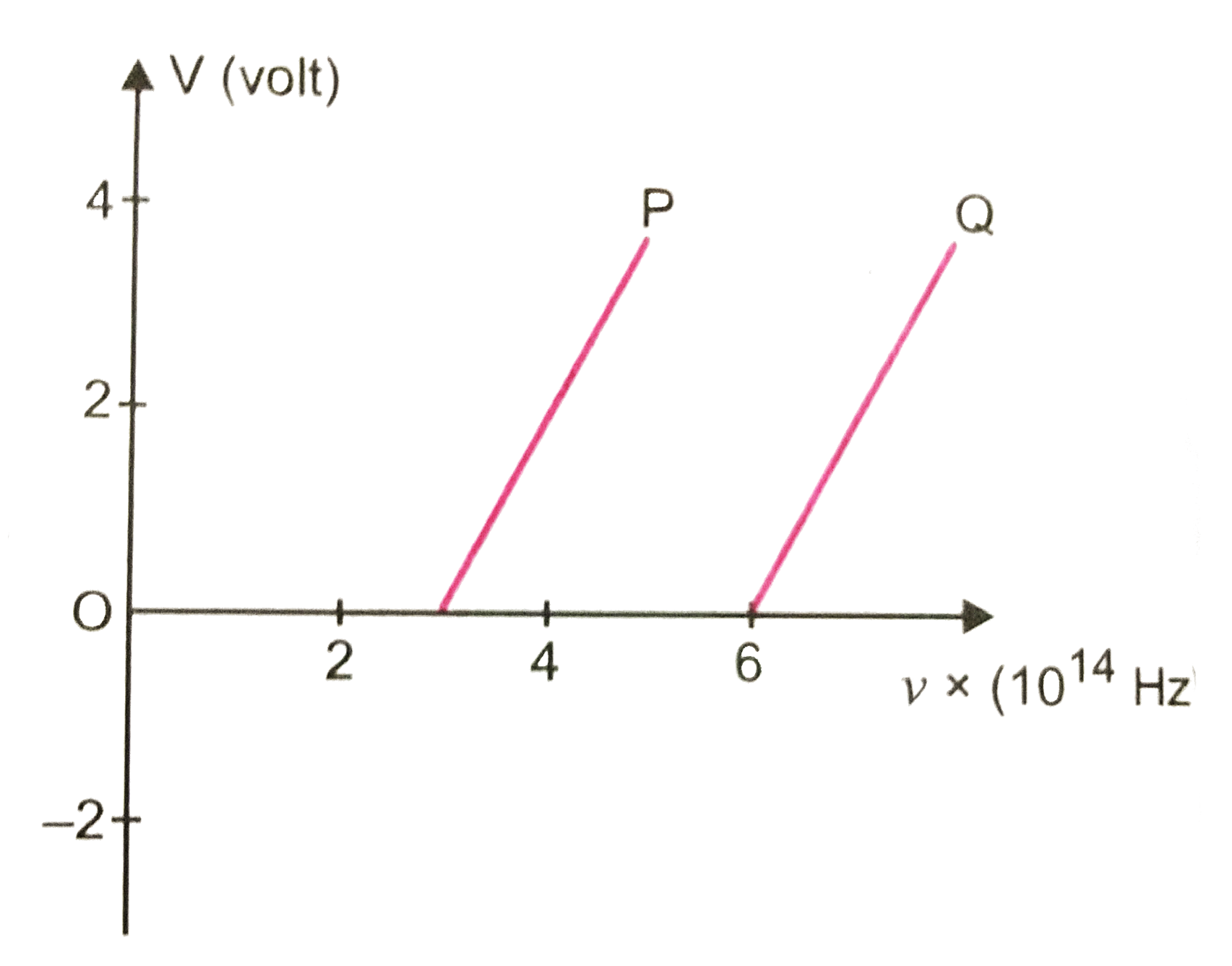 View Solution
View Solution(a) Write Einstein's photoelectric equation and mention which important features in photo-electric effect can be explained with the help of this equation.
(b) The maximum kinetic energy of the photoelectrons gets doubled when the wavelength of light incident on the surface changes from λ1 to λ2. Derive the expressions for the threshold wavelength λ0 and work function fo rthe metal surface.View Solution(a) Photoelectric threshold of metallic silver is λ=3800Å. Ultravilolet light of λ=260 nm is incident on silver surface. Calculate :
(i) the value of work function in joule and eV
Kmax of the emitted photoelectrons
(iii) vmax of the photoelectrons
(b) Ultraviolet light of wavelength 280 nm is used in an experiment on photoelectric effict with lithium (ϕ=2.5eV) cathode. Find
(i) the maximum kinetic energy of the photoelectrons
(ii) the stopping potential
(c) Find the maximum magnitude of the linear momentum of a photelectron emitted when light of wavelength 400 nm falls on a metal (ϕ=2.5eV).
(d) A monochromitc light source of intensity 5 mW emits 8×105 photons per second. This light ejects photoelectrons from a metal surface. The stopping potential for this set up is 2.0V . Calculate the work function of the metal.
(e) The maximum kinetic energy of photoelectrons emitted from a certain metallic surface is 30 eV when imonochromatic radiation of wavelength λ falls on it. When the same surface is illuminated with light of wavelength 2λ the maximum kinetic energy of photo electrons is observed to be 10 eV. Calculate the wavelength λ and determine the maximum wavelength of incident radiation for which photoelectrons can be emitted by this surface.View Solution

