If f(x)=[cosx−sinx−sinxcosc1]andg(y)=[cosysinysinycosy], then [f(x)g(y)]−1 is equal to (a) f(−x)g(−y) (b) g(−y)f(−x) (c) f(x−1)g(y−1) (d) g(y−1)f(x−1)
Step by step video & image solution for If f(x)=[cosx-sinx -sin x cosc 1] and g(y)=[cosy sin y siny cos y], then [f(x)g(y)]^-1 is equal to (a) f(-x)g(-y) (b) g(-y)f(-x) (c) f(x^-1)g(y^-1) (d) g(y^-1)f(x^-1) by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
F(x)=⎡⎢⎣cosx−sinx0sinxcosx0001⎤⎥⎦ and G(x)=⎡⎢⎣cosx0sinx010−sinx0cosx⎤⎥⎦, then [F(x)G(y)]−1 is equal to (A) F(−x)G(−y) (B) F(x−1)G(y−1) (C) G(−y)F(−x) (D) G(y−1)F(x−1)
View SolutionLetf(x)=⎡⎢⎣cosx−sinx0sinxcosx0001⎤⎥⎦,then (A) (f(x))2=−I (B) f(x+y)=f(x),f(y) (C) f(x)−1=f(−x) (D) f(x)−1=f(x)
View Solution
Knowledge Check
If F(x)=⎡⎢⎣cosx−sinx0sinxcosx0001⎤⎥⎦ and G(y)=⎡⎢⎣cosy0siny010−siny0cosy⎤⎥⎦, then [F(x)G(y)]−1 is equal to
AF(−x)G(−y)BG(−y)F(−x)CF(x−1)G(y−1)DG(y−1)F(x−1)IfF(x)=⎡⎢⎣cosx−sinx0sinxcosx0001⎤⎥⎦,G(y)=⎡⎢⎣cosyosiny010−siny0cosy⎤⎥⎦,
then [f(x)⋅G(y)−1 is equal toAf(x)G(−y)BF−1(x)G−1(y)CG−1(y)F−1(x)DG(−y)F(−x)If f(x) = ⎡⎢⎣cosx−sinx0sinxcosx0001⎤⎥⎦ and g(y) = ⎡⎢⎣cosx0sinx010−sinx0cosx⎤⎥⎦ then [f(x)g(y)]−1 is equal to
Af(-x) g(-y)Bf(x−1)g(y−1)Cg(-y) f(-x)Dg(y−1)f(x−1)
If f(x) = ⎡⎢⎣cosx−sinx0sinxcosx0001⎤⎥⎦ then show f(x) . f(y) = f(x+y)
View SolutionGiven the graph of y=f(x).
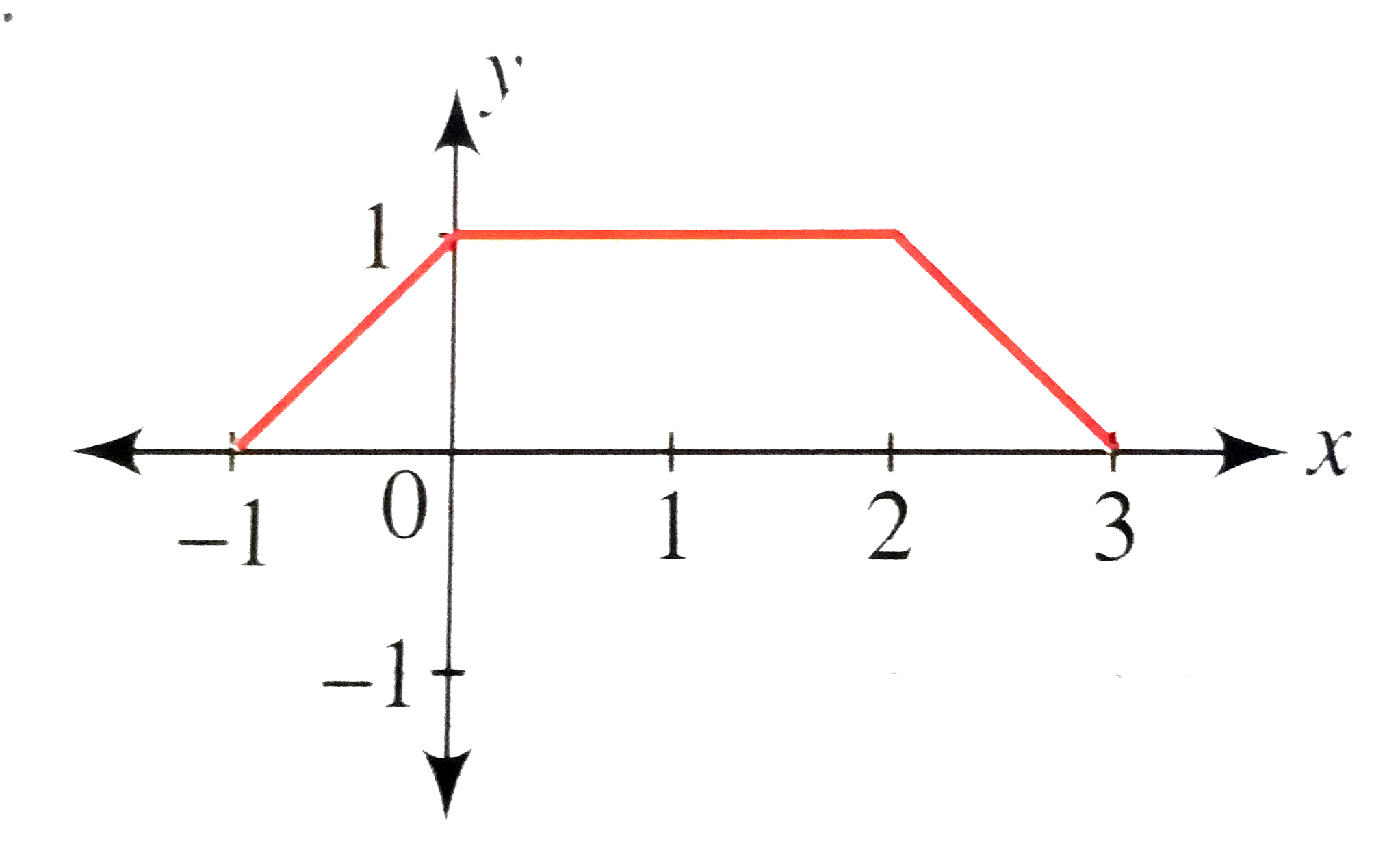
Draw the graphs of the followin.
(a) y=f(1−x) (b) y=−2f(x)
(c) y=f(2x) (d) y=1−f(x)
View SolutionIf f(x,y)=(max(x,y))min(x,y) and g(x,y)=max(x,y)−min(x,y), then f(g(−1,−32),g(−4,−1.75)) equals
View SolutionIf F(x)=⎡⎢⎣cosx−sinx0sinxcosx0001⎤⎥⎦ Show that F(x)F(y)=F(x+y)
View SolutionLet f(x+y)=f(x)f(y)andf(x)=1+(sin2x)g(x) where g(x) is continuous. Then, f'(x) equals
View Solution
