Two points charges q and -2q are placed some distance d apart. If the electric field at the location of q is E, that at the location of -2q is
−E2
−2E
E2
−4E
The correct Answer is:C
To solve the problem, we need to analyze the electric fields produced by the two point charges q and −2q at their respective locations.
1. Identify the Charges and Their Positions:
- We have two point charges: q (positive charge) and −2q (negative charge).
- They are placed a distance d apart.
2. Electric Field at Charge q:
- The electric field E at the location of charge q is due to the charge −2q.
- The electric field E created by a point charge is given by the formula:
E=k⋅|Q|r2
where k is Coulomb's constant, Q is the charge creating the field, and r is the distance from the charge to the point where the field is being calculated.
3. Calculate the Electric Field at Charge −2q:
- Now, we need to find the electric field at the location of charge −2q due to charge q.
- The distance from q to −2q is d.
- The electric field E′ at the location of −2q due to charge q is:
E′=k⋅|q|d2
4. Relate the Electric Fields:
- From the problem, we know that the electric field at the location of q is E.
- We can express E in terms of q and −2q:
E=k⋅|(−2q)|d2=2kqd2
- Now, we can relate E′ to E:
E′=k⋅|q|d2
- Notice that E′ is half of E:
E′=12⋅2kqd2=E2
5. Conclusion:
- The electric field at the location of charge −2q is:
E′=E2
Final Answer:
The electric field at the location of charge −2q is E2.
- We have two point charges: q (positive charge) and −2q (negative charge).
- They are placed a distance d apart.
- The electric field E at the location of charge q is due to the charge −2q.
- The electric field E created by a point charge is given by the formula:
E=k⋅|Q|r2
where k is Coulomb's constant, Q is the charge creating the field, and r is the distance from the charge to the point where the field is being calculated.
- Now, we need to find the electric field at the location of charge −2q due to charge q.
- The distance from q to −2q is d.
- The electric field E′ at the location of −2q due to charge q is:
E′=k⋅|q|d2
- From the problem, we know that the electric field at the location of q is E.
- We can express E in terms of q and −2q:
E=k⋅|(−2q)|d2=2kqd2
- Now, we can relate E′ to E:
E′=k⋅|q|d2
- Notice that E′ is half of E:
E′=12⋅2kqd2=E2
- The electric field at the location of charge −2q is:
E′=E2
The electric field at the location of charge −2q is E2.
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDSBook:NARAYNAChapter:ELECTRIC CHARGES AND FIELDSExercise:EXERCISE -1 (C.W)
Explore 24 Videos
- ELECTRIC CHARGES AND FIELDSBook:NARAYNAChapter:ELECTRIC CHARGES AND FIELDSExercise:EXERCISE -1 (H.W)
Explore 27 Videos
- ELECTRIC CHARGES AND FIELDSBook:NARAYNAChapter:ELECTRIC CHARGES AND FIELDSExercise:EVALUATE YOURSELF-4
Explore 6 Videos
- DUAL NATUREBook:NARAYNAChapter:DUAL NATUREExercise:LEVEL-II (H.W)
Explore 17 Videos
- ELECTRO MAGNETIC INDUCTIONBook:NARAYNAChapter:ELECTRO MAGNETIC INDUCTIONExercise:Level-II (H.W)
Explore 23 Videos
Similar Questions
Two point charges q and -q are separated by a distance 2a. Evaluate the flux of the electric field strength vector across a circle of radius R.

View SolutionTwo point charges q and −q are separated by the distance 2l. Find the flux of the electric field strength vector across a circle of radius R.

View Solution
Knowledge Check
Two point charges Q and −3Q are placed at some distance apart. If the electric field at the location of Q is E then at the locality of −3Q, it is
A−EBE/3C−3ED−E/3The point charges Q and −2Q are placed at some distance apart. If the electirc field at the location of Q is E, the electric field at the location of −2Q will be
A−3E2B−EC−E2D−2ETwo point charges q1andq2 are placed in an external uniform electric field as shown in figure. The potential at the location of q1andq2 are V1andV2, i.e., V1andV2 are potentials at location of q1andq2 due to external unspecified charges only. Then electric potential energy for this configuration of two charged particle is
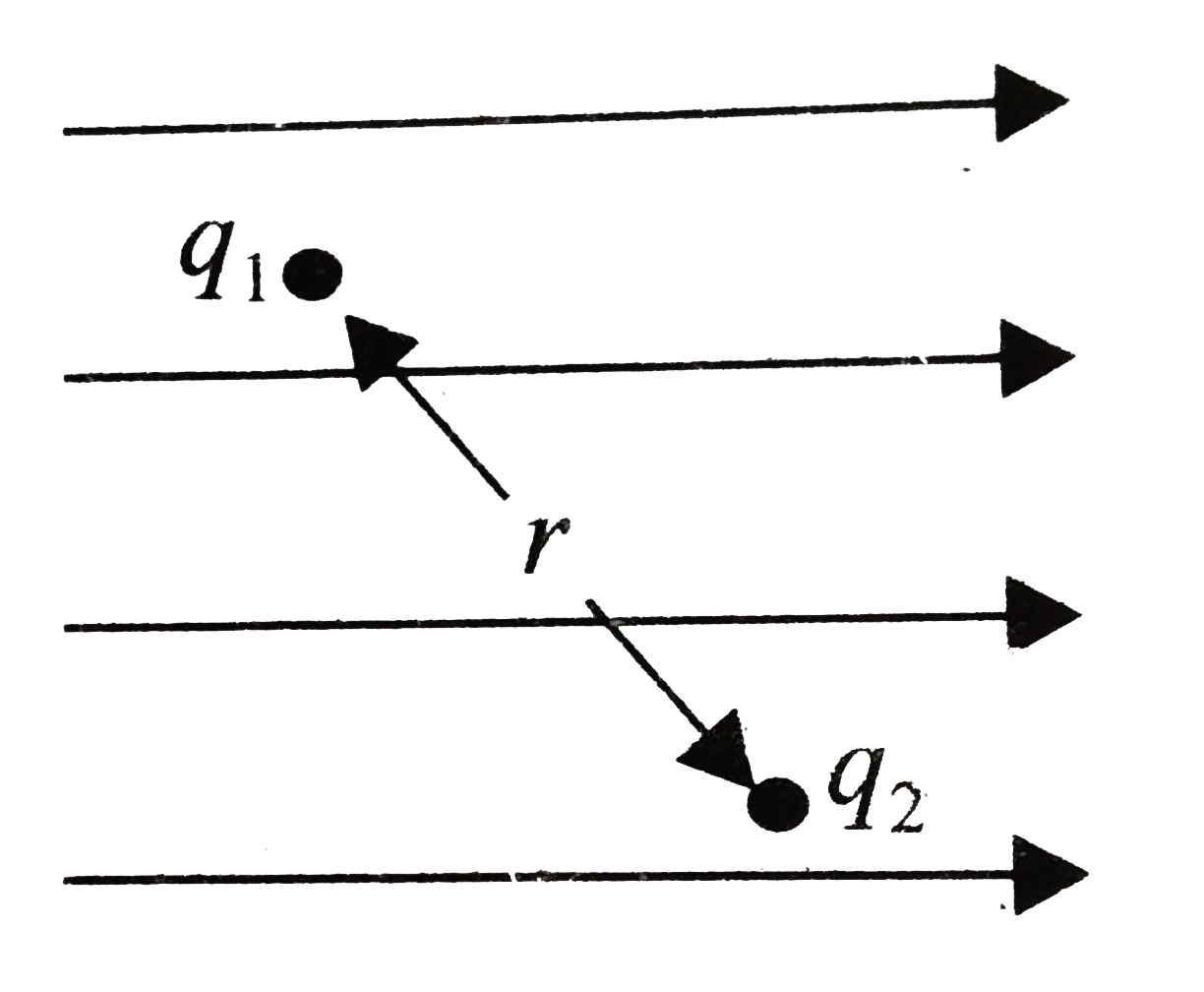 Aq1V1+q2V22Bq1V1+q2V2Cq1V1+q2V2+q1q24πε0rDq1q24πε0r
Aq1V1+q2V22Bq1V1+q2V2Cq1V1+q2V2+q1q24πε0rDq1q24πε0r
Two point charges+ q and-q are placed at distanced apart. What are the points at which the resultant field is parallel to the line joining the two charges ?
View SolutionTwo point charges q and −2q are kept 'd' distance apart. Find the location of the point relative to charge q at which potential due to the system of charges is zero.
View SolutionTwo charges 4q and q are placed 30 cm. apart. At what point the value of electric field will be zero
View SolutionTwo point charges 2q and 8q are placed at a distance r apart. Where should a third charge −q be placed between them so that the electrical potential energy of the system is a minimum
View SolutionTwo point charges +q and −q are placed a distance x apart. A third charge is so placed that al the three charges are in equilibrium. Then
View Solution