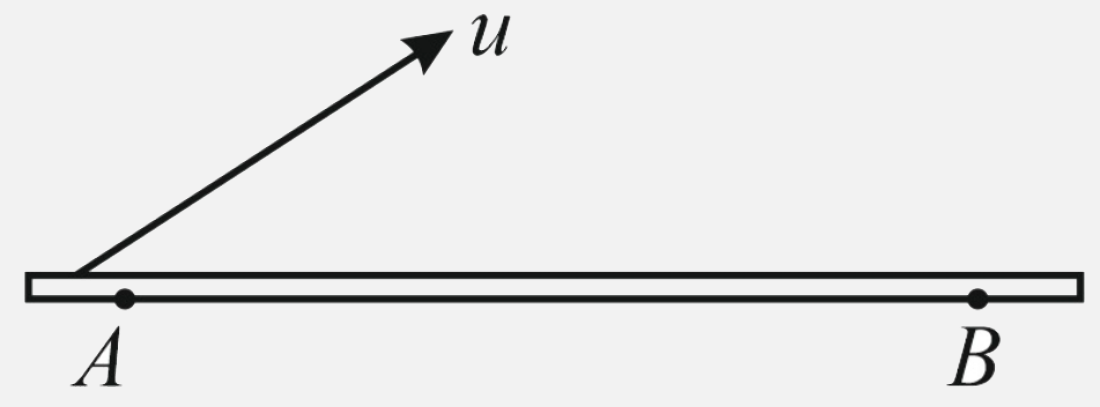
A large flat metal surface has a uniform charge density +σ. An electron of mass m and charge u and returns to it at point B. Disregard gravity . The maximum value of AB is
vmε0σe
v2mε0eσ
v2eε0σm
v2σeε0m
The correct Answer is:B
Field near metal surface E=σε0
Force on electron =eE=eσε0
Acceleration of electron a=eσmε0
It will act as projectile with max range
u2a=u2eσ×mε0
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDSBOOK - NARAYNACHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - EXERCISE -3
50 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - NARAYNACHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - EXERCISE -4
43 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - NARAYNACHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - EXERCISE -2 (C.W.)
39 Videos
- DUAL NATUREBOOK - NARAYNACHAPTER - DUAL NATUREEXERCISE - LEVEL-II (H.W)
17 Videos
- ELECTRO MAGNETIC INDUCTIONBOOK - NARAYNACHAPTER - ELECTRO MAGNETIC INDUCTIONEXERCISE - Level-II (H.W)
23 Videos
Similar Questions
A large flat metal surface has a uniform charge density (+σ). An electron of mass m and charge ρ leaves the surface at the point A with speed u and returns to it at point B. Disregarding gravity the maximum value of AB is
View SolutionTwo infinite, non-conducting sheets of charge are parallel to each other, as shown in figure. The sheet on the left has a uniform surface charge density σ, and the one on the right has a uniform charge density −σ. Calculate the electric field at points (a) to the left of, (b) in between, and (c) to the right of the two sheets.

View Solution
Knowledge Check
An infinite plane sheet of positive charge has surface charge density σ. A metallic ball of mass m and charge +Q is attached to a thred and is tied to a point A on the sheet PQ. The angle θ made by the string with plane sheet is in equilibrium is
AzeroBtan−1(Qσ4ε0mg)Ctan−1(Qσ2ε0mg)Dtan−1(Qσε0mg)A large nonconducting sheet M is given a uniform charge density. Two unchared small metal rods A and B are placed near the sheet as shown in figure
 AM attracts ABA attract BCM attracts BDB repels A
AM attracts ABA attract BCM attracts BDB repels AA sphere of radius R has a charge density σ. The electric intensity at a point at a distance r from its centre is
AE=σR2∈0kr2BE=σ∈0kCE=R2DE=∈0kr2σ2
(a) Use Gauss's theorem to find the electric field due to a uniformly charged infinitely
Iarge plane thin sheet with surface charge density.Σ
(b) An infinitely large thin plane sheet has a uniform surface charge density +σ. Obtain the
expression for the amount of work done in bringing a point charge q from infinity to a
point , distant r, in front of the charged plane sheet.
View SolutionA flat disc of radius R charged uniformly on its surface at a surface charge density σ. About its central axis of rotation it rotates at an angular speed ω. Find the magnetic moment of disc due to rotation of charges.
View SolutionA soap bubble (surface tension T) is charged to a uniform charged density σ. At equilibrium the radius of the bubble is given by Nε0Tσ2. The value of N is [Assume that atmosphere is not present]
View SolutionIn the figure shown S is a large nonconducting sheet of uniform charge density σ. A rod R of length l and mass 'm' is parallel to the sheet and hinged at its mid point. The linear charge densities on the upper and lower half of the rod are shown in the figure. Find the angular acceleration of the rod just after it is released.
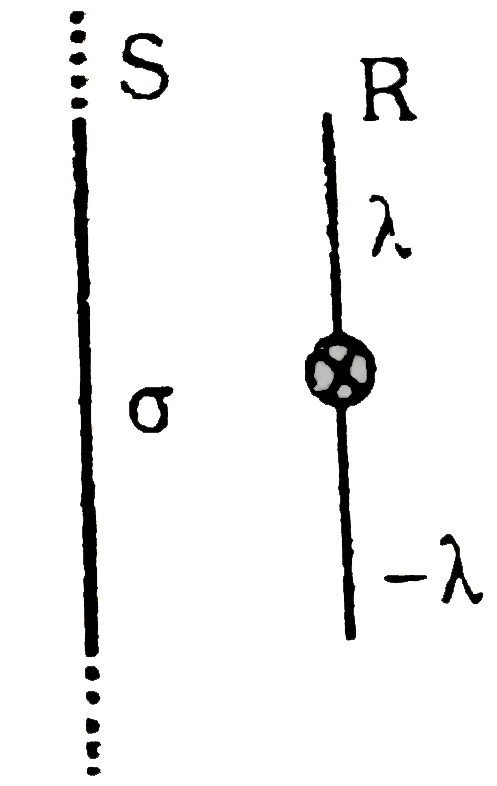
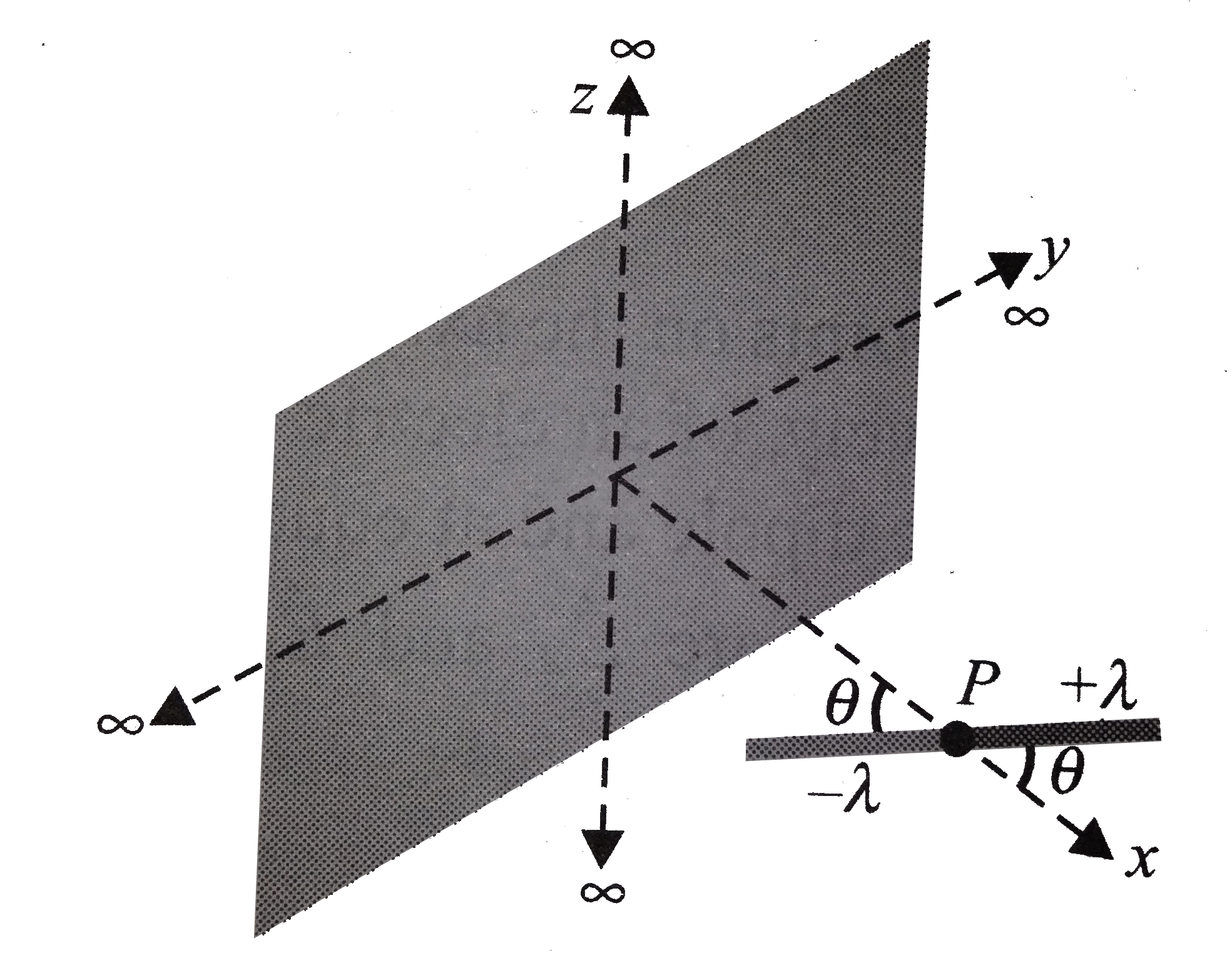
View SolutionA large sheet carries uniform surface charge density σ . A rod of length 2l has a linear charge density lamba on one half and −λ on the second half. The rod is hinged at the midpoint O and makes an angle θ with the normal to the sheet. The torque experience by the rod is
View Solution
