A charge +q0 is fixed at a position in space. From a large distance another charged particle of charge -q and mass m is thrown towards +q0 with an impact parameter L as shown. The initial speed of the projected particle is v. Find the distance of closer approach of the two particles?

As -q moves towards +q0 an attractive force acts on -q towards +q0 No torque acts on -q relative to +q0 because electrostatic force is a central force. In other words angular momentum of -q must remain constant. When -q is closest to +q0 it will be moving perpendicularly to the line joining the two charges as shwon −q

Let r be the closest separation between the charges and vc be the velocity of -q at that instant. From conservation of angular momentum, mvL = mvcr
From conservation of mechanical energy
12mv2=12mv2c−14π∈0qq0r
On solving the above equation, we can get r.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBOOK - NARAYNACHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - Evaluate yourself-1
5 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBOOK - NARAYNACHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - Evaluate yourself-2
8 Videos
- ELECTROMAGNETIC WAVES BOOK - NARAYNACHAPTER - ELECTROMAGNETIC WAVES EXERCISE - EXERCISE -4
15 Videos
- ELECTROSTATICS AND GAUSS LAWBOOK - NARAYNACHAPTER - ELECTROSTATICS AND GAUSS LAWEXERCISE - Intergers type question
11 Videos
Similar Questions
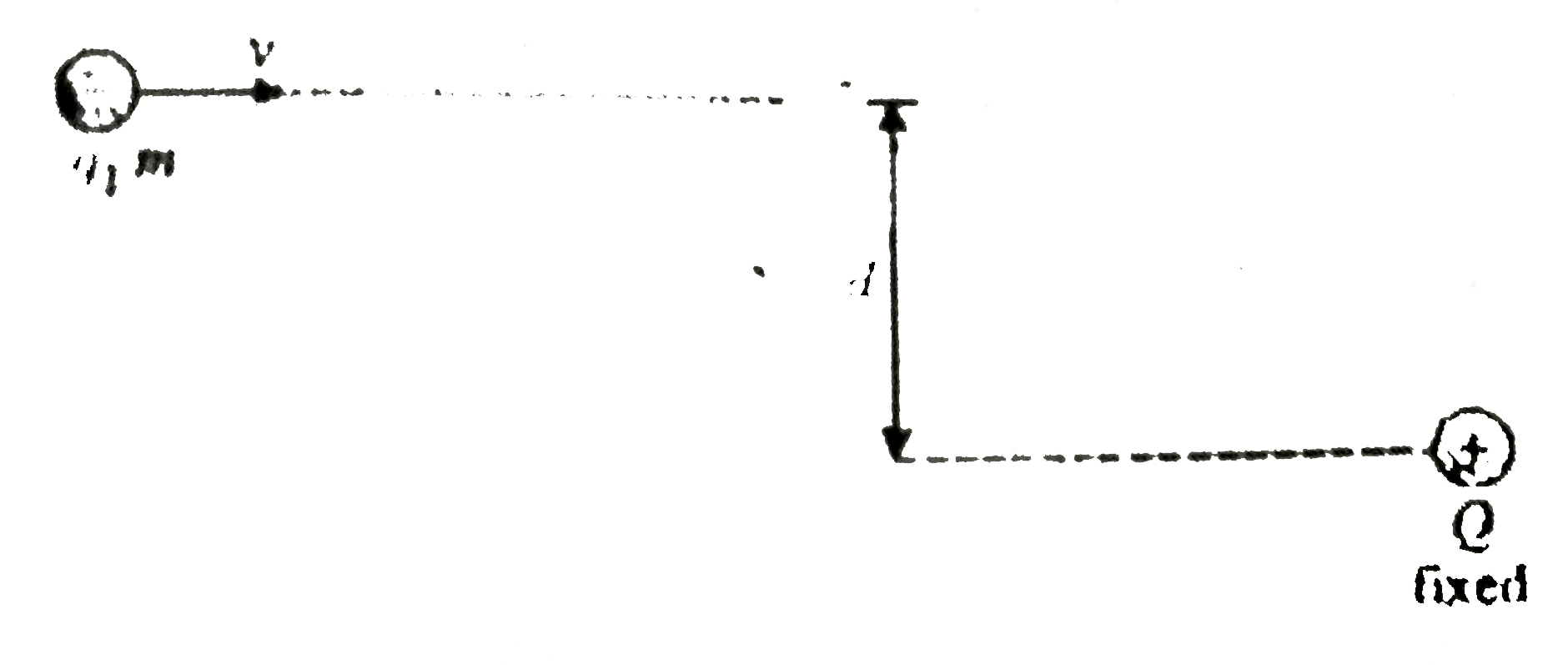
Figure shows a charge +Q clamped at a point in free space. From a large distance another charge particle of charge -q an.d mass m is thrown toward +Q with an impact parameter d as shown with speed v. Find the distance of closest approach of the two particles.
View SolutionA charge particle q1, is at position (2, -1, 3). The electrostatic force on another charged particle q2 at (0, 0, 0) is :
View Solution
Knowledge Check
A charge q of mass m is projected form a long distance with speed v towards another stationery particle of same mass and charge the distance of closet approach of the particles is
Aq22πε0mv2B2q2πε0mv2C3q22πε0mv2Dq2πε0mv2A charge particle q1, is at position (2, -1, 3). The electrostatic force on another charged particle q2 at (0, 0, 0) is :
Aq1q256π∈0(2ˆi−ˆj+3ˆk)Bq1q256√14π∈0(2ˆi−ˆj+3ˆk)Cq1q256π∈0(ˆj−2ˆi−3ˆk)Dq1q256√14π∈0(ˆj−2ˆi−3ˆk)
A long straight wire carries a current i. A particle having a positive charge q and mass m, kept at distance x0 from the wire is projected towards it with speed v. Find the closest distance of approach of charged particle to the wire.
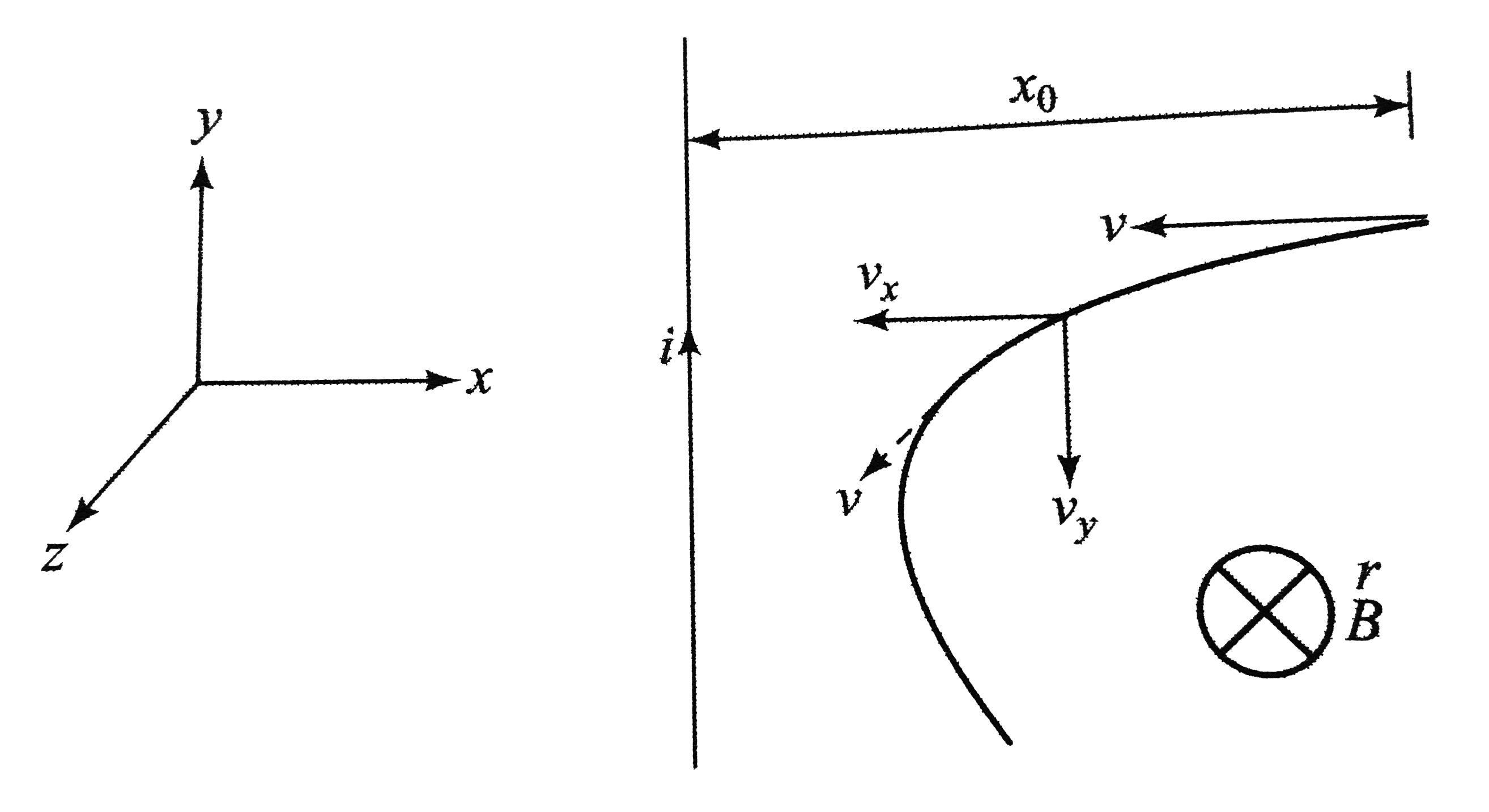

View SolutionA long straight wire carries a current i. A particle having a positive charge q and mass m, kept at distance x0 from the wire is projected towards it with speed v. Find the closest distance of approach of charged particle to the wire.


View SolutionA charged particle +q of mass m is placed at a distanced from another charged particle -2q of mass 2m in a uniform magnetic field B as shown in Fig. 1.28. If the particles are projected towards each other with same speed v,

a. find the maximum value of projected speed vm so that the two particles do not collide.
b. find the time after which collision occurs between the particles if projection speed equals 2vm.
c. Assuming the collision to be perfectly inelastic, find the radius of the particle in subsequent motion. (Neglect the electric force between the charges.)
View SolutionA particle of mass m and charge +q approaches from a very large distance towards a uniformly charged ring ofradius Rand charge, mass same as that of particle, with initial velocity v0 along the axis of the ring as shown in the figure-1.420. What is the closest distance of approach between the ring and the particle? Assume the space to be gravity free and frictionless :

View SolutionA particle of mass m and charge +q approaches from a very large distance towards a uniformly charged ring ofradius Rand charge, mass same as that of particle, with initial velocity v0 along the axis of the ring as shown in the figure-1.420. What is the closest distance of approach between the ring and the particle? Assume the space to be gravity free and frictionless :

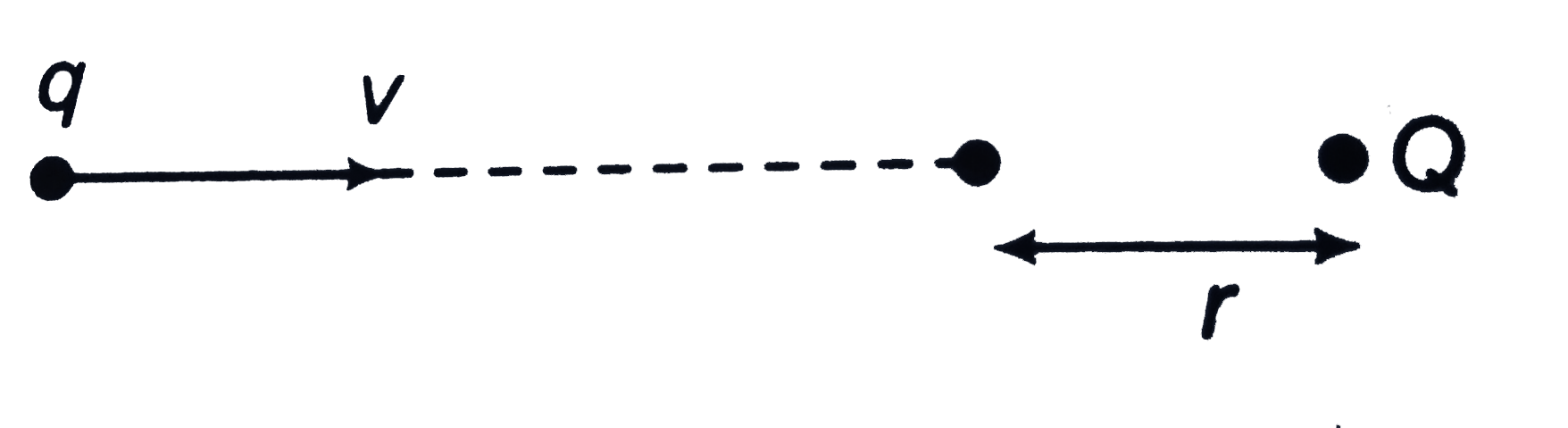
View SolutionA charged particle q is shot from a large distance towards another charged particle Q which is fixed, with speed v. It approaches Q up to as closed distance r and then returns. If q were given a speed 2v, the distasnce of approach would be
View Solution
