An oil drop 'B' has charge 1.6×10−19Cand mass 1.6×10−14kg. If the drop is in equilibrium position, then what will be potential difference between the plates. [The distance between the plates is 100mm]
To solve the problem of finding the potential difference between the plates given an oil drop in equilibrium, we can follow these steps:
1. Identify the Forces Acting on the Oil Drop:
The oil drop has a charge Q=1.6×10−19C and a mass m=1.6×10−14kg. When the drop is in equilibrium, the electric force acting on it due to the electric field between the plates balances the gravitational force acting on it.
2. Calculate the Gravitational Force:
The gravitational force Fg acting on the drop can be calculated using the formula:
Fg=m⋅g
where g is the acceleration due to gravity (approximately 10m/s2).
Fg=(1.6×10−14kg)⋅(10m/s2)=1.6×10−13N
3. Set Up the Electric Force Equation:
The electric force Fe acting on the oil drop is given by:
Fe=Q⋅E
where E is the electric field strength between the plates. In equilibrium, the electric force equals the gravitational force:
Q⋅E=m⋅g
4. Calculate the Electric Field:
Rearranging the equation gives:
E=m⋅gQ
Substituting the values we have:
E=(1.6×10−14kg)⋅(10m/s2)1.6×10−19C=1.6×10−131.6×10−19=106N/C
5. Calculate the Potential Difference:
The potential difference V between the plates can be calculated using the relation:
V=E⋅d
where d is the distance between the plates. Given d=100mm=0.1m:
V=(106N/C)⋅(0.1m)=105V
Final Answer:
The potential difference between the plates is 105V.
---
The oil drop has a charge Q=1.6×10−19C and a mass m=1.6×10−14kg. When the drop is in equilibrium, the electric force acting on it due to the electric field between the plates balances the gravitational force acting on it.
The gravitational force Fg acting on the drop can be calculated using the formula:
Fg=m⋅g
where g is the acceleration due to gravity (approximately 10m/s2).
Fg=(1.6×10−14kg)⋅(10m/s2)=1.6×10−13N
The electric force Fe acting on the oil drop is given by:
Fe=Q⋅E
where E is the electric field strength between the plates. In equilibrium, the electric force equals the gravitational force:
Q⋅E=m⋅g
Rearranging the equation gives:
E=m⋅gQ
Substituting the values we have:
E=(1.6×10−14kg)⋅(10m/s2)1.6×10−19C=1.6×10−131.6×10−19=106N/C
The potential difference V between the plates can be calculated using the relation:
V=E⋅d
where d is the distance between the plates. Given d=100mm=0.1m:
V=(106N/C)⋅(0.1m)=105V
The potential difference between the plates is 105V.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBOOK - NARAYNACHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - Evaluate yourself-1
5 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBOOK - NARAYNACHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - Evaluate yourself-2
8 Videos
- ELECTROMAGNETIC WAVES BOOK - NARAYNACHAPTER - ELECTROMAGNETIC WAVES EXERCISE - EXERCISE -4
15 Videos
- ELECTROSTATICS AND GAUSS LAWBOOK - NARAYNACHAPTER - ELECTROSTATICS AND GAUSS LAWEXERCISE - Intergers type question
11 Videos
Similar Questions
In Millikan's experiment, an oil drop of radius 10−4 cm remains suspended between the plates which are 1 cm apart. If the drop has charge of 5e over it, calculate the potential difference between the plates. The density of oil may be taken as 1.5gcm−3.
View SolutionA positively charged oil droplet remains in the electric field between two horizontal plates, separated by a distance 1cm. If the charge on the drop is 3:3×10−3C and the mass of the droplet is 1014kg, then what is the potential difference (in volt) between the plates? (Take g=9.9ms2 )
View Solution
Knowledge Check
A proton has a mass 1.67 ×10−27 kg and charge +1.6×10−19C. If the proton is accelerated through a potential difference of million volts, then the kinetic energy is
A1.6×10−15 JB1.6×10−13 JC1.6×10−21 JD3.2×10−13JA charged oil drop of mass 9.75×10−15kg and charge 30×10−16C is suspended in a uniform electric field existing between two parallel plates. The field between the plates is (take g=10ms−2)
A3.25Vm−1B300Vm−1C325Vm−1D32.5Vm−1The de-Broglie wavelength of proton ( charge=1.6×10−19C,mass=1.6×10−27Kg) accelerated through a potential difference of 1kV is
A600 ÅB0.9×10−12mC7 ÅD0.9 mm
In Millikan's oil drop experiment, a charged oil drop of mass 3.2×10−14kg is held stationary between two parallel plates 6mm apart by applying a potential difference of 1200V between them. How many excess electrons does the oil drop carry? Take g=10ms−2
View SolutionAn oil drop has 8.01×10−19C charg .Calculate the number of electrons in this drop.
View SolutionA particle of mass 9×10−31 kg having a negative charge of 1.6×10−19C is projected horizontally with a velocity of 106ms−1 into a region between two infinite horizontal parallel plates of metal. The distance between the plates is d=0.3cm and the particle enters 0.1cm below the top plate, THe top and bottom plates are connected, respectively to the positive and negative terminal of a 30V battery. Find the components of hte velocity of hte paricle just before it hits one of the plates.
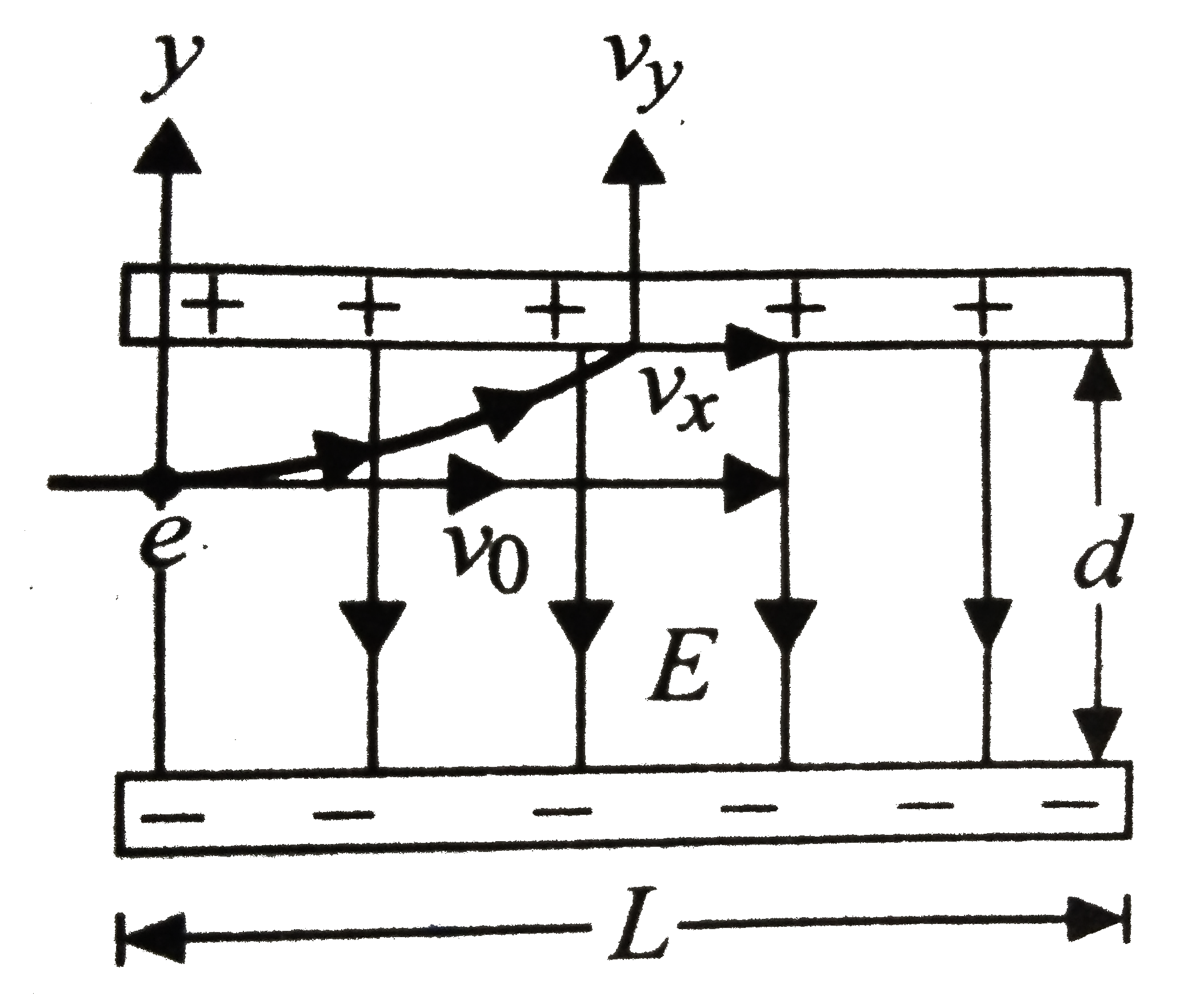
View SolutionA positively charged oil droplet remins stationary in the electric field between two horizontal plates separated by a distance of 1cm . The charge on the drop is 10−15C and mass of the droplet is 10−11g, the potential difference between the plates and if the polarity is reversed , the instantaneous of the droplet are
View SolutionIn Millikan oil drop experiment, a charged drop of mass 1.8×10−14kg is stationary between its plates. The distance between its plates is 0.90cm and potential difference is 2.0 kilo volts. The number of electrons on the drop is
View Solution
