Two circular loops of radii 0.05 and 0.09m, respectively , are put such that their axes coincide and their centre are 0.12 m apart. Charge of 10−6 coulomb is spread uniformly on each loop. Find the potential difference between the centres of loops.

The potential at the centre of a ring will be due to charge on both the rings and as every element of a ring is at a constant distance form the centre, so
V1=14πε0⎡⎢
⎢⎣q1R1+q2√R22+x2⎤⎥
⎥⎦
=9×109[10−45+10−4√92+122]
=9×105[15+115]=2.40×105V
similary , V2=14πε0⎡⎢
⎢⎣q2R2+q1√R21+x2⎤⎥
⎥⎦
or V2=9×103[19+113]=198117×105
V2=1.69×105V
So , V1−V2=(2.40−1.69)×105=71KV
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBOOK - NARAYNACHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - Evaluate yourself-1
5 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBOOK - NARAYNACHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - Evaluate yourself-2
8 Videos
- ELECTROMAGNETIC WAVES BOOK - NARAYNACHAPTER - ELECTROMAGNETIC WAVES EXERCISE - EXERCISE -4
15 Videos
- ELECTROSTATICS AND GAUSS LAWBOOK - NARAYNACHAPTER - ELECTROSTATICS AND GAUSS LAWEXERCISE - Intergers type question
11 Videos
Similar Questions
Two circular loops of radii 0.05 and 0.09m, respectively, are put such that their axes coincide and their centers are 0.12m apart. A charge of 10−6C is spread uniformly on each loop. Find the potential difference between the centers of the loops.
View SolutionRadii of two conducting circular loops are b and a respectively, where b>>a Centres of both loops coincide but planes of both loops are perpendicular each other. The value of mutual inductance for these loops
View Solution
Knowledge Check
Two circular loops of radii 0.05 and 0.09m, respectively, are put such that their axes coincide and their centers are 0.12m apart. A charge of 10−6C is spread uniformly on each loop. Find the potential difference between the centers of the loops.
A60KVB81KVC43KVD71KVA circular loop of radius 0.05 m carries a current of 1.0 A. The magnetic moment of the loop is .
A1.32×10−4A−m2B7.85×10−4A−m2C2.62×10−4A−m2D5.25×10−4A−m2A circular loop of radius 0.0157 m carriesa current of 2.0 A. The magnetic field at the centre of the loop is
A1.57×10−5Wb/m2B8.0×10−6Wb/m2C2.5×10−5Wb/m2D3.14×10−5Wb/m2
A circular loop of one turn carries a current of 5.00 A. If the magnetic field B at the centre is 0.200 mT, find the radius of the loop.
View SolutionA circular loop of radius0.05 m carriess a current of 1.0 A. The magnetic moment of the loop is .
View SolutionTwo coaxial circular loops of radius 0.5m and 5×10−2m are separated by a distance 0.5m and carry currents 2A and 1A respectively. The force between the loops due to mutual induction is
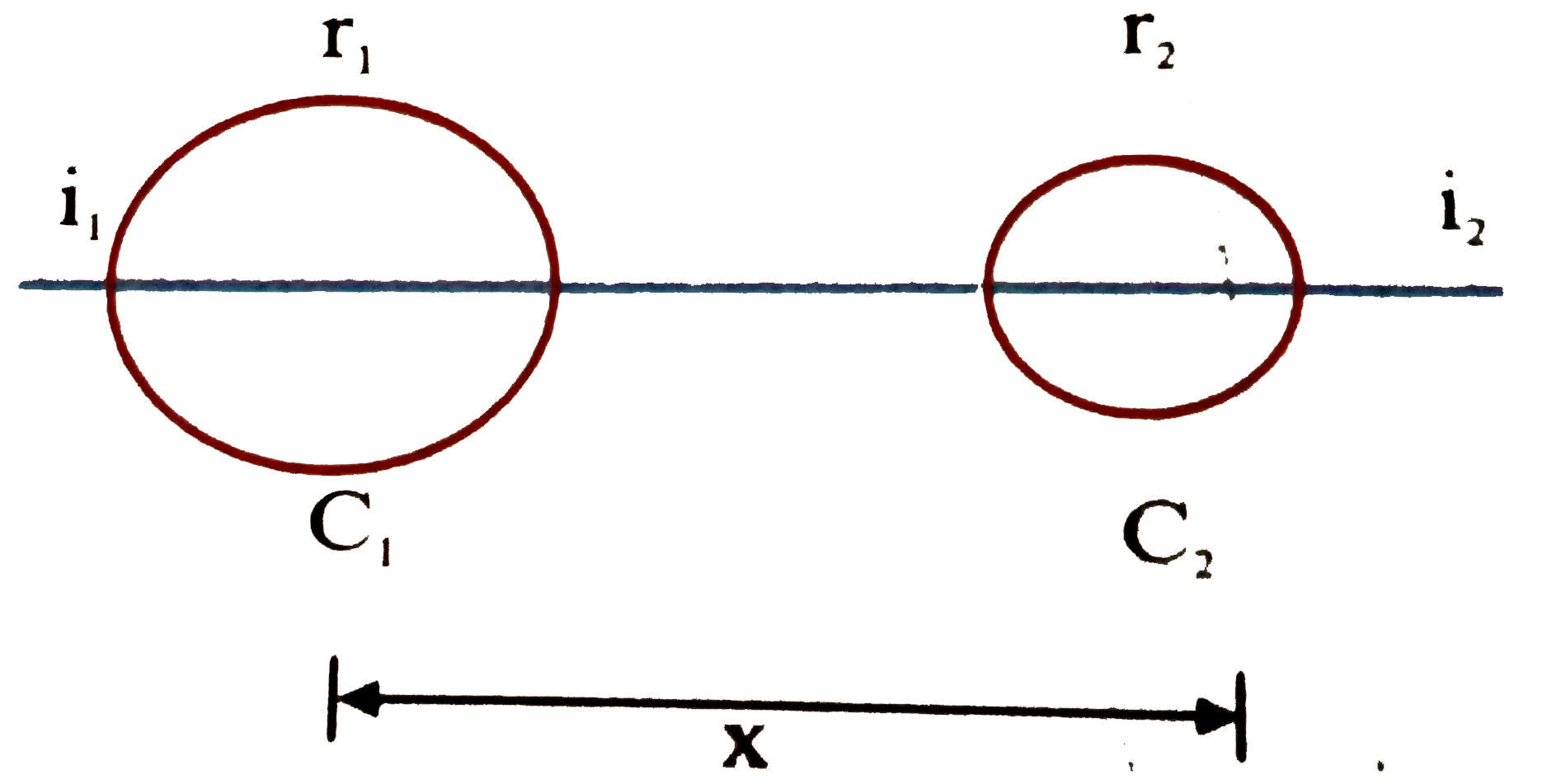
View SolutionRadii of two conducting circular loops are b and a respectively, where b>>a Centres of both loops coincide but planes of both loops are perpendicular each other. The value of mutual inductance for these loops
View SolutionA circular loop of radius 0.0157m carries a current of 2.0 amp. The magnetic field at the centre of the loop is
(μ0=4π×10−7weber/amp−m)
View Solution
