Two capacitors of capacitance 20.0 pF and 50.0 pF are connected is series with a battery of 20 V. Find the energy supplied by the battery.
To find the energy supplied by the battery when two capacitors are connected in series, we can follow these steps:
Step 1: Identify the capacitances
The given capacitances are:
- C1=20.0pF=20×10−12F
- C2=50.0pF=50×10−12F
Step 2: Calculate the equivalent capacitance for capacitors in series
For capacitors in series, the equivalent capacitance Ceq can be calculated using the formula:
1Ceq=1C1+1C2
Substituting the values:
1Ceq=120×10−12+150×10−12
Calculating the individual terms:
1Ceq=120×10−12+150×10−12=5100×10−12+2100×10−12=7100×10−12
Thus,
Ceq=100×10−127≈14.29×10−12F≈14.3pF
Step 3: Calculate the charge supplied by the battery
The charge Q supplied by the battery can be calculated using the formula:
Q=Ceq×V
where V=20V.
Substituting the values:
Q=14.3×10−12F×20V=286×10−12C=2.86×10−10C
Step 4: Calculate the energy supplied by the battery
The energy U supplied by the battery can be calculated using the formula:
U=Q×V
Substituting the values:
U=2.86×10−10C×20V=5.72×10−9J
Final Answer
The energy supplied by the battery is approximately:
U≈5.72nJ
The given capacitances are:
- C1=20.0pF=20×10−12F
- C2=50.0pF=50×10−12F
For capacitors in series, the equivalent capacitance Ceq can be calculated using the formula:
1Ceq=1C1+1C2
1Ceq=120×10−12+150×10−12
1Ceq=120×10−12+150×10−12=5100×10−12+2100×10−12=7100×10−12
Ceq=100×10−127≈14.29×10−12F≈14.3pF
The charge Q supplied by the battery can be calculated using the formula:
Q=Ceq×V
where V=20V.
Q=14.3×10−12F×20V=286×10−12C=2.86×10−10C
The energy U supplied by the battery can be calculated using the formula:
U=Q×V
U=2.86×10−10C×20V=5.72×10−9J
The energy supplied by the battery is approximately:
U≈5.72nJ
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - Evaluate yourself-15videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - NARAYNACHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - Evaluate yourself-28videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - NARAYNACHAPTER - ELECTROMAGNETIC WAVES EXERCISE - EXERCISE -415videos
ELECTROMAGNETIC WAVES
- BOOK - NARAYNACHAPTER - ELECTROSTATICS AND GAUSS LAWEXERCISE - Intergers type question11videos
ELECTROSTATICS AND GAUSS LAW
Similar Questions
Knowledge Check
- Question 1 - Select One
Two capacitors of capacities 1μF and 4μF are connected in series with battery of 200V. The voltage across them are in the ratio of
A12B21C14D41 - Question 2 - Select One
A capacitor of capacitance 10μF is charged by connecting through a resistance of 20Omga and battery of 20 V. What is the energy supplied by the battery?
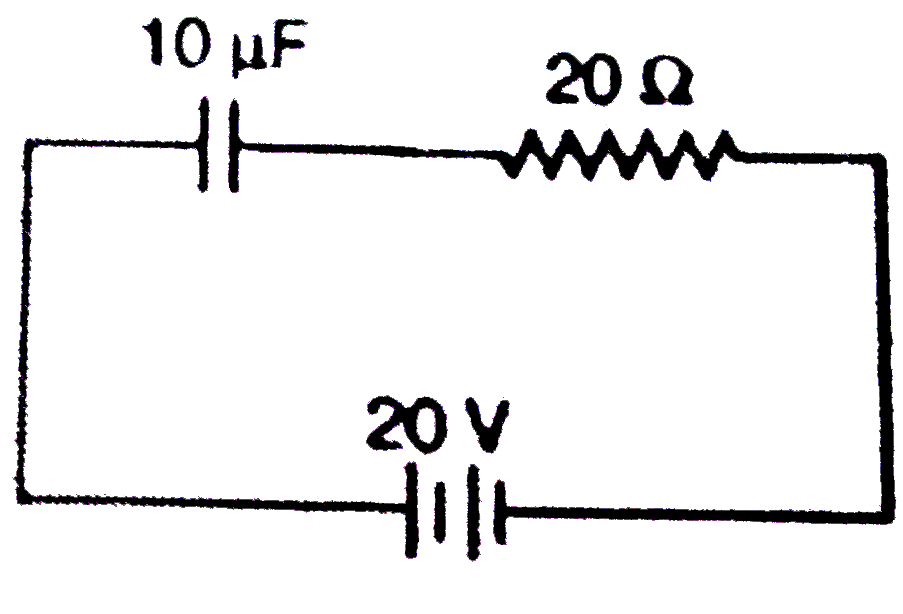 ALess than 2 mJBEqual to 2 mJCMore than 2 mJDCannot be predicted
ALess than 2 mJBEqual to 2 mJCMore than 2 mJDCannot be predicted
Two capacitors of capacitances 20.0pF and 50.0pF are connected in series with a 6.00V bettery . Find (a )the potential difference across each capacitor and (b) the energy stored in each capacitor .
View SolutionTwo capacitors of capacitance 10μFand20μF are connected in series with a 6 V battery. If E is the energy stored in 20μF capacitor what will be the total energy supplied by the battery in terms of E.
View SolutionTwo capacitors of capacitances 25μFand100μF are connected in series and are charged by a battery of 120 V. the battery is then removed. The capacitors are now separated and connected in paralle. Fiond (i) p.d. across each capacitor (ii) energy-loss in the process.
View SolutionP and Q are two capacitors with capacitance 10μF and 20μF respectively which are connected in series with a battery of value 12V. Find the ratio between the charges and P and Q.
View SolutionTwo capacitors of capacitance of 6μFand12μF are connected in series with a battery. The voltage across the 6μF capacitor is 2V. Compute the total battery voltage.
View SolutionTwo capacitors of capacitance of 6μFand12μF are connected in series with a battery. The voltage across the 6μF capacitor is 2 V.Compute the total battery voltage.
View Solution

