Question

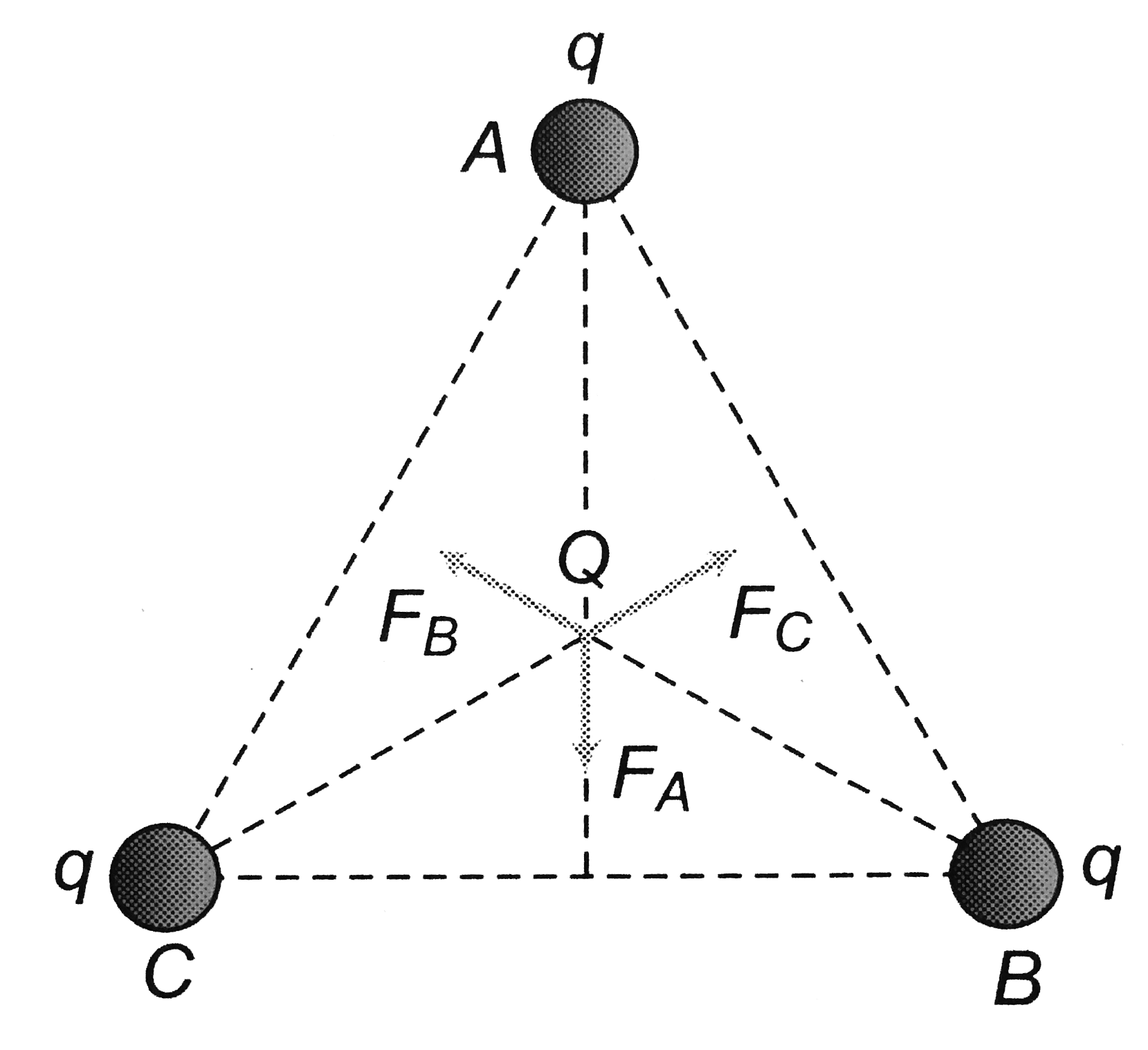
At each corner of an equilateral triangle identical charges are placed. Then at the centre of the triangle

Options

A. the resultant electric intensity is zero
B. the net potential is zero
C. both electric intensity and potential are zero
D. neither electric intensity nor potential are zero

Answer

A

Explanation

To solve the problem of identical charges placed at each corner of an equilateral triangle and to analyze the electric field and potential at the center of the triangle, we can follow these steps:

1. Understanding the Configuration:
- We have an equilateral triangle with identical charges \( Q \) placed at each of the three corners (let's label them as \( A \), \( B \), and \( C \)).
- The center of the triangle, known as the centroid, is the point where the medians of the triangle intersect.

2. Identifying the Centroid:
- For an equilateral triangle, the centroid divides each median in a 2:1 ratio. The centroid is equidistant from all three vertices.

3. Calculating the Electric Field at the Centroid:
- The electric field \( \vec{E} \) due to a point charge \( Q \) at a distance \( r \) is given by:
\( \vec{E} = \frac{1}{4\pi \epsilon_0} \frac{Q}{r^2} \)
- At the centroid, the contributions to the electric field from each charge will have both magnitude and direction.

4. Direction of Electric Field:
- The electric field due to each charge \( Q \) will point away from the charge (since they are positive charges).
- The angles between the lines connecting the centroid to each charge will be \( 120^\circ \) because of the symmetry of the equilateral triangle.

5. Resultant Electric Field:
- When we resolve the electric fields into components, the horizontal components (x-components) from each charge will cancel out due to symmetry.
- The vertical components (y-components) will also cancel out because they are equal in magnitude but opposite in direction.
- Therefore, the net electric field \( \vec{E}_{net} \) at the centroid is:
\( \vec{E}_{net} = 0 \)

6. Calculating the Electric Potential at the Centroid:
- The electric potential \( V \) due to a point charge \( Q \) at a distance \( r \) is given by:
\( V = \frac{1}{4\pi \epsilon_0} \frac{Q}{r} \)
- Since potential is a scalar quantity, the potentials from each charge at the centroid will simply add up.
- The total potential \( V_{total} \) at the centroid due to the three charges is:
\( V_{total} = V_A + V_B + V_C = 3 \times \frac{1}{4\pi \epsilon_0} \frac{Q}{r} \)
- Here, \( r \) is the distance from the centroid to any vertex.

7. Conclusion:
- The electric field at the center of the triangle is zero.
- The electric potential at the center of the triangle is non-zero and equal to \( \frac{3Q}{4\pi \epsilon_0 r} \).

Final Answer:
- Electric Field at the center: Zero
- Electric Potential at the center: Non-zero