An electron having charge e located at A, in the presence of a point charge +q located at O, is moved to the point B such that OAB forms an equilateral triangle the work done in the process is equal to
qAB
eqAB
−eq(AB)
zero
The correct Answer is:D
To solve the problem, we need to calculate the work done when an electron is moved from point A to point B in the electric field created by a point charge +q located at point O. The points A, B, and O form an equilateral triangle.
1. Understanding the Setup:
- We have a point charge +q at point O.
- An electron (which has a charge of -e) is initially at point A.
- The electron is moved to point B such that OAB forms an equilateral triangle.
2. Identifying the Potential:
- The electric potential V due to a point charge q at a distance r is given by the formula:
V=kqr
where k is Coulomb's constant.
3. Distance Between Points:
- Since OAB forms an equilateral triangle, the distance OA (from O to A) and OB (from O to B) are equal. Let's denote this distance as r.
4. Calculating the Potential at Points A and B:
- The potential at point A due to charge +q is:
VA=kqr
- The potential at point B due to charge +q is also:
VB=kqr
5. Finding the Potential Difference:
- The potential difference VB−VA is:
VB−VA=kqr−kqr=0
6. Calculating the Work Done:
- The work done W in moving a charge Q through a potential difference V is given by:
W=Q⋅(VB−VA)
- Here, Q is the charge of the electron, which is -e:
W=−e⋅0=0
Conclusion:
The work done in moving the electron from point A to point B is 0.
---
- We have a point charge +q at point O.
- An electron (which has a charge of -e) is initially at point A.
- The electron is moved to point B such that OAB forms an equilateral triangle.
- The electric potential V due to a point charge q at a distance r is given by the formula:
V=kqr
where k is Coulomb's constant.
- Since OAB forms an equilateral triangle, the distance OA (from O to A) and OB (from O to B) are equal. Let's denote this distance as r.
- The potential at point A due to charge +q is:
VA=kqr
- The potential at point B due to charge +q is also:
VB=kqr
- The potential difference VB−VA is:
VB−VA=kqr−kqr=0
- The work done W in moving a charge Q through a potential difference V is given by:
W=Q⋅(VB−VA)
- Here, Q is the charge of the electron, which is -e:
W=−e⋅0=0
The work done in moving the electron from point A to point B is 0.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBOOK - NARAYNACHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - EXERCISE - 3 (PREVIOUS AIPMT QUESTIONS)
23 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBOOK - NARAYNACHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - EXERCISE - 4 (NCERT EXAMPLAR PROBLEMS)
6 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBOOK - NARAYNACHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - Exercise-2(C.W)
53 Videos
- ELECTROMAGNETIC WAVES BOOK - NARAYNACHAPTER - ELECTROMAGNETIC WAVES EXERCISE - EXERCISE -4
15 Videos
- ELECTROSTATICS AND GAUSS LAWBOOK - NARAYNACHAPTER - ELECTROSTATICS AND GAUSS LAWEXERCISE - Intergers type question
11 Videos
Similar Questions
A charge (-q)and anther charge (+Q) are kept at two point A and B respectively, keeping the charge (+Q) fixed at B, the charge (-q)at A is moved to another points C,such that ABC forms an equilateral triangle of side l. The net work done in moving the charge(-q) is
View SolutionA charge q is moved from a point A above a dipole moment p to a point B below the dipole on equatorial plane without acceleration. Find the work done in the process.

View Solution
Knowledge Check
A charge (−q) and another charge (Q) are kept at two points AandB respectively. Keeping the charge (+Q) fixed at B, the charge (−q) at A is moved to another point C such that ABC forms an equilateral triangle of side l. The net work done in moving teh charge (−q) is
A14πε0QqlB14πε0Qql2C14πε0QqlDZeroA positive point charge q is carried from a point B to a point A in the electric field of a point charge +Q at O. If the permittivity of free space is ε0, the work done in the process is given by (where a=OA and b=OB) -
AqQ4πε0(1a+1b)BqQ4πε0(1a−1b)CqQ4πε0(1a2−1b2)DqQ4πε0(1a2+1b2)Three charges 2q,−q,and−q are located at the vertices of an equilateral triangle. At the center of the triangle,
Athe field is zero but potential is nonzero.Bthe field is nonzero but potential is zero.Cboth field and potential are zero.Dboth field and potential are nonzero.
A charge q0 is moved from a point A above a dipole of dipole moment p to a point B below the dipole at equatorial plane without acceleration. Find the work done in the process.
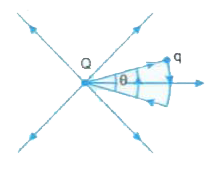
View SolutionA test charge q is made to move in the electric field of a point charge +Q along a closed path as shown in figure. What is the work done ?
View SolutionO is a point in the interior of a square ABCD such that ΔOAB is an equilateral triangle . Show that ΔOCD is an isoceles triangle .
View SolutionA charge is taken from a point A to a point B. The work done per unit charge in the process is called
View SolutionIn the electric field of a point chargde q, a cetrain charge is carried from point A to B,C,D and E. Then the ork done

View Solution
