A parallel plate capacitor has the space between its plates filled by two slabs of thickness d2 each and dielectric constant K1 and K2. d is the plate separation of the capacitor. The capacitance of the capacitor is
2ε0Ad(K1+K2K1K2)
2ε0Ad(K1+K2)
2ε0Ad(K1K2K1+K2)
`(2epsilon_(0)d)/(A) ((K_(1)+K_(2))/(K_(1)K_(2)))`
The correct Answer is:C
To solve the problem of finding the capacitance of a parallel plate capacitor with two dielectric slabs, we can follow these steps:
1. Identify the Configuration:
We have a parallel plate capacitor with plate separation d. The space between the plates is filled with two dielectric slabs, each of thickness d2 and dielectric constants K1 and K2.
2. Capacitance of Each Dielectric Section:
The capacitance C of a parallel plate capacitor filled with a dielectric is given by:
C=Kϵ0Ad
where K is the dielectric constant, ϵ0 is the permittivity of free space, A is the area of the plates, and d is the separation between the plates.
3. Calculate Capacitance for Each Section:
- For the first dielectric slab with dielectric constant K1 and thickness d2:
C1=K1ϵ0Ad2=2K1ϵ0Ad
- For the second dielectric slab with dielectric constant K2 and thickness d2:
C2=K2ϵ0Ad2=2K2ϵ0Ad
4. Determine the Connection Type:
Since the two dielectrics are arranged in series, we need to find the equivalent capacitance Ceq of the two capacitors C1 and C2.
5. Use the Formula for Series Capacitance:
The formula for the equivalent capacitance of capacitors in series is:
1Ceq=1C1+1C2
6. Substitute C1 and C2:
1Ceq=12K1ϵ0Ad+12K2ϵ0Ad
This simplifies to:
1Ceq=d2K1ϵ0A+d2K2ϵ0A
1Ceq=d2ϵ0A(1K1+1K2)
7. Combine the Terms:
1Ceq=d2ϵ0A⋅K1+K2K1K2
8. Invert to Find Ceq:
Ceq=2ϵ0AK1K2d(K1+K2)
Final Result:
The capacitance of the capacitor is:
Ceq=2K1K2ϵ0Ad(K1+K2)
We have a parallel plate capacitor with plate separation d. The space between the plates is filled with two dielectric slabs, each of thickness d2 and dielectric constants K1 and K2.
The capacitance C of a parallel plate capacitor filled with a dielectric is given by:
C=Kϵ0Ad
where K is the dielectric constant, ϵ0 is the permittivity of free space, A is the area of the plates, and d is the separation between the plates.
- For the first dielectric slab with dielectric constant K1 and thickness d2:
C1=K1ϵ0Ad2=2K1ϵ0Ad
- For the second dielectric slab with dielectric constant K2 and thickness d2:
C2=K2ϵ0Ad2=2K2ϵ0Ad
Since the two dielectrics are arranged in series, we need to find the equivalent capacitance Ceq of the two capacitors C1 and C2.
The formula for the equivalent capacitance of capacitors in series is:
1Ceq=1C1+1C2
1Ceq=12K1ϵ0Ad+12K2ϵ0Ad
This simplifies to:
1Ceq=d2K1ϵ0A+d2K2ϵ0A
1Ceq=d2ϵ0A(1K1+1K2)
1Ceq=d2ϵ0A⋅K1+K2K1K2
Ceq=2ϵ0AK1K2d(K1+K2)
The capacitance of the capacitor is:
Ceq=2K1K2ϵ0Ad(K1+K2)
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBOOK - NARAYNACHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - EXERCISE - 3 (PREVIOUS AIPMT QUESTIONS)
23 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBOOK - NARAYNACHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - EXERCISE - 4 (NCERT EXAMPLAR PROBLEMS)
6 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBOOK - NARAYNACHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - Exercise-2(C.W)
53 Videos
- ELECTROMAGNETIC WAVES BOOK - NARAYNACHAPTER - ELECTROMAGNETIC WAVES EXERCISE - EXERCISE -4
15 Videos
- ELECTROSTATICS AND GAUSS LAWBOOK - NARAYNACHAPTER - ELECTROSTATICS AND GAUSS LAWEXERCISE - Intergers type question
11 Videos
Similar Questions
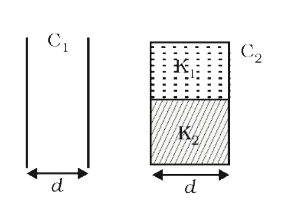
You are given an air filled parallel plate capacitor c1. The space between its plates is now filled with slabs of dielectric constant k1andk2 as shown in c2. Find the capacitances of the capacitor c2 if area of the plates is A distance between the plates is d.
View SolutionThe capacitance of a parallel plate capacitor with plate area A and separation d is C. The space between the plates in filled with two wedges of dielectric constants K1 and K2 respectively. Find the capacitance of resulting capacitor.

View Solution
Knowledge Check
A parallel plate capacitor has plate area A and plate separation d. The space between the plates is filled up to a thickness x<d with a dielectric constant K. Calculate the capacitance of the system.
 A2KεAKd−x(K−1)BKεAK2d−x(K−1)CKεAK−x(K−1)DKεAKd−x(K−1)
A2KεAKd−x(K−1)BKεAK2d−x(K−1)CKεAK−x(K−1)DKεAKd−x(K−1)A parallel plate capacitor of plate area A and separation d is filled with two materials each of thickness d2 and dielectric constants ∈1 and ∈2 respectively. The equivalent capacitance will be
 A∈0Ad(∈1+∈2)B∈0Ad(∈1+∈2)∈1∈2C2∈0Ad∈1∈2(∈1+∈2)D2∈0Ad(∈1+∈2)∈1∈2
A∈0Ad(∈1+∈2)B∈0Ad(∈1+∈2)∈1∈2C2∈0Ad∈1∈2(∈1+∈2)D2∈0Ad(∈1+∈2)∈1∈2A parallel plate capacitor with air between the plates has capacitance of 9pF. The separation between its plates is 'd'. The space between the plates is now filled with two dielectrics. One of the dielectrics has dielectric constant k1=3 and thickness d3 while the other one has dielectric constant k2=6 and thickness 2d3. Capacitance of the capacitor is now
A1.8 pFB45 pFC40.5 pFD20.25pF
The capacitance of a parallel plate capacitor with plate area A and separation d is C. The space between the plates in filled with two wedges of dielectric constants K1 and K2 respectively. Find the capacitance of resulting capacitor.

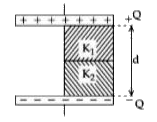
View SolutionA parallel-plate capacitor with plate area A has separation d between the plates. Two dielectric slabs of dielectric constant K1 and K2 of same area A/2 and thickness d/2 are inserted in the space between the plates. The capacitance of the capacitor will be given by :
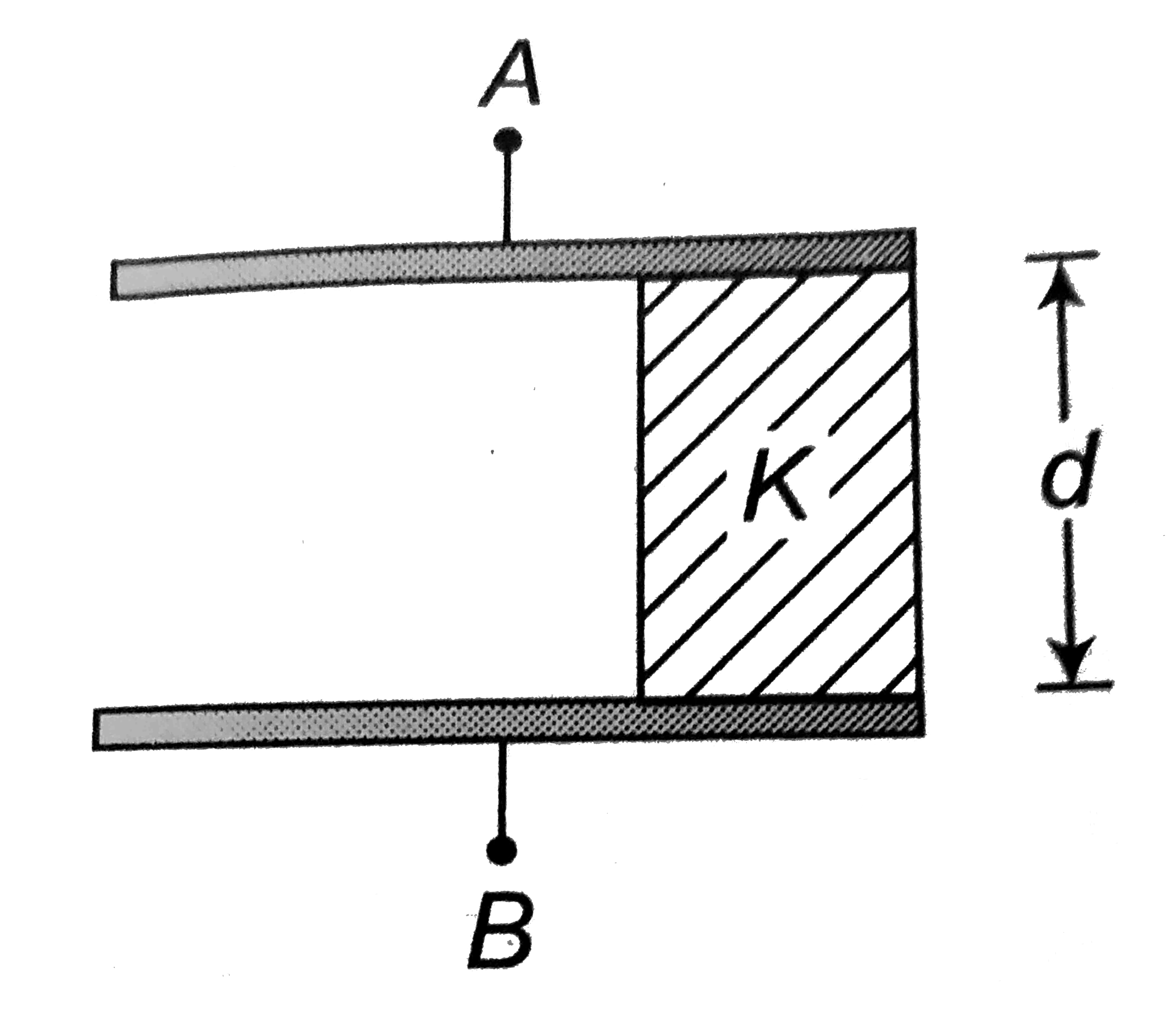
View SolutionA parallel plate capacitor with vacuum between its plates has capacitance C. A slabe of dielectric constant K and having the same thickness as the separation between the plates is introduced so as to fill 1/3rd of the capacitor as shown in the figure. the new capacitance will be
View SolutionIf a dielectric slab of thickness 5 mm and dielectric constant K=6 is introduced between the plates of a parallel plate air capacitor, with plate separation of 8 mm, then its capacitance is
View SolutionA parallel plate capacitor with oil as a dielectric between the plates has a capacitance C. if the oil, with dielectric constannt (K=3), is removed, then the capacitance of the capacitor will be
View Solution
