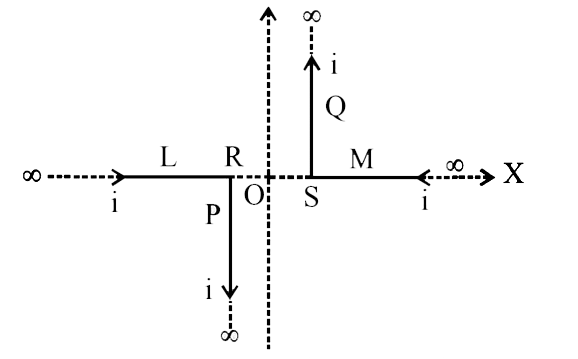
A pair of stationary and infinitely long bent wires is placed in the X−Y plane as shown in figure.The wires carry currents of 10A each as shown.The segments L and M are along the x-axis.The segments P and Q are pallel to the Y-axis such that OS=OR=0.02m.Find the magnitude and direction of the magnetic induction at the origin O.

Since point O is along the length of segment L and M the field at O due to these two segments will be zero
∴ Magnetic field at O is due to QS and RP.
∴BSQ=μ0I4π×IOS=10−7×100.02⊙
BRP=μ04π×IOR=10−7×100.02⊙
∴Bo=BSQ+BRP=10−7×100.02×2=10−4T⊙
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBOOK - NARAYNACHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - C.U.Q (AMPERE.S CIRCUITAL LAW MAGNETIC FIELD DUE TO STRAIGHT CONDUCTOR )
28 Videos
- MOVING CHARGES AND MAGNETISMBOOK - NARAYNACHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - C.U.Q (TANGENT GALVANOMETER)
8 Videos
- MOVING CHARGES AND MAGNETISMBOOK - NARAYNACHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Level -II (H.W)
37 Videos
- MAGNETISM AND MATTERBOOK - NARAYNACHAPTER - MAGNETISM AND MATTEREXERCISE - EXERCISE - 4 (SINGLE ANSWER TYPE QUESTION)
17 Videos
- NUCLEAR PHYSICSBOOK - NARAYNACHAPTER - NUCLEAR PHYSICSEXERCISE - LEVEL-II-(H.W)
9 Videos
Similar Questions
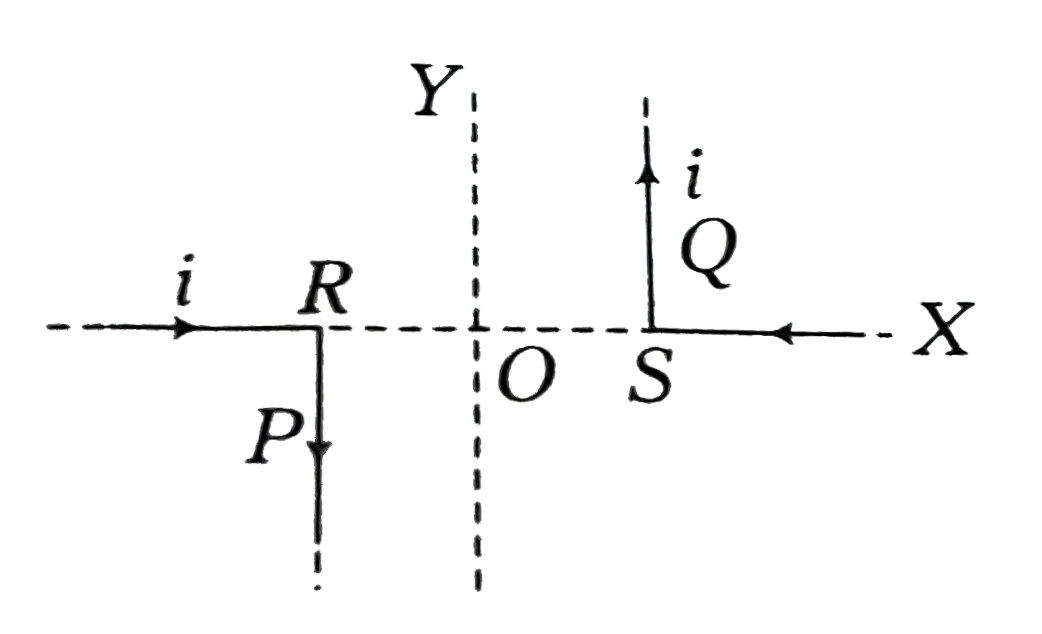
A pair of stationary and infintely long bent wires are placed in the XY planes as shown in fig. The wires carry currents of I=10amperes each as shown . The segments PandQ are parallel to the Y−aξs such that OS=OR=0.02m. Find the magnitude and direction of the magnetic induction at the origin O.
View Solution(i) A pair of stationary and infinitely long bent wires are aplced in the XY- plane as shown.The wires carry currents 10 A each. The segment P and Q are parallel to the Y-axis such as OS =OR = 0.02 m. Find the magnitude field at the origin O
(ii) three long wires carrying 10 A 20 A and 30 A are placed parallel to each other as shown field at P and Q
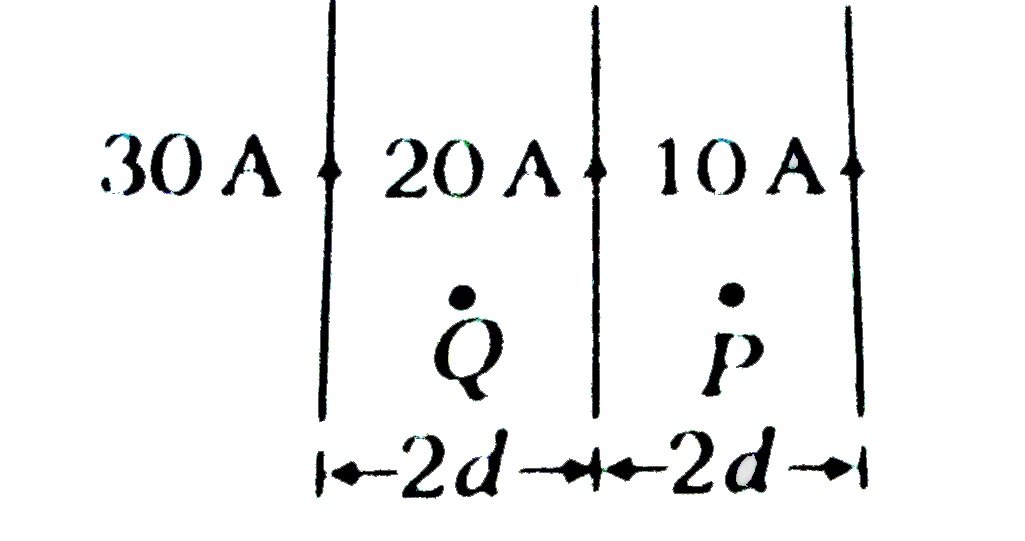
View Solution
Knowledge Check
A wire loop carrying current I is placed in the x-y plane as shown. Magnetic induction at P is
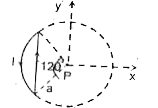 Aμ0I2a(√3π−13)Bμ0I2a(13−π√3)Cμ0I2a(13+√3π)Dμ0I2a(√3π−13)
Aμ0I2a(√3π−13)Bμ0I2a(13−π√3)Cμ0I2a(13+√3π)Dμ0I2a(√3π−13)
A inifinite length current carrying wire is placed in x,y plane parallel to y axis as shown in figure. (All charges projected in region l)AA positively charged particle projected along y axis will get deflected along z axisBA positively charged particle projected along x axis will get deflected along y axisCA negatively charged particle projected along x axis will get deflected along +y axisDA negatively charged particle projected along x axis will get deflected along +z axisA long current wire is bent in the shapes shown in figure. The circular portion has radius R. The magnetic induction at the center of the circular segment is
 A−μ0I4πR[2ˆkp+πˆi],−μ0I4πR[ˆk+(π+1)ˆi],−μ0I4πR[ˆk+ˆj+3π2ˆi]Bμ0I4πR[2ˆkp+πˆi],−μ0I4πR[ˆk+(π+1)ˆi],μ0I4πR[ˆk+ˆj+3π2ˆi]C−μ0I4πR[2ˆkp+πˆi],μ0I4πR[ˆk+(π+1)ˆi],μ0I4πR[ˆk+ˆj+3π2ˆi]Dμ0I4πR[2ˆkp+πˆi],μ0I4πR[ˆk+(π+1)ˆi],μ0I4πR[ˆk+ˆj+3π2ˆi]
A−μ0I4πR[2ˆkp+πˆi],−μ0I4πR[ˆk+(π+1)ˆi],−μ0I4πR[ˆk+ˆj+3π2ˆi]Bμ0I4πR[2ˆkp+πˆi],−μ0I4πR[ˆk+(π+1)ˆi],μ0I4πR[ˆk+ˆj+3π2ˆi]C−μ0I4πR[2ˆkp+πˆi],μ0I4πR[ˆk+(π+1)ˆi],μ0I4πR[ˆk+ˆj+3π2ˆi]Dμ0I4πR[2ˆkp+πˆi],μ0I4πR[ˆk+(π+1)ˆi],μ0I4πR[ˆk+ˆj+3π2ˆi]
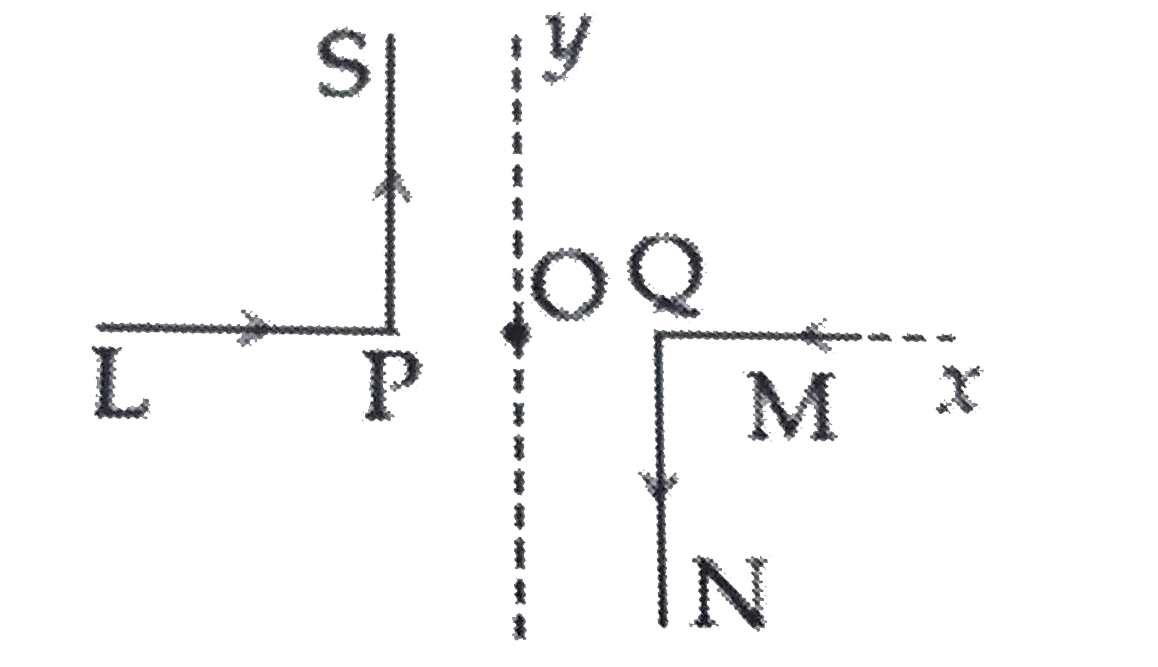
As shown in the figure two infinitely long, identical wires are bent by 90∘ and placed in such a way that the segments LP and QM are along the x-axis , while segments PS and QN are parallel to the Y-axis If OP=OQ=4 cm ,and the magnitude of the magnetic field at O is 10−4 T, and the magnitude of the current in each wire and the direction of the magnetic field at O will be
(μo=4π×10−7NA−2):
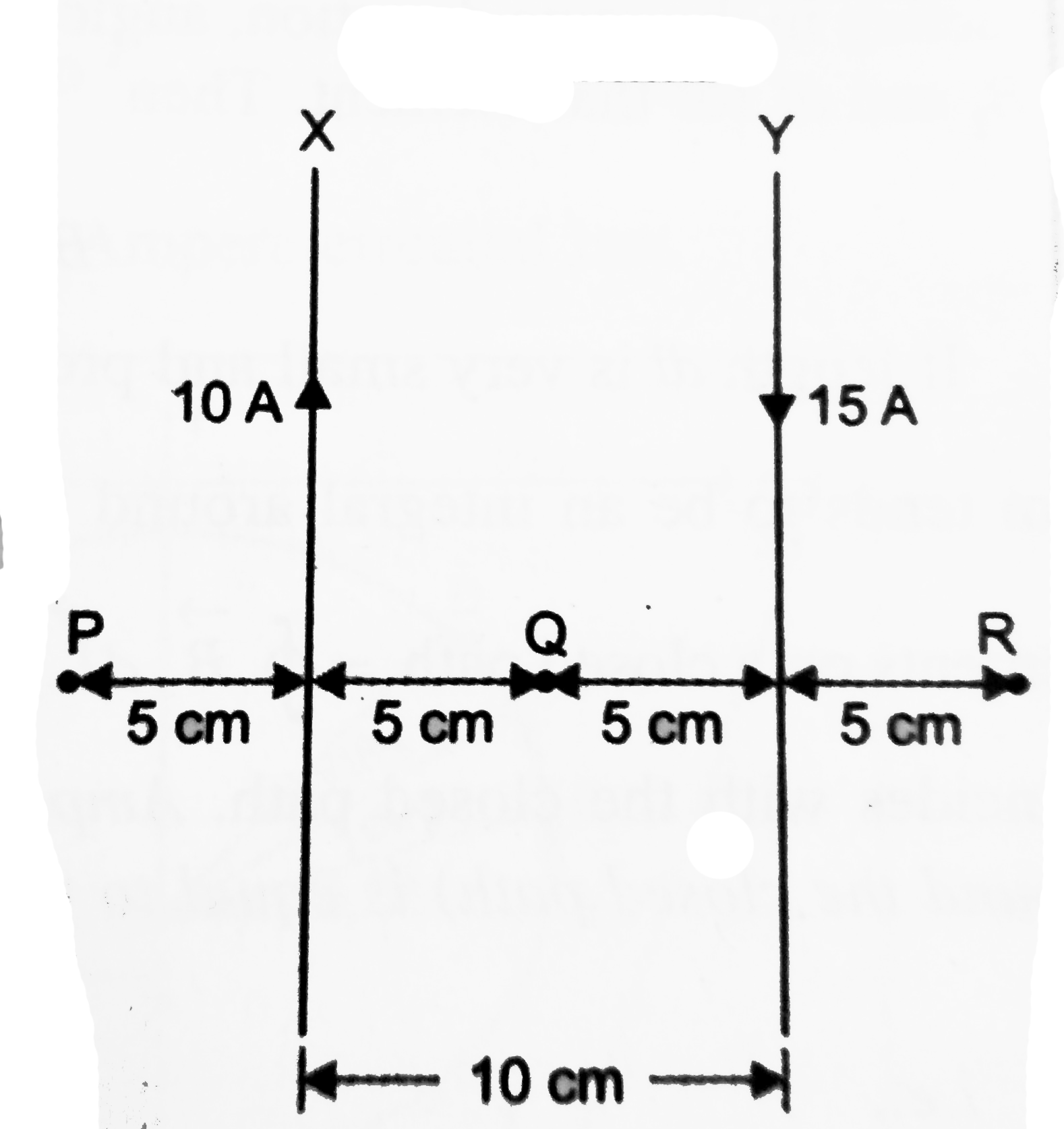
View SolutionThere are two parallel current carrying wires X and Y as shown in figure. Find the magnitude and direction of the magnetic field at points, P, Q and R.
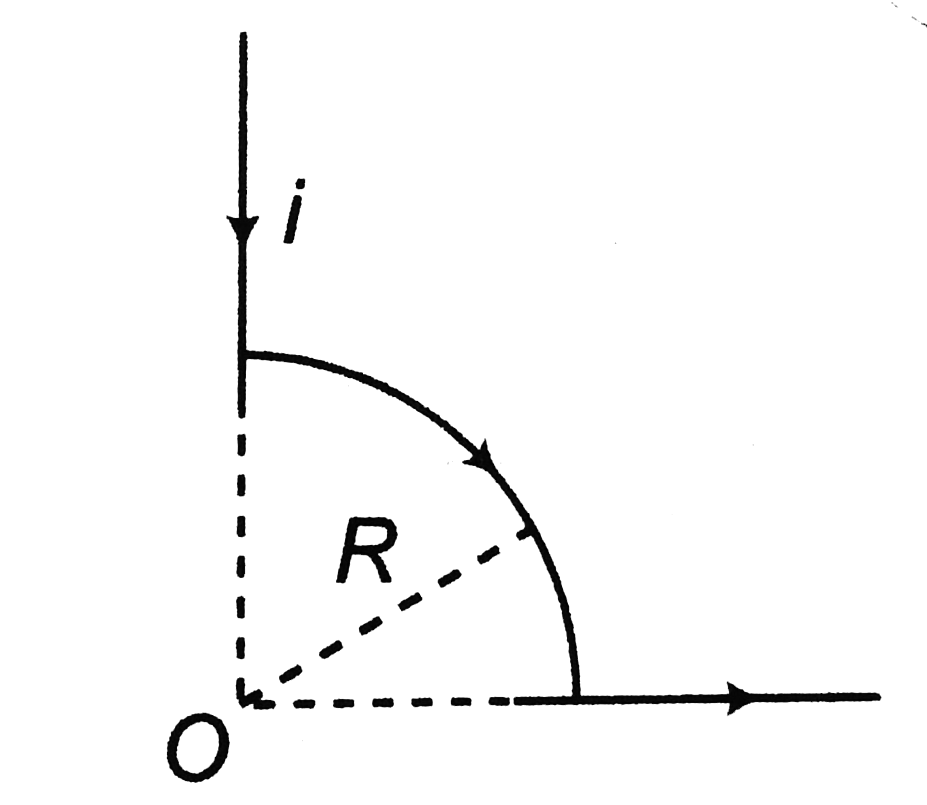
View SolutionThe segment of wire shown in figure carries a current of i=5.0A where the radius of the circular arc is R=3.0cm. Determine the magnitude and direction of the magnetic field at the origin.
View SolutionIn the figure are shown two long parallel current carrying wires I and II. Find the magnitudes and directions of the magnetic field induction at the point P, Q and R in the plane of paper.

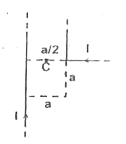
View Solutionone of the two infinitely long wires carrying current I is bent as shown in the adjacent figure. The magnetic induction at C is equal to
View Solution
