Find the force experienced by the wire carrying a current 2A if the ends P and Q of the wire have coordinates (1,2−3)m and (−2,−5,1)m respectively when it is placed in a magnetic field →B=(ˆi+ˆj+ˆk)T
The force acting on the wire is →F=−−→ir21×→B
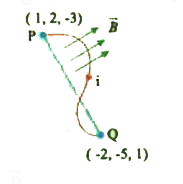
=i(→r2−→r1)×→B
=2(−3ˆi−7ˆj+4ˆk)×(ˆi+ˆj+ˆk)
=2(−11ˆi+7ˆj+4ˆk)N
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - C.U.Q (AMPERE.S CIRCUITAL LAW MAGNETIC FIELD DUE TO STRAIGHT CONDUCTOR )28videos
MOVING CHARGES AND MAGNETISM
- BOOK - NARAYNACHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - C.U.Q (TANGENT GALVANOMETER)8videos
MOVING CHARGES AND MAGNETISM
- BOOK - NARAYNACHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Level -II (H.W)37videos
MOVING CHARGES AND MAGNETISM
- BOOK - NARAYNACHAPTER - MAGNETISM AND MATTEREXERCISE - EXERCISE - 4 (SINGLE ANSWER TYPE QUESTION)17videos
MAGNETISM AND MATTER
- BOOK - NARAYNACHAPTER - NUCLEAR PHYSICSEXERCISE - LEVEL-II-(H.W)9videos
NUCLEAR PHYSICS
Similar Questions
Knowledge Check
- Question 1 - Select One
A "bar" magnet of moment ¯¯¯¯M=ˆi+ˆj is placed in a magnetic field induction →B=3ˆi+4ˆj+4ˆk.
The torque acting on the magnet isA4ˆi−4ˆj+ˆkBˆi+ˆkCˆi−ˆjDˆi+ˆj+ˆk - Question 2 - Select One
A magnet of magnetic moment 50ˆiA−m2 is placed along the x-axis in a magnetic field →B=(0.5ˆi+3.0ˆj)T. The torque acting on the magnet is
A175ˆkN−mB150ˆkN−mC75ˆkN−mD25√37ˆkN−m - Question 3 - Select One
A charge q moves with a velocity 2ms−1 along x-axis in a uniform magnetic field →B=(ˆi+2ˆj+3ˆk) then charge will experience a force
Ain zy planeBalong -y axisCaling +z axisDalong-zaxis
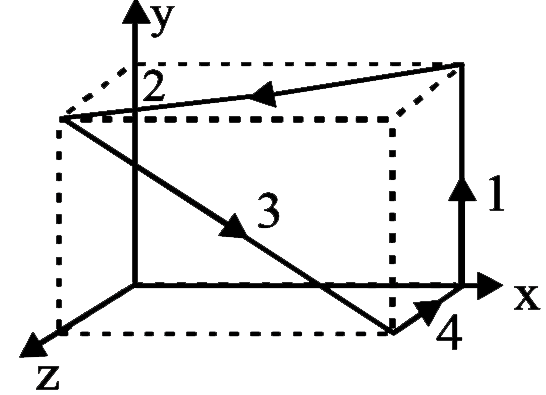
A wire carrying a 10 A current is bent to pass through sides of a cube of side 10 cm as shown in figure. A magnetic field →B=(2ˆi−3ˆj+ˆk)T is present in the region. Then, find
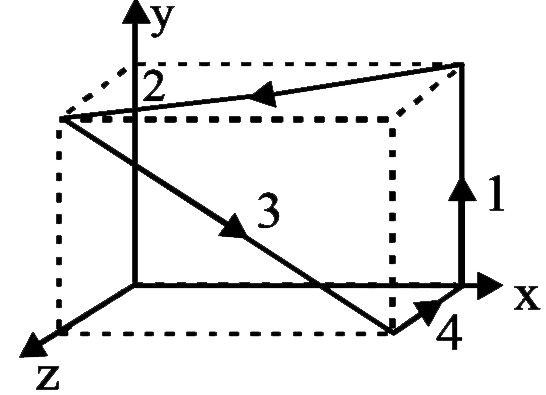
The net torque on the loopView SolutionIf −−→AB=2ˆi+ˆj–3ˆk and the coordinates of A are (1,2,−1), then the coordinates of B are
View SolutionA wire carrying a 10 A current is bent to pass through sides of a cube of side 10 cm as shown in figure. A magnetic field →B=(2ˆi−3ˆj+ˆk)T is present in the region. Then, find
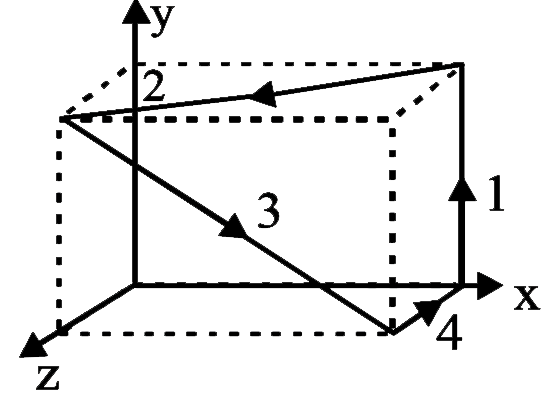
The magnetic moment vector of the loop.View SolutionFind the angle between (→a+→b) and (→a−→b), if →a=(2ˆi−ˆj+3ˆk) and →b=(3ˆi+ˆj+2ˆk).
View SolutionFind the area of the parallelogram whose diagonals are represented by the vectors
(i)→d1=3ˆi+ˆj−2ˆk and →d2=ˆi−3ˆj+4ˆk
(ii) →d1=2ˆi−ˆj+ˆk and →d2=3ˆi+4ˆj−ˆk
(iii) →d1=ˆi−3ˆj+2ˆk and →d2=−ˆi+2ˆj.View Solution