In a series resonant circuit, the ac voltage across resistance R, inductance L and capacitance C are $V_{R} = 4 V, V_{L} = 10 V$ and $V_{C} = 7 V$ respectively. Find the voltage applied to the circuit.

Video Solution

Text Solution

Generated By DoubtnutGPT

To find the voltage applied to the series resonant circuit with the given voltages across the resistor (R), inductor (L), and capacitor (C), we will follow these steps:
Step 1: Identify the given voltages
We have the following voltages:
- Voltage across the resistor, $V_{R} = 4 V$
- Voltage across the inductor, $V_{L} = 10 V$
- Voltage across the capacitor, $V_{C} = 7 V$
Step 2: Understand the phase relationships
In an AC circuit, the voltages across the inductor and capacitor are out of phase with each other. The voltage across the resistor is in phase with the current. Therefore, we can represent these voltages as vectors:
- $V_{R}$ is along the horizontal axis.
- $V_{L}$ is along the vertical axis pointing upwards (inductive reactance).
- $V_{C}$ is along the vertical axis pointing downwards (capacitive reactance).
Step 3: Calculate the net voltage across the inductor and capacitor
Since $V_{L}$ and $V_{C}$ are in opposite directions, we can find the net voltage across them:
$V_{L C} = V_{L} - V_{C} = 10 V - 7 V = 3 V$
Step 4: Construct the right triangle
Now, we can visualize the voltage across the resistor and the net voltage across the inductor and capacitor as a right triangle:
- One side (adjacent) is $V_{R} = 4 V$
- The other side (opposite) is $V_{L C} = 3 V$
Step 5: Apply the Pythagorean theorem
To find the total voltage $V$ applied to the circuit, we can use the Pythagorean theorem:
$V = \sqrt{V_{R}^{2} + V_{L C}^{2}}$
Substituting the values:
$V = \sqrt{(4 V)^{2} + (3 V)^{2}} = \sqrt{16 + 9} = \sqrt{25} = 5 V$
Step 6: Conclusion
The voltage applied to the circuit is:
$5 V$

Updated on:18/9/2024

In a series resonant circuit, the ac, voltage across resistance R, inductance L and capacitance Care 5V, 10V and 10V, respectively. The ac. voltage applied to the circuit will be
A20 V
B10 V
C5 V
D25 V
In a series resonant circuit, the $A C$ voltage across resistance $R$ , inductance $L$ , and capacitance $C$ are $5 V, 10 V$ and $10 V$ respectively. The $A C$ voltage applied to the circuit will be
A $20 V$
B $10 V$
C $5 V$
D $25 V$
In the given circuit the R.M.S values of voltages across the capacitor C, inductor L and resistor $R_{1}$ are 12V, 10V and 5 V respectively. Then the peak voltage across $R_{2}$ is

A $7 \sqrt{2} V$
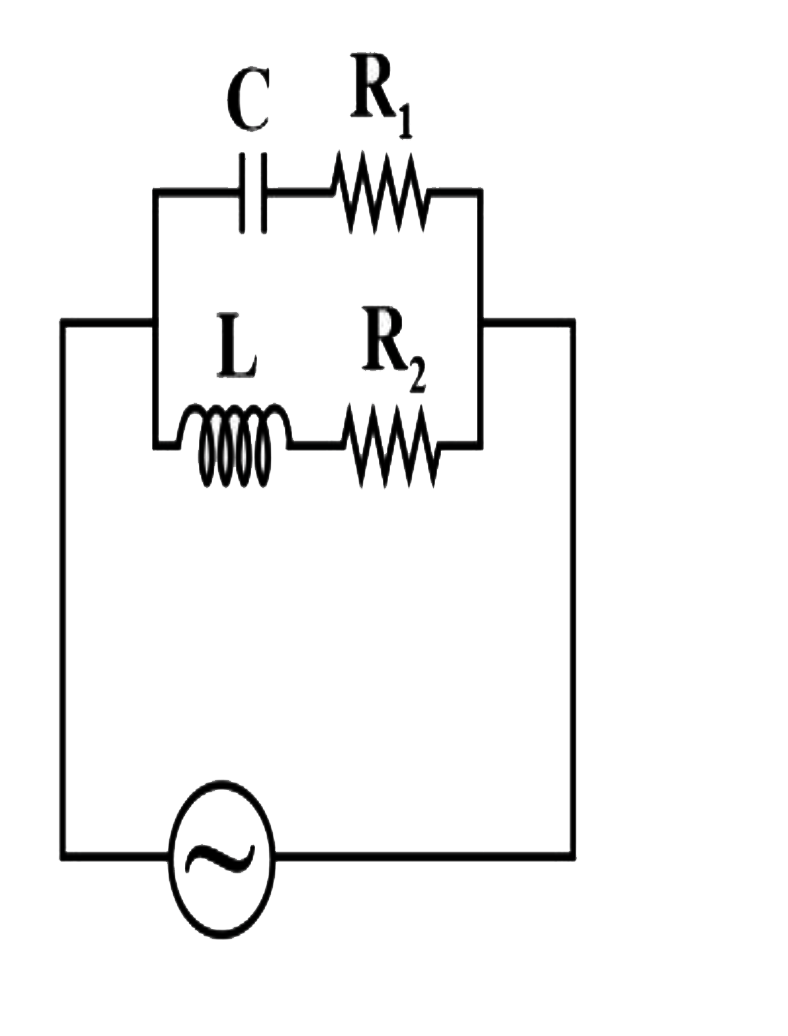B $\sqrt{69} V$
C $\sqrt{138} V$
Dnone of these