Find the velocity of image w.r.t. ground.
For the velocity component along the principle axis
(VIM)=−v2u2(Vom)II
Apply mirror equation:
1v+1u=1f⇒1v+1−20=1−30
⇒ v = +60 cm ⇒m=−vu=−60−20=3
Shortcut solution:
m=ff−u=−30(−30)−(−20)=+3
v=−μ=−(3)(−20)=+60cm
since mirror is at rest (given that) :
(VIM)II=−(60−20)2(5)=-45m/s
⇒¯¯¯¯¯¯VIG=¯¯¯¯¯¯¯VIM+¯¯¯¯¯¯¯VMG
⇒=−45+0=-45 m/s
That means image approaches the mirror with velocity 45 m/s
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRAUMENTS BOOK - NARAYNACHAPTER - RAY OPTICS AND OPTICAL INSTRAUMENTS EXERCISE - CUQ (REFLECTION)
9 Videos
- RAY OPTICS AND OPTICAL INSTRAUMENTS BOOK - NARAYNACHAPTER - RAY OPTICS AND OPTICAL INSTRAUMENTS EXERCISE - CUQ (REFRECTION)
28 Videos
- NUCLEI BOOK - NARAYNACHAPTER - NUCLEI EXERCISE - ASSERTION & REASON
5 Videos
- SEMI CONDUCTOR DEVICESBOOK - NARAYNACHAPTER - SEMI CONDUCTOR DEVICESEXERCISE - Level-II (H.W)
36 Videos
Similar Questions
Three blocks shown in move vertically with constant velocities The relative velocity of w.r.t C is 100m/s upward and the relative velocity of B w.r.t A is 50m/s downward. All the string are ideal The velocity of C with respect to ground is 125/x calculate x
.
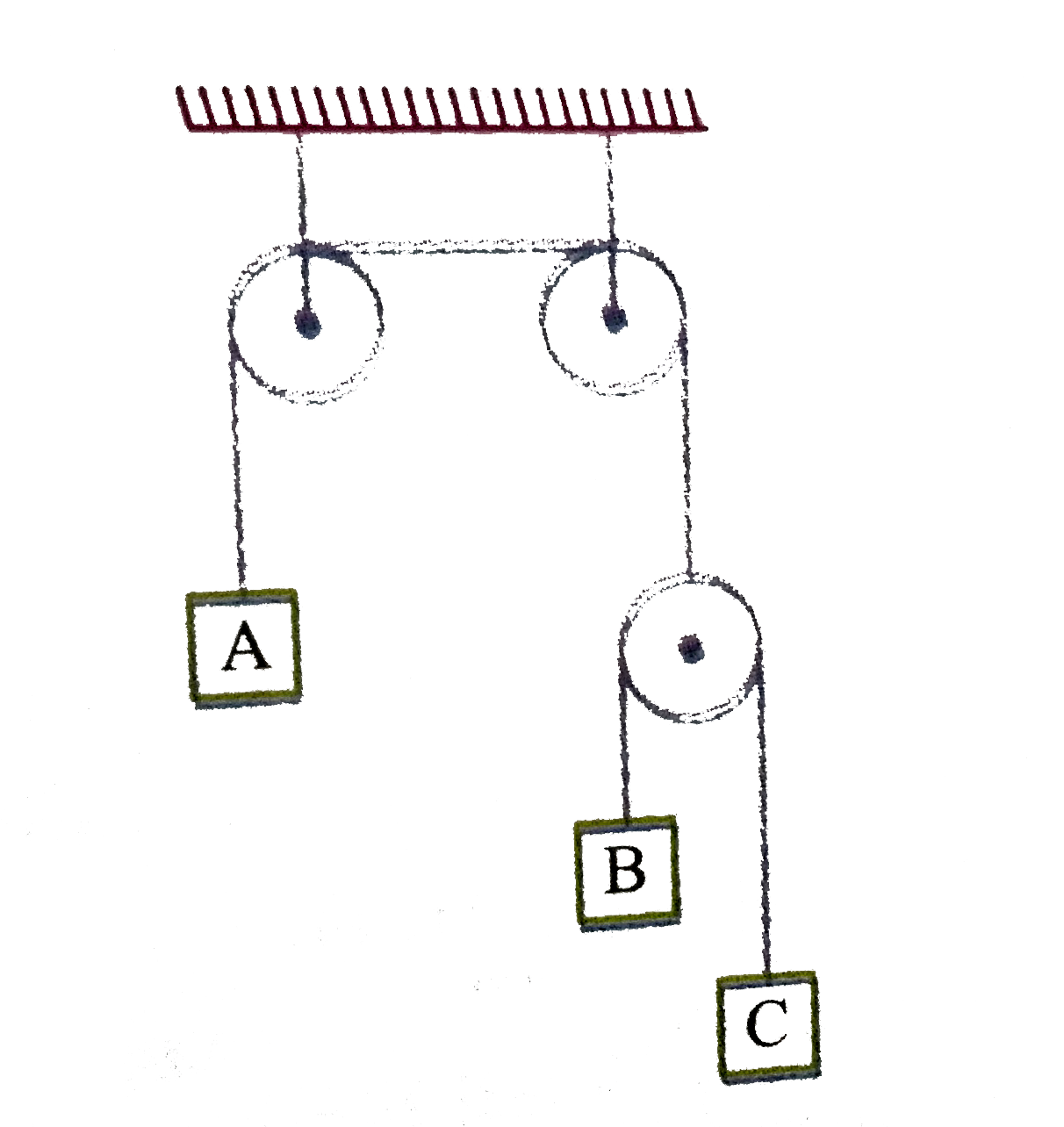View SolutionFind the acceleration of C w.r.t. ground.
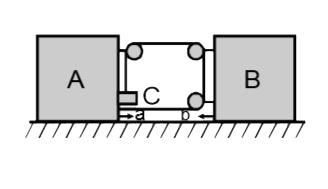
View Solution
Knowledge Check
The velocity of image w.r.t ground in the below figure is
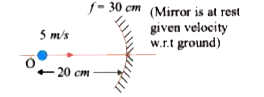A45 m/s and approaches the mirrorB45 m/s and moves away from the mirrorC60 m/s and approaches the mirrorD60 m/s and moves away from the mirrorWe know that when a boat travels in water, its net velocity w.r.t. ground is the vector sum of two velocities. First is the velocity of boat itself in river and other is the velocity of water w.r.t. ground. Mathematically:
→vboat=→vboat,water+→vwater.
Now given that velocity of water w.r.t. ground in a river is u. Width of the river is d.
A boat starting from rest aims perpendicular to the river with an acceleration of a = 5t, where t is time. The boat starts from point (1,0) of the coordinate system as shown in figure. Assume SI units.A(3d/5)1/3B(6d/5)1/3C(6d/5)1/2D(2d/3)1/3We know that when a boat travels in water, its net velocity w.r.t. ground is the vector sum of two velocities. First is the velocity of boat itself in river and other is the velocity of water w.r.t. ground. Mathematically:
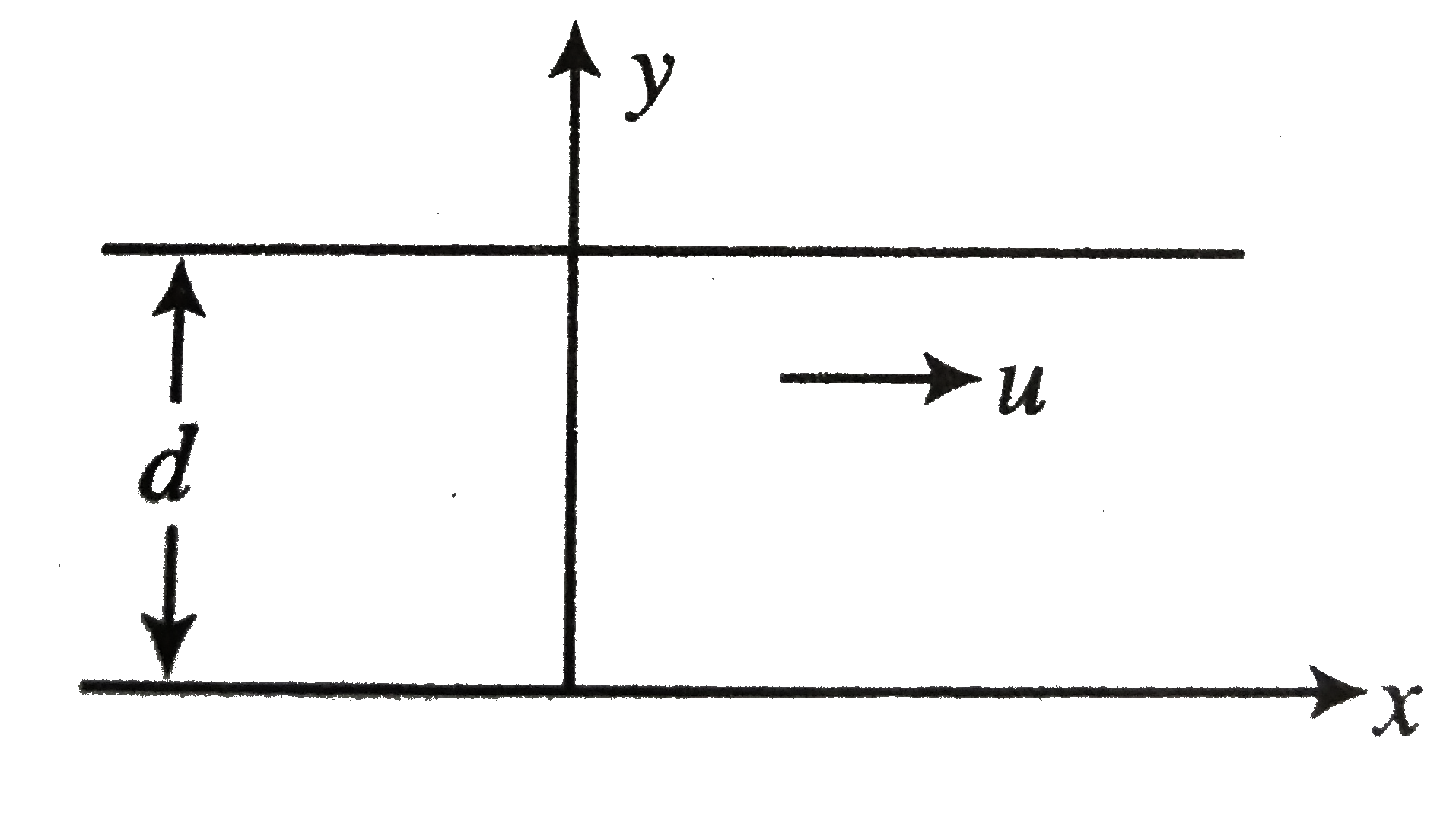
→vboat=→vboat,water+→vwater.
Now given that velocity of water w.r.t. ground in a river is u. Width of the river is d.
A boat starting from rest aims perpendicular to the river with an acceleration of a = 5t, where t is time. The boat starts from point (1,0) of the coordinate system as shown in figure. Assume SI units.Ax−1=u(3y5)1/3Bx=u(6y5)1/3Cx=1=u(6y5)1/3DNone of these
We know that when a boat travels in water, its net velocity w.r.t. ground is the vector sum of two velocities. First is the velocity of boat itself in river and other is the velocity of water w.r.t. ground. Mathematically:
→vboat=→vboat,water+→vwater.
Now given that velocity of water w.r.t. ground in a river is u. Width of the river is d.
A boat starting from rest aims perpendicular to the river with an acceleration of a = 5t, where t is time. The boat starts from point (1,0) of the coordinate system as shown in figure. Assume SI units. Find time taken by him to across the river.
View SolutionWe know that when a boat travels in water, its net velocity w.r.t. ground is the vector sum of two velocities. First is the velocity of boat itself in river and other is the velocity of water w.r.t. ground. Mathematically:
→vboat=→vboat,water+→vwater.
Now given that velocity of water w.r.t. ground in a river is u. Width of the river is d.
A boat starting from rest aims perpendicular to the river with an acceleration of a = 5t, where t is time. The boat starts from point (1,0) of the coordinate system as shown in figure. Assume SI units.
View SolutionWe know that when a boat travels in water, its net velocity w.r.t. ground is the vector sum of two velocities. First is the velocity of boat itself in river and other is the velocity of water w.r.t. ground. Mathematically:
→vboat=→vboat,water+→vwater.
Now given that velocity of water w.r.t. ground in a river is u. Width of the river is d.
A boat starting from rest aims perpendicular to the river with an acceleration of a = 5t, where t is time. The boat starts from point (1,0) of the coordinate system as shown in figure. Assume SI units.
View SolutionA bus appears to move northwards at a speed of 20√3 km h−1 . To a man diving his car eastwards with speed 20 km h −1. Find the velocity of the bus w.r.t ground.
View SolutionWe know that when a boat travels in water, its net velocity w.r.t. ground is the vector sum of two velocities. First is the velocity of boat itself in river and other is the velocity of water w.r.t. ground. Mathematically:
→vboat=→vboat,water+→vwater.
Now given that velocity of water w.r.t. ground in a river is u. Width of the river is d.
A boat starting from rest aims perpendicular to the river with an acceleration of a = 5t, where t is time. The boat starts from point (1,0) of the coordinate system as shown in figure. Assume SI units.
View Solution