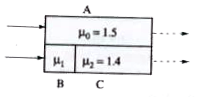
Consider slabs of three media A, B and C arranged as shown in figure R.I. of A is 1.5 and that of C is 1.4. If the number of waves in A is equal to the number of waves in the combination of B and C then refractive index of B is:
$Consider slabs of three media A, B and C arranged as shown in figure R.I. of A is 1.5 and that of C is 1.4. If the number of waves in A is equal to the number of waves in the combination of B and C then refractive index of B is:$

Text Solution

Verified by Experts

$N_{A} = N_{B} + N_{C}$
$\frac{x_{A}}{λ_{A}} = \frac{x_{B}}{λ_{B}} + \frac{x_{C}}{λ_{C}}$
$\frac{x_{A} μ_{A}}{λ_{0}} = \frac{x_{B} μ_{B}}{λ_{0}} + \frac{x_{C} μ_{C}}{λ_{0}}$
3x $\times 1.5$ =x $\times μ_{B} +$ 2x $\times$ 1.4
$∴ M u_{B}$ =1.7

Updated on:21/07/2023

|

Class 12 PHYSICS GEOMETRICAL OPTICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Consider slabs of three media A,B, and C. Arragned as shown inn figure . R.I of A is 1.5 and that of C is 1.4. If the number of waves in the combination B and C then refractive index of B is

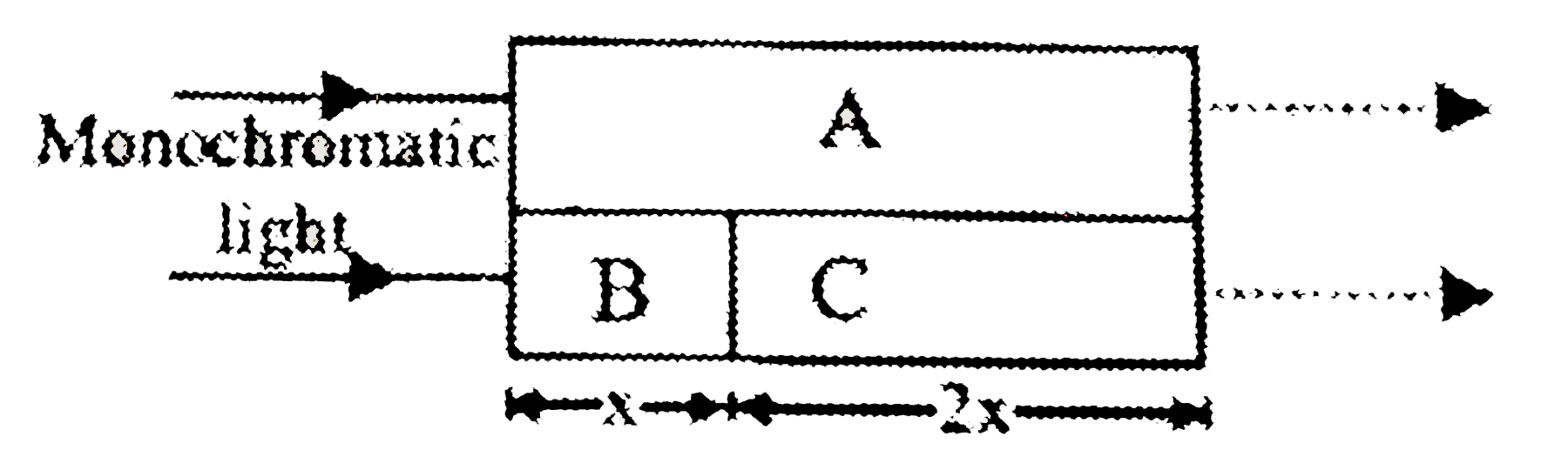A1.4
B1.5
C1.6
D1.7
A slab of transparent material is made as shown in Fig. Monochromatic parallel beams of light are normally incident on the slab. The thickness of $C$ is twice the thickness of $B$ . If the number of waves in A = number of waves in combination of $B and C$ , then the refractive index of $B$ is :
.
A1.33
B1.8
C1.6
D1.6
Three progressive waves $A, B$ and $C$ are shown in figure. With respect to wave $A$
.
AThe wave $C$ lags behind in phase by $π / 2$ and $B$ leads by $π / 2$
BThe wave $C$ leads in phase by $π$ and $B$ lags behind by $π$
CThe wave $C$ leads in phase by $π / 2$ and $B$ lags behind by $π / 2$
DThe wave $C$ lags behind in phase by $π$ and $B$ leads by $π$

NARAYNA-RAY OPTICS AND OPTICAL INSTRAUMENTS -EXERCISE- 4 One or more than one correct answer type

Home
Ask Doubt
Profile