A ray of light incident on the horizontal surface of a glass slab at an angle of incidence ‘i’just grazes the adjacent vertical surface after reflection. Compute the critical angle and refractive index of glass
To solve the problem, we need to derive the critical angle and the refractive index of the glass slab based on the given conditions. Here’s the step-by-step solution:
Step 1: Understanding the Situation
We have a glass slab where a ray of light is incident at an angle i on the horizontal surface. After reflection, the ray just grazes the adjacent vertical surface. This means that the angle of incidence at the vertical surface is equal to the critical angle c for total internal reflection.
Step 2: Applying Snell's Law
When the light ray travels from air (refractive index n1=1) into glass (refractive index n2=μ), we can apply Snell's law:
n1sin(i)=n2sin(r)
where r is the angle of refraction inside the glass.
Step 3: Condition for Grazing Reflection
Since the ray just grazes the vertical surface, it means that the angle of refraction r at the glass-air interface is 90∘ (as it is parallel to the surface). Thus, sin(r)=sin(90∘)=1.
Step 4: Finding the Critical Angle
At the critical angle c, we have:
sin(c)=n1n2=1μ
This gives us the relationship for the critical angle.
Step 5: Relating Angles
From the geometry of the situation, we can also relate the angles:
- The angle of incidence i and the angle of refraction r are related through the triangle formed at the interface. Since r=90∘−c, we can write:
i+c=90∘
Thus, r=90∘−c.
Step 6: Using the Relationship in Snell's Law
Substituting r=90∘−c into Snell's law gives:
1⋅sin(i)=μ⋅sin(90∘−c)=μ⋅cos(c)
From this, we can express sin(i) as:
sin(i)=μcos(c)
Step 7: Expressing cos(c) in Terms of sin(c)
Using the identity cos(c)=√1−sin2(c), we can substitute sin(c)=1μ:
cos(c)=√1−(1μ)2=√μ2−1μ2
Thus, we can rewrite sin(i):
sin(i)=μ⋅√μ2−1μ2=√μ2−1
Step 8: Squaring Both Sides
Squaring both sides gives:
sin2(i)=μ2−1
Rearranging gives:
μ2=1+sin2(i)
Thus, the refractive index μ is:
μ=√1+sin2(i)
Step 9: Finding the Critical Angle
Now substituting back to find the critical angle:
sin(c)=1μ=1√1+sin2(i)
Thus, the critical angle c is:
c=sin−1⎛⎜
⎜⎝1√1+sin2(i)⎞⎟
⎟⎠
Final Answers
- The refractive index of glass is:
μ=√1+sin2(i)
- The critical angle is:
c=sin−1⎛⎜
⎜⎝1√1+sin2(i)⎞⎟
⎟⎠
We have a glass slab where a ray of light is incident at an angle i on the horizontal surface. After reflection, the ray just grazes the adjacent vertical surface. This means that the angle of incidence at the vertical surface is equal to the critical angle c for total internal reflection.
When the light ray travels from air (refractive index n1=1) into glass (refractive index n2=μ), we can apply Snell's law:
n1sin(i)=n2sin(r)
where r is the angle of refraction inside the glass.
Since the ray just grazes the vertical surface, it means that the angle of refraction r at the glass-air interface is 90∘ (as it is parallel to the surface). Thus, sin(r)=sin(90∘)=1.
At the critical angle c, we have:
sin(c)=n1n2=1μ
This gives us the relationship for the critical angle.
From the geometry of the situation, we can also relate the angles:
- The angle of incidence i and the angle of refraction r are related through the triangle formed at the interface. Since r=90∘−c, we can write:
i+c=90∘
Thus, r=90∘−c.
Substituting r=90∘−c into Snell's law gives:
1⋅sin(i)=μ⋅sin(90∘−c)=μ⋅cos(c)
From this, we can express sin(i) as:
sin(i)=μcos(c)
Using the identity cos(c)=√1−sin2(c), we can substitute sin(c)=1μ:
cos(c)=√1−(1μ)2=√μ2−1μ2
Thus, we can rewrite sin(i):
sin(i)=μ⋅√μ2−1μ2=√μ2−1
Squaring both sides gives:
sin2(i)=μ2−1
Rearranging gives:
μ2=1+sin2(i)
Thus, the refractive index μ is:
μ=√1+sin2(i)
Now substituting back to find the critical angle:
sin(c)=1μ=1√1+sin2(i)
Thus, the critical angle c is:
c=sin−1⎛⎜
⎜⎝1√1+sin2(i)⎞⎟
⎟⎠
- The refractive index of glass is:
μ=√1+sin2(i)
- The critical angle is:
c=sin−1⎛⎜
⎜⎝1√1+sin2(i)⎞⎟
⎟⎠
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - RAY OPTICS AND OPTICAL INSTRAUMENTS EXERCISE - CUQ (REFLECTION)9videos
RAY OPTICS AND OPTICAL INSTRAUMENTS
- BOOK - NARAYNACHAPTER - RAY OPTICS AND OPTICAL INSTRAUMENTS EXERCISE - CUQ (REFRECTION)28videos
RAY OPTICS AND OPTICAL INSTRAUMENTS
- BOOK - NARAYNACHAPTER - NUCLEI EXERCISE - ASSERTION & REASON5videos
NUCLEI
- BOOK - NARAYNACHAPTER - SEMI CONDUCTOR DEVICESEXERCISE - Level-II (H.W)36videos
SEMI CONDUCTOR DEVICES
Similar Questions
A ray of light incident on the horizontal surface of a glass slab at 70∘ just grazes the adjacent vertical surface after refraction. Complete the critical angle and refractive index of glass.
View SolutionConsider the figure given below. A ray of light is incident on one of the horizontal surfaces of glass slab at an angle of 60∘ and it just grazes along the adjacent vertical sides after refraction. Calculate the critical angle .
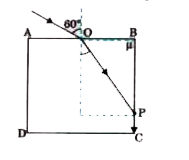 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A ray of light is incident on the surface of a glass plate of thickness t. If the angle of incidence θ is small, the emerging ray would be displaced side ways by an amount
(Take n = refractive index of glass)Atθn/(n+1)Btθ(n−1)/nCtθn/(n−1)Dtθ(n+1)/n - Question 2 - Select One
A ray of light is incident on the surface of a glass plate of thickness t. I fthe angle of incidence θ is small, the emerging ray would be displaced side ways by an amount
[Taken = refractive index of glass)Atθn/(n+1)Btθ(n−1)/nCtθn/(n−1)Dtθ(n+1)/n - Question 3 - Select One
A ray of light is incident on the interface between water and glass at an angle i and refracted parallel to the water surface, then value of μg will be
 A(4/3)siniB1siniC43D1
A(4/3)siniB1siniC43D1
A ray of light makes an angle of 40∘ with the surface S1 of the glass slab. Its angle of incidence will be ……..
View SolutionA ray of light makes an angle of 50∘ with the surface S1 of the glass slab. Its angle of incidence will be ____
View SolutionA ray of light is incident on the surface of a glass plate at an angle of incidence equal to Brewster's angle ϕ. If μ represents the refractive index of glass with respect to air, then the angle between reflected and refracted rays is
View SolutionA ray of light makes an angle of 50∘ with the surface S1 of the glass slab. Its angle of incidence will be ____
View SolutionA ray of light is incident on the interface between water and glass at an angle i and refracted parallel to the water surface, then value of μg will be
 View Solution
View Solution

