A cubic container is filled with a liquid whose refractive index increases linearly from top to bottom. Which of the following represents the path of a ray of light inside the liquid ?

Since, the refractive index is changing, the light cannot travel in a straight line in the liquid as shown in options (3) and (4).
Intitially it will bend towards normal and after reflecting from the bottom it will bend away from the norami so (1) is correct answer.
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRAUMENTS BOOK - NARAYNACHAPTER - RAY OPTICS AND OPTICAL INSTRAUMENTS EXERCISE - CUQ (REFLECTION)
9 Videos
- RAY OPTICS AND OPTICAL INSTRAUMENTS BOOK - NARAYNACHAPTER - RAY OPTICS AND OPTICAL INSTRAUMENTS EXERCISE - CUQ (REFRECTION)
28 Videos
- NUCLEI BOOK - NARAYNACHAPTER - NUCLEI EXERCISE - ASSERTION & REASON
5 Videos
- SEMI CONDUCTOR DEVICESBOOK - NARAYNACHAPTER - SEMI CONDUCTOR DEVICESEXERCISE - Level-II (H.W)
36 Videos
Similar Questions
If a glass prism is kept in a liquid of the same refractive index as that of glass, will the ray of light bend (Fig. B)? Complete the path of the ray of light.

View SolutionTwo plane mirrors M1 and M2, placed at right angles, form two sides of a container. Mirror M1 is inclined at an angle θ0 to the horizontal. A light ray AB is incident normally onM1. Now the container is filled with a liquid of refractive index μ so that the ray is first refracted, then reflected at M1. The ray is next reflected at M2 and then comes out of the liquid surface making an angle θ with the normal to the liquid surface. Find θ.
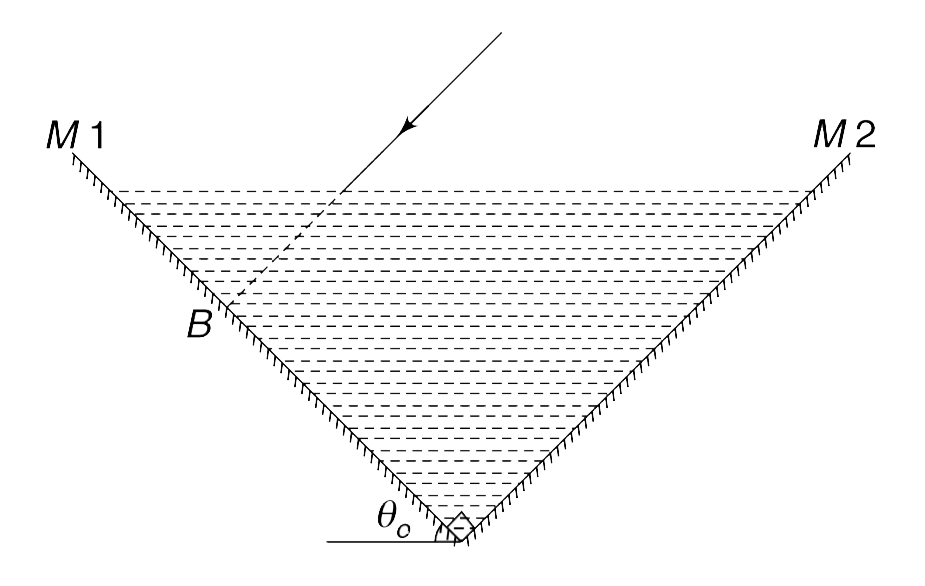
View Solution
Knowledge Check
A small coin is resting on the bottom of a beaker filled with a liquid. A ray of light from the coin travels upto the surface of the liquid and moves along its surface How fast is the light travelling the liquid ?
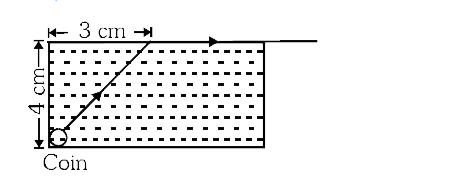
A1.8×108ms−1B2.4×108ms−1C3.0×108ms−1D1.2×108ms−1A metal coin at the bottom of a beaker filled with a liquid of refractive index 4/3 to height of 6cm. To an observer looking from above the surface of the liquid, coin will appear at a depth of (consider paraxial rays).
A7.5cmB6.75cmC4.5cmD1.5cm
(i) Define refractive index of a medium.
(ii) In the following ray diagram, calculate the speed of light in the liquid of unknown refractive index.
View SolutionA small illuminated bulb is at the bottom of a tank, containing a liquid of refractive index μ upto a height H. Find the expression for the diameter of an opaque disc, floating symmetrically on the liquid surface in order to cut- off the light from the bulb.
View SolutionA small illuminated bulb is at the bottom of a tank, containing a liquid of refractive index μ upto a height H. Find the expression for the diameter of an opaque disc, floating symmetrically on the liquid surface in order to cut- off the light from the bulb.
View SolutionA small coin is resting on the bottom of a beaker filled with a liquid. A ray of light from the coin travels upto the surface of the liquid and moves along its surface How fast is the light travelling the liquid ?

View SolutionA jar 15cm long is filled with a transparent liquid. When viewed from the top, its bottom appears to be 12cm below. What is the refractive index of the liquid ?
View SolutionA metal coin at the bottom of a beaker filled with a liquid of refractive index 4/3 to height of 6cm. To an observer looking from above the surface of the liquid, coin will appear at a depth of (consider paraxial rays).
View Solution
