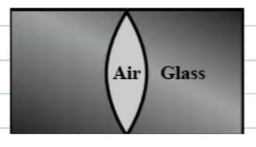
As shown in figure a spherical air lens of radii $R_{1} = R_{2}$ = 10cm is cut in a glass ( $μ$ = 1.5) cylinder. Determine the focal length and nature of air lens. If a liquid of refractive index 2 is filled in the lens, what will happen to its focal length and nature?
$As shown in figure a spherical air lens of radii R(1)=R(2)= 10cm is cut in a glass (mu= 1.5) cylinder. Determine the focal length and nature of air lens. If a liquid of refractive index 2 is filled in the lens, what will happen to its focal length and nature?$

Text Solution

Verified by Experts

According to lens-maker’s formula
$\frac{1}{f} = (μ - 1) [\frac{1}{R_{1}} - \frac{1}{R_{2}}]$ with $μ = \frac{μ_{L}}{μ_{M}}$
Initially, $μ = \frac{μ_{A}}{μ_{G}} = \frac{1}{(3 / 2)} = \frac{2}{3}, R_{1} = + 10 c m$
So $\frac{1}{f} = [\frac{2}{3} - 1] [\frac{1}{+ 10} - \frac{1}{- 10}] = - \frac{2}{30}$ i.e., f=-15cm
ie. the air lens in glass behaves as divergent lens of focal length 15cm.
When the liquid of p = 2 is filled in the air cavity,
$μ = \frac{μ_{L}}{μ_{M}} = \frac{2}{1.5} = \frac{4}{3}$
SO that now $\frac{1}{f^{.}} = [\frac{4}{3} - 1] [\frac{1}{10} - \frac{1}{- 10}] = \frac{2}{30}$
f. = 15 cm ie. the liquid lens in glass will behave as a convergent lens of focal length 15cm.

Updated on:21/07/2023

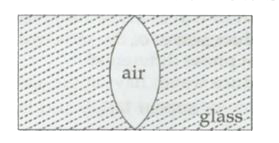
In the figure, an air lens is cut a cylinder of glass of refractive index 1.5 . The nature of the lens is

Adiveriging
Bconverging
Cneither diverging nor converging
Dnone of these
A lens of refractive index n is put in a liquid of refractive index $n'$ . If focal length of lens in air is $f$ , its focal length in liquid will be.
A $\frac{f n' (n - 1)}{n' - n}$
B $\frac{f (n' - 1)}{n' (n - 1)}$
C $\frac{n' (n - 1)}{f (n' - 1)}$
D $\frac{f n' n}{n - n'}$
A lens of refractive index n is put in a liquid of refractive index $n'$ . If focal length of lens in air is $f$ , its focal length in liquid will be.
A $\frac{- f n' (n - 1)}{n' - n}$
B $\frac{- f (n' - n)}{n' (n - 1)}$
C $\frac{- n' (n - 1)}{f (n' - n)}$
D $\frac{f n' n}{n - n'}$