A plot of modulus of image distance versus object distance for a spherical mirror is a:
Straight Line
Circle
Parabola
Hyperbola
The correct Answer is:D
To solve the question regarding the plot of the modulus of image distance versus object distance for a spherical mirror, we will follow these steps:
Step 1: Understand the Mirror Formula
The mirror formula relates the object distance (u), image distance (v), and focal length (f) of a spherical mirror:
1v+1u=1f
From this, we can express v in terms of u:
1v=1f−1u
This can be rearranged to:
v=fuu−f
Step 2: Analyze the Equation
The equation v=fuu−f indicates that as u approaches f, v approaches infinity. This suggests a hyperbolic relationship because the image distance v will not be defined when u=f.
Step 3: Consider the Modulus
Since the question asks for the modulus of the image distance, we will consider |v|. The relationship remains:
|v|=∣∣∣fuu−f∣∣∣
This means that the graph will still exhibit hyperbolic characteristics, as the absolute value does not change the nature of the relationship.
Step 4: Plot the Graph
To plot the graph of |v| versus u:
- When u=0, |v| is undefined (as v approaches infinity).
- When u=f, |v| is also undefined (as v approaches infinity).
- For values of u less than f, |v| will be negative, but since we are taking the modulus, it will be positive.
- For values of u greater than f, |v| will be positive.
Step 5: Conclusion
The plot of |v| versus u will resemble a hyperbola, with branches in the first and second quadrants, indicating that as the object distance increases or decreases away from the focal point, the image distance behaves hyperbolically.
Final Answer
The plot of the modulus of image distance versus object distance for a spherical mirror is a hyperbola.
---
The mirror formula relates the object distance (u), image distance (v), and focal length (f) of a spherical mirror:
1v+1u=1f
From this, we can express v in terms of u:
1v=1f−1u
This can be rearranged to:
v=fuu−f
The equation v=fuu−f indicates that as u approaches f, v approaches infinity. This suggests a hyperbolic relationship because the image distance v will not be defined when u=f.
Since the question asks for the modulus of the image distance, we will consider |v|. The relationship remains:
|v|=∣∣∣fuu−f∣∣∣
This means that the graph will still exhibit hyperbolic characteristics, as the absolute value does not change the nature of the relationship.
To plot the graph of |v| versus u:
- When u=0, |v| is undefined (as v approaches infinity).
- When u=f, |v| is also undefined (as v approaches infinity).
- For values of u less than f, |v| will be negative, but since we are taking the modulus, it will be positive.
- For values of u greater than f, |v| will be positive.
The plot of |v| versus u will resemble a hyperbola, with branches in the first and second quadrants, indicating that as the object distance increases or decreases away from the focal point, the image distance behaves hyperbolically.
The plot of the modulus of image distance versus object distance for a spherical mirror is a hyperbola.
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRAUMENTS BOOK - NARAYNACHAPTER - RAY OPTICS AND OPTICAL INSTRAUMENTS EXERCISE - EXERCISE-2 (C.W)(REFRACTION)
20 Videos
- RAY OPTICS AND OPTICAL INSTRAUMENTS BOOK - NARAYNACHAPTER - RAY OPTICS AND OPTICAL INSTRAUMENTS EXERCISE - EXERCISE-2 (C.W)(REFRACTION THROUGH SPHERICAL SURFACES )
29 Videos
- RAY OPTICS AND OPTICAL INSTRAUMENTS BOOK - NARAYNACHAPTER - RAY OPTICS AND OPTICAL INSTRAUMENTS EXERCISE - EXERCISE-1 (H.W)( OPTICAL INSTRUMENTS( TELESCOPES ) )
3 Videos
- NUCLEI BOOK - NARAYNACHAPTER - NUCLEI EXERCISE - ASSERTION & REASON
5 Videos
- SEMI CONDUCTOR DEVICESBOOK - NARAYNACHAPTER - SEMI CONDUCTOR DEVICESEXERCISE - Level-II (H.W)
36 Videos
Similar Questions
Knowledge Check
The minimum distance between the object and its real image for a concave mirror is
AfB2fC4fDzeroThe graph showing correctly the variation of image distance (v) as a function of object distance (u) in case of a concave mirror is
A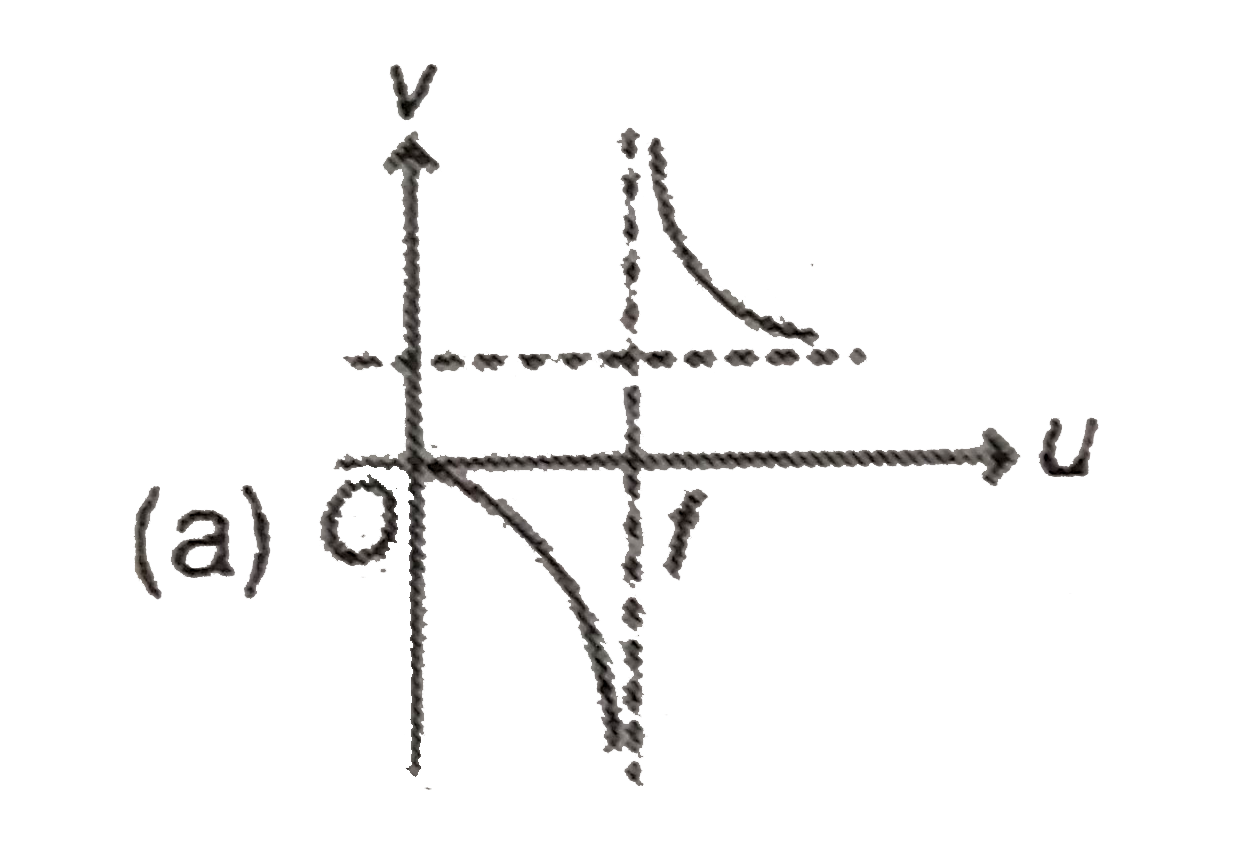 B
B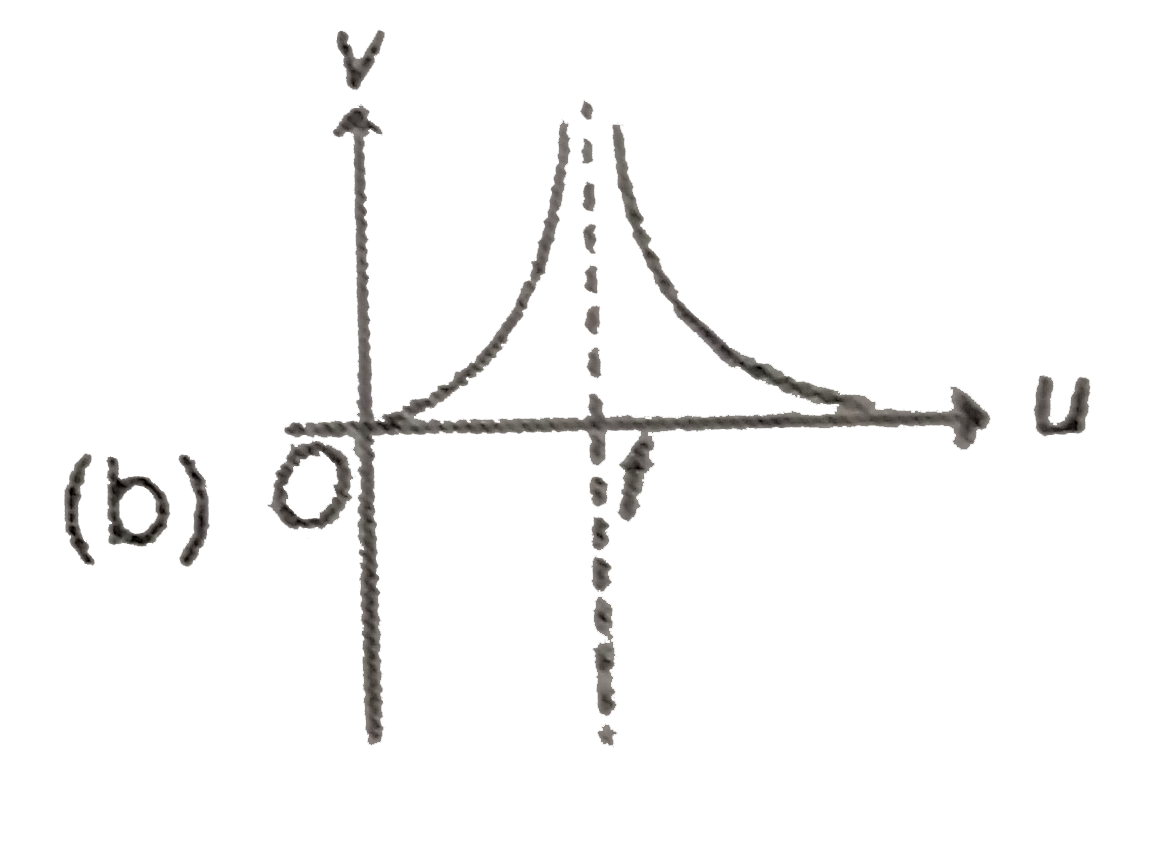 C
C D
D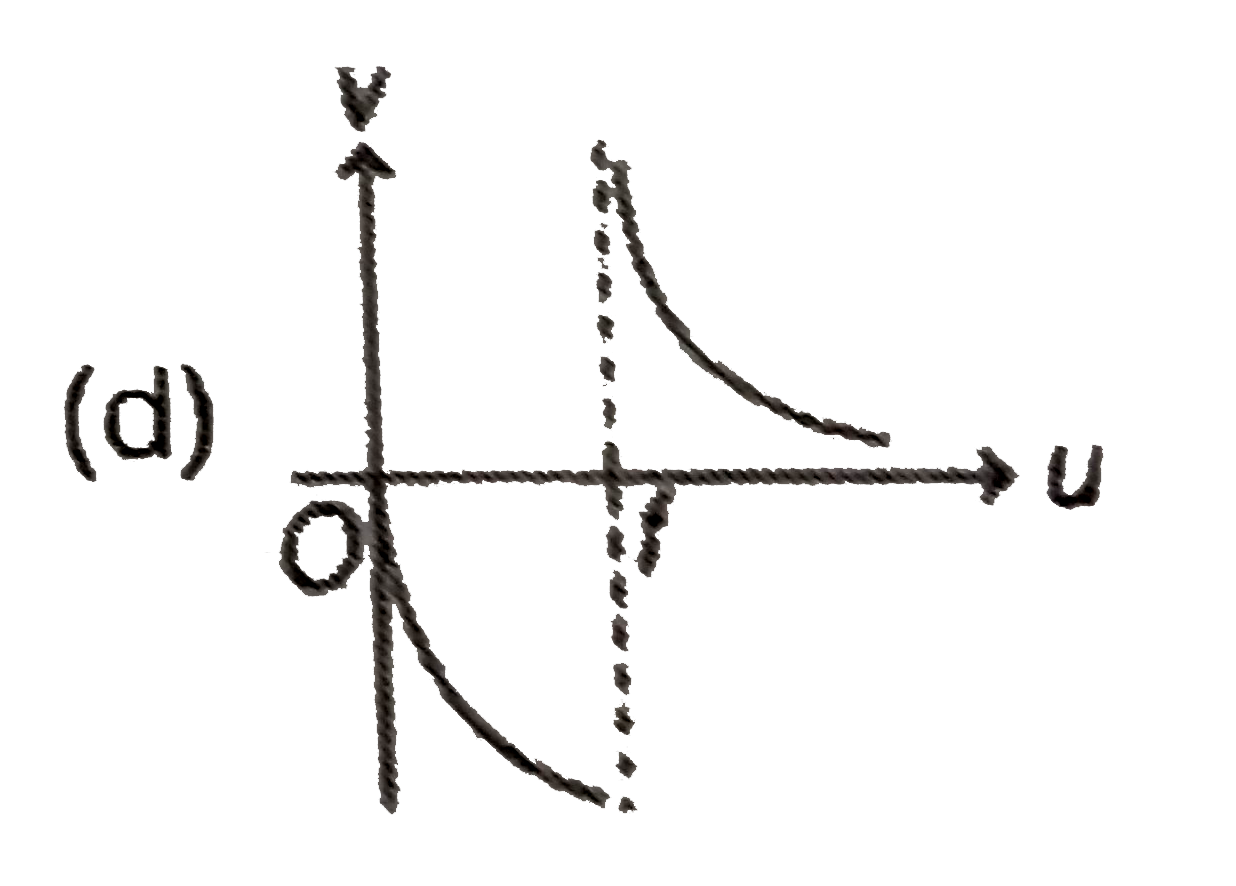
If x , y and z denote the object distance, image distance and the radius of curvature respectively of a spherical mirror, which one of the following is the correct relation between them ?
AZ =2xyx−yBZ=2x+yxyCZ=2xyx−yDZ=2x−yxy
Giving reasons, the 'signs' (positive or negative) which can be given to the following :
(a) object distance
(b) image distances
( c) image distances
(u) for a concave mirror or convex mirror
(v) for a concave mirror (v) for a convex mirror
View Solution(a) State the relation between object distance, image distance and focal length of a spherical mirror.
(b) Draw a ray diagram to show the image formed by a concave mirror when an object is placed between pole and focus of the mirror.
(c ) A concave mirror of focal length 15 cm forms an image of an object kept at a distance of 10 cm from the mirror. Find the position, nature and size of the image formed by it.
View SolutionThe minimum distance between the object and its real image for concave mirror is
View SolutionThe minimum distance between the object and its real image for concave mirror is
View SolutionThe minimum distance between the object and its real image for concave mirror is
View Solution
