A glass sphere (μ =1.5) of radius 20 cm has small air bubble 4 cm below its centre. The sphere is viewed from outside and along vertical line through the bubble. The apparent depth of the bubble below the surface of sphere is (in cm)
13.33
26.67
15
30
The correct Answer is:B
To find the apparent depth of the air bubble below the surface of the glass sphere, we can use the formula that relates the refractive indices and distances in optics. Here’s a step-by-step solution:
Step 1: Identify the parameters
- Refractive index of air, μ2=1
- Refractive index of glass, μ1=1.5
- Radius of the glass sphere, R=20cm
- Depth of the bubble from the center of the sphere, d=4cm
Step 2: Calculate the object distance (U)
The object distance U is measured from the surface of the sphere to the bubble. Since the bubble is 4 cm below the center of the sphere, we need to account for the radius of the sphere:
U=−(R−d)=−(20cm−4cm)=−16cm
Step 3: Use the lens maker's formula
We use the formula for refraction at a spherical surface:
μ2V−μ1U=μ2−μ1R
Substituting in the known values:
1V−1.5−16=1−1.5−20
Step 4: Simplify the equation
Calculating the right side:
1−1.5−20=−0.5−20=0.520=140
Now substituting back into the equation:
1V+1.516=140
Step 5: Find a common denominator
The common denominator for the fractions is 80:
1V+1.5×580=280
This simplifies to:
1V+7.580=280
Step 6: Solve for 1V
Rearranging gives:
1V=280−7.580=−5.580
Step 7: Calculate V
Taking the reciprocal:
V=80−5.5=−805.5≈−14.55cm
Step 8: Calculate the apparent depth
The apparent depth of the bubble is given by the absolute value of V:
Apparent Depth=|V|≈14.55cm
Final Result
The apparent depth of the bubble below the surface of the sphere is approximately 14.55 cm.
---
- Refractive index of air, μ2=1
- Refractive index of glass, μ1=1.5
- Radius of the glass sphere, R=20cm
- Depth of the bubble from the center of the sphere, d=4cm
The object distance U is measured from the surface of the sphere to the bubble. Since the bubble is 4 cm below the center of the sphere, we need to account for the radius of the sphere:
We use the formula for refraction at a spherical surface:
Calculating the right side:
The common denominator for the fractions is 80:
Rearranging gives:
Taking the reciprocal:
The apparent depth of the bubble is given by the absolute value of V:
The apparent depth of the bubble below the surface of the sphere is approximately 14.55 cm.
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRAUMENTS BOOK - NARAYNACHAPTER - RAY OPTICS AND OPTICAL INSTRAUMENTS EXERCISE - EXERCISE-2 (C.W)(REFRACTION THROUGH A PRISM )
8 Videos
- RAY OPTICS AND OPTICAL INSTRAUMENTS BOOK - NARAYNACHAPTER - RAY OPTICS AND OPTICAL INSTRAUMENTS EXERCISE - EXERCISE-2 (C.W)(DISPERSION BY A PRISM )
4 Videos
- RAY OPTICS AND OPTICAL INSTRAUMENTS BOOK - NARAYNACHAPTER - RAY OPTICS AND OPTICAL INSTRAUMENTS EXERCISE - EXERCISE-2 (C.W)(REFRACTION)
20 Videos
- NUCLEI BOOK - NARAYNACHAPTER - NUCLEI EXERCISE - ASSERTION & REASON
5 Videos
- SEMI CONDUCTOR DEVICESBOOK - NARAYNACHAPTER - SEMI CONDUCTOR DEVICESEXERCISE - Level-II (H.W)
36 Videos
Similar Questions
A glass sphere(μ=1.5) with a radius of 15.9 cm has a tiny air bubble 5 cm its centre.This sphere is viewed looking down along the extended radius containing the bubble.What is the apparent depth of the bubble below the sirface of the sphere ?
8.57 cm from top
View SolutionA glass sphere of (μ=1.5) with a radius of 15.0cm has a tiny air bubble 5cm above its centre. The sphere is viewed looking down along the extended radius containing the bubble. What is the apparent depth of the bubble below the surface of the sphere?
View Solution
Knowledge Check
There is a small air bubble inside a glass sphere (μ=1.5) of radius 5 cm. The bubble is 7.5 cm below the surface of the glass. The sphere is placed inside water (μ=43) such that the top surface of glass is 10 cm below the surface of water. The bubble is viewed normally from air. Find the apparent depth on the bubble.
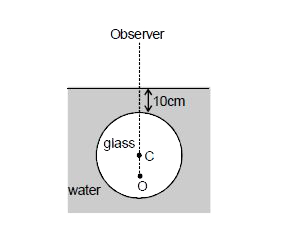 A15 cm below the surface of waterB10.5 cm below the surface of waterC16.66 cm below the surface of waterD13.5 cm below the surface of water
A15 cm below the surface of waterB10.5 cm below the surface of waterC16.66 cm below the surface of waterD13.5 cm below the surface of water
There is a small air bubble inside a glass sphere (μ=1.5) of radius 10 cm. The bubble is 4.0cm below the surface and is viewd normally from the outside. Find the apparent dipth of the bubble.

View SolutionFig shows a small air bubble inside a glass sphere (μ=1.5) of radius 10 cm. the bubble is 4.0 cm below the surface and is viewed normally from the outside. Find the apparent depth of the bubble.
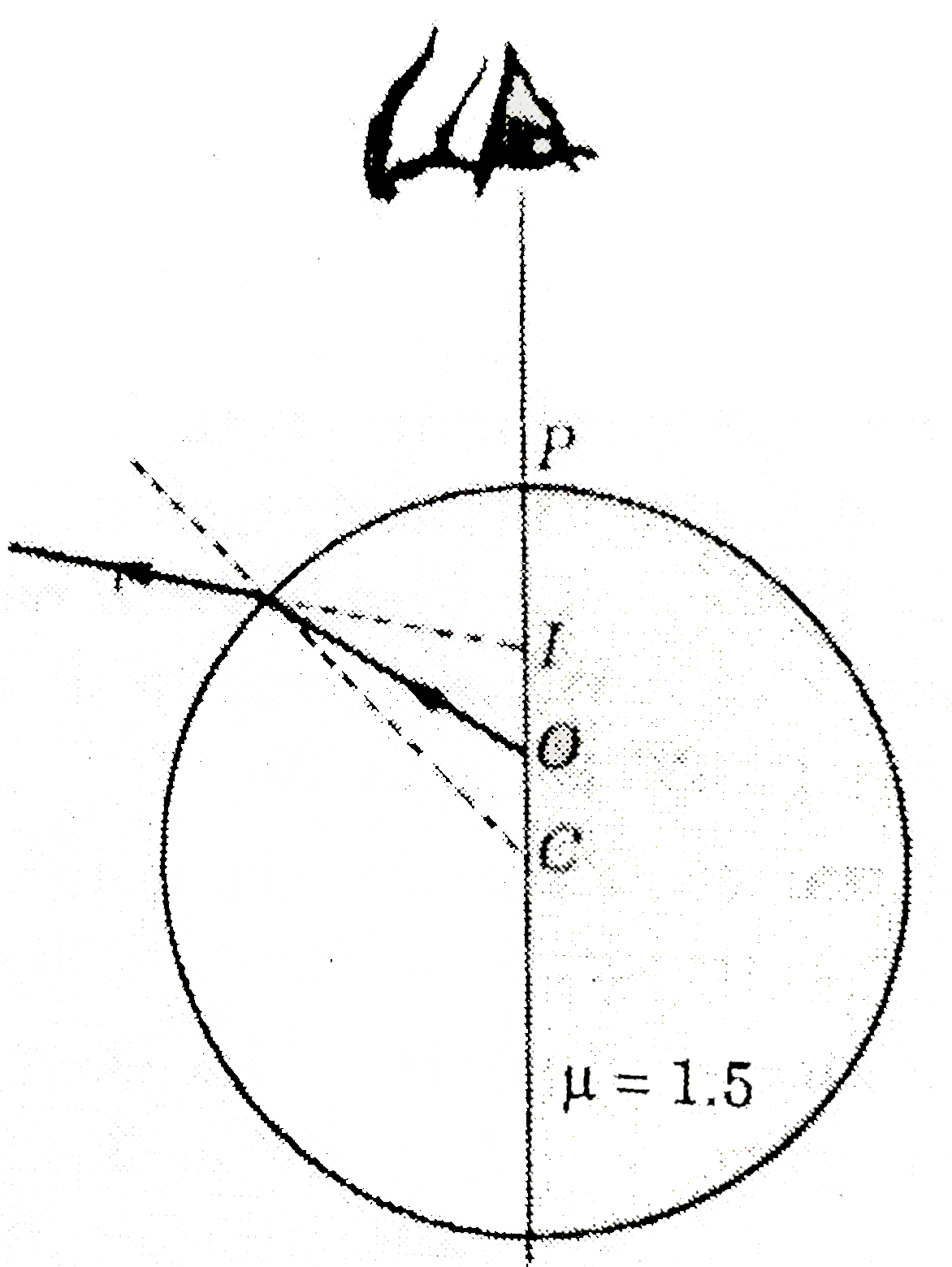
View SolutionThere is a small air bubble inside a glass sphere (μ=1.5) of radius 10 cm. The bubble is 4.0cm below the surface and is viewd normally from the outside. Find the apparent dipth of the bubble.

View SolutionA glass sphere of radius 15 cm has a small bubble 6 cm from its centre. The bubble is viewed along a diameter of the sphere from the side on which it lies. How for from the surface will it appear to be if the refractive index of glass is 1.5 ?
View SolutionThere is small air bubble inside a glass sphere (μ=1.5) of radius 5cm. The bubble is at 'O' at 7.5cm below the surface of the glass. The sphere is placed inside water (μ=43) such that the top surface of glass is 10cm below the surface of water. The bubble is viewed normally from air. Find the apperent depth of the bubble.

View SolutionA glass sphere of radius 5 cm has a small bubble at a distance 2 cm from its centre. The bubble is viewed along a Diameter of the sphere from the side on which it lies.How far from the surface will it appear.Refractive index of glass is 1.5
2.5 cm behind the surface
View SolutionA spherical solid glass paper weight of diameter 6 cm has a small air bubble at a distance of 1.5 cm from the centre. If the air bubble be viewed from the side to which it is nearest along the line joining the bubble and the centre, find where will it appear.
View Solution
