A particle covers 150m in 8th second starting from rest its acceleration is
1) 15ms−2
2) 20ms−2
3) 10ms−2
4) 8ms−2
The correct Answer is:B
To find the acceleration of a particle that covers 150 meters in the 8th second while starting from rest, we can use the formula for the distance covered in the nth second of motion:
Sn=u+a2(2n−1)
Where:
- Sn is the distance covered in the nth second,
- u is the initial velocity,
- a is the acceleration,
- n is the nth second.
1. Identify the given values:
- Distance covered in the 8th second, S8=150m
- Initial velocity, u=0m/s (since the particle starts from rest)
- n=8
2. Substitute the known values into the formula:
S8=u+a2(2n−1)
Substituting the values:
150=0+a2(2⋅8−1)
3. Simplify the equation:
150=a2(16−1)
150=a2⋅15
4. Multiply both sides by 2 to eliminate the fraction:
300=15a
5. Solve for acceleration a:
a=30015
a=20m/s2
Final Answer:
The acceleration of the particle is 20m/s2.
---
- Sn is the distance covered in the nth second,
- u is the initial velocity,
- a is the acceleration,
- n is the nth second.
- Distance covered in the 8th second, S8=150m
- Initial velocity, u=0m/s (since the particle starts from rest)
- n=8
S8=u+a2(2n−1)
Substituting the values:
150=0+a2(2⋅8−1)
150=a2(16−1)
150=a2⋅15
300=15a
a=30015
a=20m/s2
The acceleration of the particle is 20m/s2.
Similar Questions
A particle starting from rest moves in a straight line with acceleration as shown in the a-t graph. Find the distance (in m) travelled by the particle in the first four seconds from start of its motion.
Q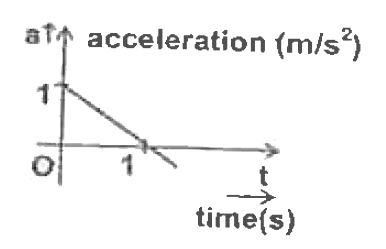
View SolutionA particle moves in a straight line with constant acceleration If it covers 10 m in first second and 20 m in next second find its initial velocity.
View Solution
Knowledge Check
A particle starting from rest. Its acceleration (a) versus time (t) is as shown in the figure.
The maximum speed of the particle will be.
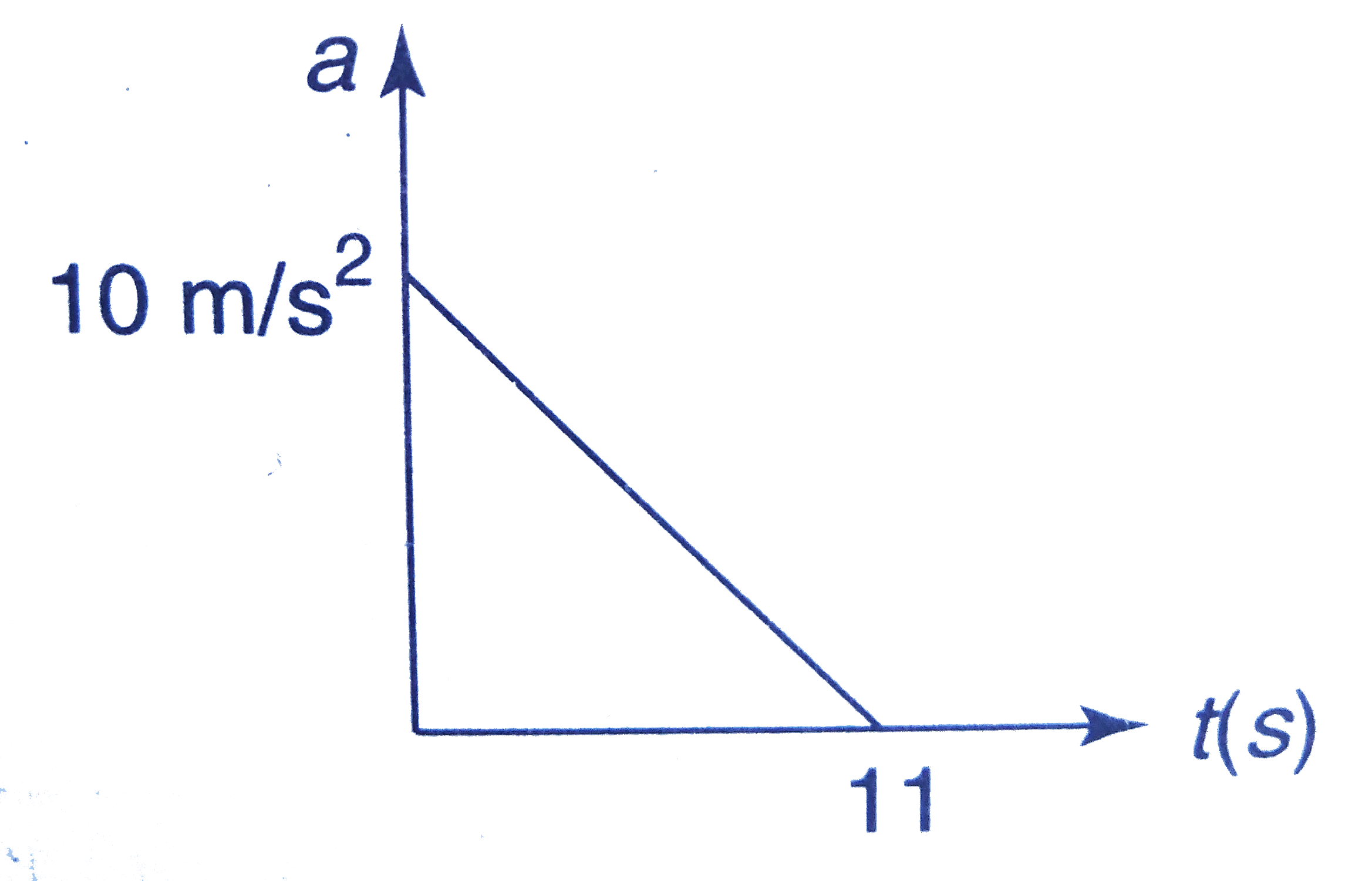 A110m/sB55m/sC550m/sD660m/s
A110m/sB55m/sC550m/sD660m/sA body A starts from rest with an acceleration a1. After 2 seconds, another body B starts from rest with an acceleration a2. If they travel equal distances in the 5th second, after the start of A, then the ratio a1:a2 is equal to :
A5:9B5:7C9:5D9:7A body A starts from rest with an acceleration a1. After 2 seconds, another body B starts from rest with an acceleration a2. If they travel equal distances in the 5th second, after the start of A, then the ratio a1:a2 is equal to :
A5:9B5:7C9:5D9:7
The distance travelled by a particle starting from rest and moving with an acceleration 4/3m/s2 ,in the third-second is
View SolutionA truck starts from rest with an acceleration of 1.5m/s2 car 150 m behind starts from rest with an acceleration of 2m/s2. How long will it take before both the truck and car side byside, and how much distance is traveled by each?
View SolutionA particle starts from rest. Its acceleration is varying with time as shown in the figure. When the particle comes to rest, its distance from its starting point is

View SolutionA particle starts moving from rest in a from rest in a straight line. Its acceleration vs time (a−t) graph is shown in figure. The speed of particle is maximum at.

View SolutionA particle moves with constant acceleration along a straight line streaing from rest. The percentage increase in its displacement during the 4th second compared to that in the 3rd second is
View Solution
