If S1 is surface satellite and S2 is geostationary satellite, with time periods T1 and T2, orbital velocities V1 and V2
T1>T(_(2),V1>V2
T2>T2,V1<V2
T1<T2,V1<V2
T1<T2,V1>V2
The correct Answer is:D
To solve the problem regarding the relationship between the time periods and orbital velocities of a surface satellite (S1) and a geostationary satellite (S2), we can follow these steps:
Step 1: Understand the Definitions
- Surface Satellite (S1): A satellite that orbits very close to the Earth's surface.
- Geostationary Satellite (S2): A satellite that orbits the Earth at a height where it appears to be stationary relative to the Earth's surface, typically at an altitude of about 36,000 km.
Step 2: Determine the Distances from the Center of the Earth
- Let R1 be the distance of the surface satellite from the center of the Earth.
- Let R2 be the distance of the geostationary satellite from the center of the Earth.
- Since the geostationary satellite is much higher, we have R2>R1.
Step 3: Apply Kepler's Third Law
According to Kepler's Third Law, the square of the time period T of a satellite is directly proportional to the cube of the semi-major axis (or radius in circular orbits) of its orbit:
T2∝R3
This implies:
T22T21=R32R31
Since R2>R1, it follows that:
T2>T1
Step 4: Determine the Orbital Velocities
The orbital velocity V of a satellite is given by the formula:
V=√GMR
where G is the gravitational constant and M is the mass of the Earth.
For the surface satellite (S1):
V1=√GMR1
For the geostationary satellite (S2):
V2=√GMR2
Since R2>R1, it follows that:
V2<V1
Step 5: Summarize the Relationships
From the above analysis, we conclude:
- The time period of the geostationary satellite is greater than that of the surface satellite:
T2>T1
- The orbital velocity of the geostationary satellite is less than that of the surface satellite:
V2<V1
Final Answer
Thus, the relationships can be summarized as:
- T1<T2
- V1>V2
- Surface Satellite (S1): A satellite that orbits very close to the Earth's surface.
- Geostationary Satellite (S2): A satellite that orbits the Earth at a height where it appears to be stationary relative to the Earth's surface, typically at an altitude of about 36,000 km.
- Let R1 be the distance of the surface satellite from the center of the Earth.
- Let R2 be the distance of the geostationary satellite from the center of the Earth.
- Since the geostationary satellite is much higher, we have R2>R1.
According to Kepler's Third Law, the square of the time period T of a satellite is directly proportional to the cube of the semi-major axis (or radius in circular orbits) of its orbit:
T2∝R3
This implies:
T22T21=R32R31
Since R2>R1, it follows that:
T2>T1
The orbital velocity V of a satellite is given by the formula:
V=√GMR
where G is the gravitational constant and M is the mass of the Earth.
V1=√GMR1
For the geostationary satellite (S2):
V2=√GMR2
Since R2>R1, it follows that:
V2<V1
From the above analysis, we conclude:
- The time period of the geostationary satellite is greater than that of the surface satellite:
T2>T1
- The orbital velocity of the geostationary satellite is less than that of the surface satellite:
V2<V1
Thus, the relationships can be summarized as:
- T1<T2
- V1>V2
Topper's Solved these Questions
- GRAVITATIONBOOK - NARAYNACHAPTER - GRAVITATIONEXERCISE - LEVEL I(C.W.)
51 Videos
- GRAVITATIONBOOK - NARAYNACHAPTER - GRAVITATIONEXERCISE - LEVEL II (C.W.)
38 Videos
- GRAVITATIONBOOK - NARAYNACHAPTER - GRAVITATIONEXERCISE - EXERCISE -IV
40 Videos
- FRICTIONBOOK - NARAYNACHAPTER - FRICTIONEXERCISE - Passage type of questions I
6 Videos
- KINETIC THEORY OF GASESBOOK - NARAYNACHAPTER - KINETIC THEORY OF GASESEXERCISE - LEVEL-III(C.W)
52 Videos
Similar Questions
Knowledge Check
If ve is escape velocity and v0, is orbital velocity of satellite for orbit close to the earth's surface. Then are related by
Av0=√2veBn0=neCve=v02Dve=√2v0Statement I: If time period of a satellite revolving in circular orbit in equatorial plane is 24h, then it must be a, geostationary satellite.
Statement II: Time period of a geostationary satellite is 24h.AStatement I is True, Statement II is True: Statement II is a correct explanation for Statement I.BStatement I is True, Statement II is True: Statement II is Not a correct explanation for Statement I.CStatement I is True, Statement II is False.DStatement I is False, Statement II is True.Two satellites S1 and S2 are revolving around the earth in coplanar concentric orbits in the opposite sense. At t=0, the position of satellites are shown in the diagram. The periods of S1 and S2 are 4h and 24h, respectively. The radius of orbit of S1 is 1.28×104km. For this situation, mark the correct statement (s).
 AThe angular velocity of S2 as observed by S1 at t=12h is 0.468πrads−1BThe two satellites are closet to each other for the first tme at t=12h and then after every 24h they are closet to each other.CThe orbital velocity of S1 is 0.64π×104km.DThe velocity of S1 relative to S2 is continuously changing in magnitude and direction both.
AThe angular velocity of S2 as observed by S1 at t=12h is 0.468πrads−1BThe two satellites are closet to each other for the first tme at t=12h and then after every 24h they are closet to each other.CThe orbital velocity of S1 is 0.64π×104km.DThe velocity of S1 relative to S2 is continuously changing in magnitude and direction both.
Derive expression for the orbital velocity of a satellite and its time period. What is a geostationary satellite. Obtain the expression for the height of the geostationary satellite.
View SolutionThe area of hole (1) is A1 and of hole (2) is A2. The velocity of efflux and range of liquid is v1,v2andx1,x2 for holes (1) and (2) respectively. The time taken by liquid, jet to reach the ground from holes (1) and (2) are t1andt2 respectively. Cross section of tank is very very large compared to size of holes.
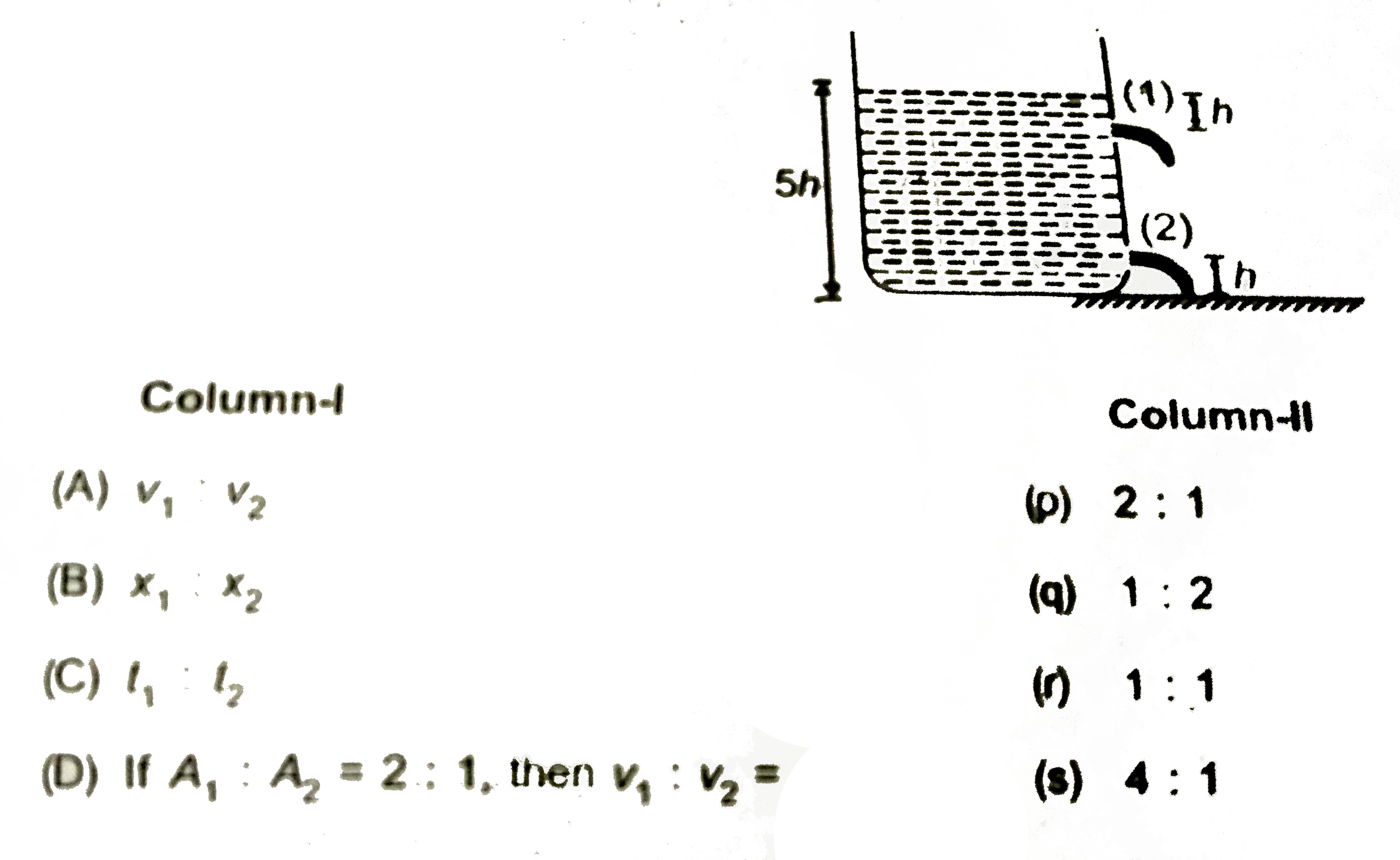
Column-IColumn-II(A)v1:v2(p)2:1(B)x1:x2(q)1:2(C)t1:t2(r)1:1(D)ifA1:A2=2:1,thenv1:v2=(s)4:1
View SolutionOrbital radius of a satellite S of earth is four times that s communication satellite C. Period of revolution of S is :-
View SolutionTwo particles of masses m1 and m2 in projectile motion have velocities →v1 and →v2 , respectively , at time t=0. They collide at time t0. Their velocities become →v'1 and →v'2 at time 2t0 while still moving in air. The value of ∣∣∣(m1→v'1+m2→v'2)−(m1→v1+m2→v2)∣∣∣
View SolutionIf Ve is the escape velocity and V0 is orbital velocity of a satellite for orbit close to the earth's surface. Then these are related by
View Solution
