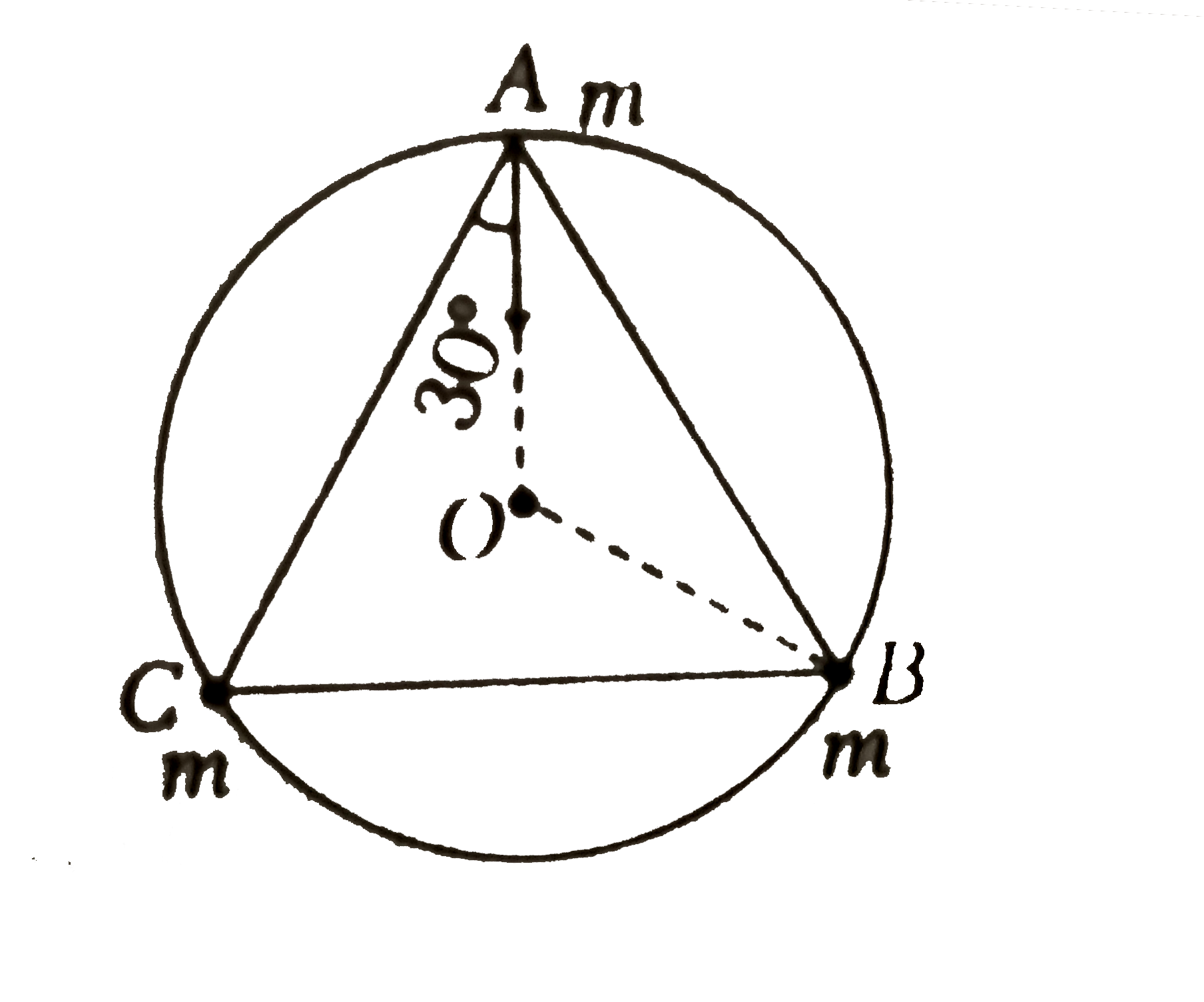
Three identical particles each of mass "m" are arranged at the corners of an equiliteral triangle of side "L". If they are to be in equilibrium, the speed with which they must revolve under the influence of one another's gravity in a circular orbit circumscribing the triangle is

A

$\sqrt{\frac{3 G m}{L}}$

B

$\sqrt{\frac{G m}{L}}$

C

$\sqrt{\frac{G m}{3 L}}$

D

$\sqrt{\frac{3 G m}{L^{2}}}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

$\sqrt{3} F = \frac{m v^{2}}{r}, F = \frac{G m_{1} m_{2}}{L^{2}}$ and $r = \frac{L}{\sqrt{3}}$

|

Updated on:21/07/2023

Class 11 PHYSICS GRAVITATION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Three particle each of mass m are placed at the corners of equilateral triangle of side l

Which of the following is/are correct ?
AMoment of inertia about axis '1' is $\frac{5}{4} m l^{2}$
BMoment of inertia about axis '2' is $\frac{3}{4} m l^{2}$
CMoment of inertia about an axis passing through one corner and perpendicular to the plane is $2 m l^{2}$
DAll of these
Question 2 - Select One
Three particles each of mass $m$ are arranged at the corners of an equililateral triangle of side $L$ . If one of masses is doubled. The shift in the centre of mass of the system
A $\frac{L}{\sqrt{3}}$
B $\frac{L}{4 \sqrt{3}}$
C $\frac{\sqrt{3} L}{4}$
D $\frac{L}{2 \sqrt{3}}$
Question 3 - Select One
Three particle each of mass $m$ , are located at the vertices of an equilateral triangle of side a. At what speed must they move if they all revolve under the influence of their gravitational force of attraction in a circular orbit circumscribing the triangle while still preserving the equilateral triangle ?

A $\sqrt{\frac{G m}{a}}$
B $\sqrt{\frac{2 G m}{a}}$
C $\sqrt{\frac{3 G m}{a}}$
D $\sqrt{\frac{4 G m}{a}}$

NARAYNA-GRAVITATION-EXERCISE -II (C.W.)

Home
Ask Doubt
Profile