Two particle of masses m and 2m are at a distance 3r apart at the ends of a straight line AB. C is the centre of mass of the system. The magnitude of the gravitational force on a unit mass placed at C due to the masses is
zero
7Gm4r2
9Gm4r2
3Gm2r2
The correct Answer is:B
F=Gm1m2R2,Fnet=F2−F1
Topper's Solved these Questions
- GRAVITATIONBOOK - NARAYNACHAPTER - GRAVITATIONEXERCISE - EXERCISE -III
42 Videos
- GRAVITATIONBOOK - NARAYNACHAPTER - GRAVITATIONEXERCISE - EXERCISE -IV
40 Videos
- GRAVITATIONBOOK - NARAYNACHAPTER - GRAVITATIONEXERCISE - EXERCISE -II (C.W.)
38 Videos
- FRICTIONBOOK - NARAYNACHAPTER - FRICTIONEXERCISE - Passage type of questions I
6 Videos
- KINETIC THEORY OF GASESBOOK - NARAYNACHAPTER - KINETIC THEORY OF GASESEXERCISE - LEVEL-III(C.W)
52 Videos
Similar Questions
Four particles of masses m, m, 2m and 2m are placed at the four corners of square of side a. Find the centre of mass of the system.
View SolutionA solid sphere of mass m and radius r is placed inside a hollow thin spherical shell of mass M and radius R as shown in figure−6.30. A particle of mass m' is placed on the line joining the two centres at a distance x from the point of contact of the sphere and the shell. Find the magnitude of the resultant gravitational force on this - particle due to the sphere and the shell if (a) r<x<2r,(b)2r<x<2Rand(c)x>2R.
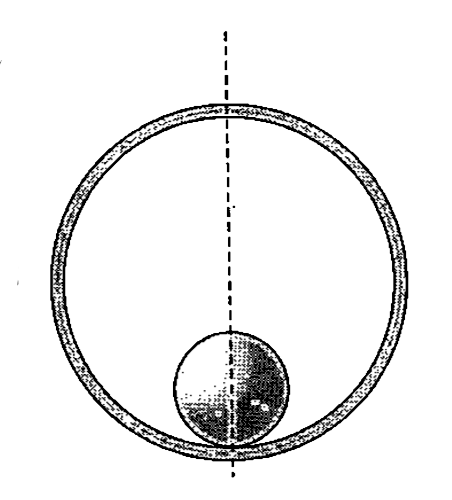
View Solution
Knowledge Check
A solid sphere of mass m radius r is placed inside a hollow thin spherical shell of mass M and radius 2r as shown in figure. A particle of mass m' is placed on the line joining the two centres at a distance x from the point of contact of the sphere and the shell. find the magnitude of the resultant gravitational force on this particle due to the sphere and the shell if
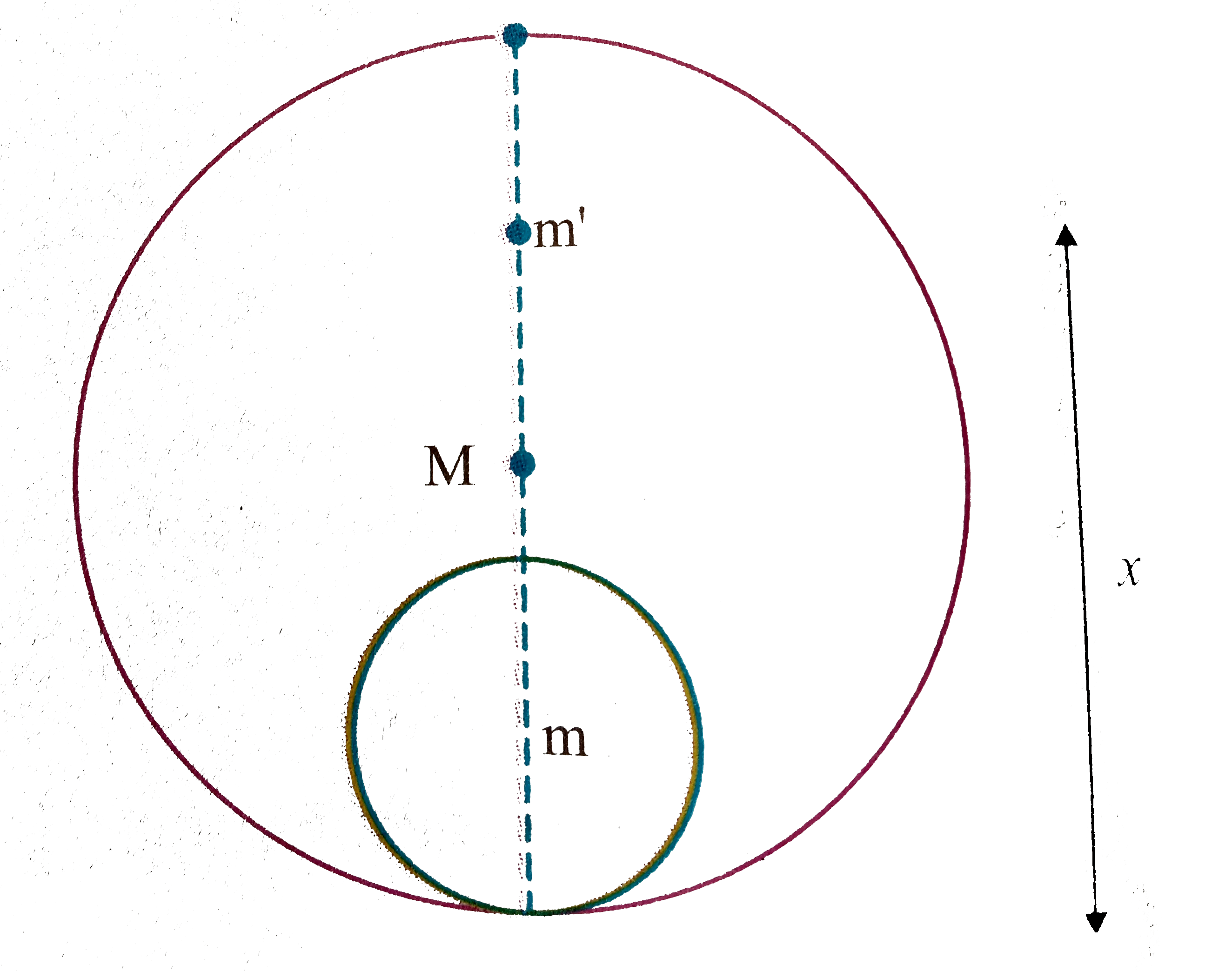
2r<x<2RAGmm'4(x−r)2BGmm'(x−r)2CGmm'(x−r)3D2Gmm'(x−r)2A solid sphere of mass m radius r is placed inside a hollow thin spherical shell of mass M and radius 2r as shown in figure. A particle of mass m' is placed on the line joining the two centres at a distance x from the point of contact of the sphere and the shell. find the magnitude of the resultant gravitational force on this particle due to the sphere and the shell if

x>2RA2GMm'(x−r)2+Gmm'(x+r)2BGMm'2(x−R)2+2Gmm'(x−r)2CGMm'2(x−r)2+2GMm'(x+r)2DGMm'(x−R)2+Gmm'(x−r)2A solid sphere of mass m and radius r is placed inside a hollow thin spherical shell of mass M and radius R as shown in the figure. A particle of mass m' is placed on the line joining the two centres at a distance x from the point of contact of the sphere and the shell. Find the magnitude of the resultant gravitational force on this particle due to the sphere and the shell if

r<x<2rAGmm'(2r−x)2r3BGmm'(x−r)2r3CGmm'(x−r)r3DGmm'(2x−r)r3
Two point masses m and M are separated by a distance L . The distance of the centre of mass of the system from m is
View SolutionTwo point masses m and M are separated bya distance L . The distance of the centre of mass of the system from m is
View SolutionTwo stars of mass m1 and m2 are parts of a binary star system. The radii of their orbits are r1 and r2 respectivey, measured from the centre of mass of the system. The magnitude of gravitational force m1 exerts on m2 is
View SolutionTwo bodies of masses m1 and m2 are separated by a distance R. The distance of the centre of mass of the bodies from the mass m1 is
View SolutionTwo bodies of masses m1 and m2 are separated by a distance R. The distance of the centre of mass of the bodies from the mass m1 is
View Solution
