Find the time period in each of the following cases, if the mass is pulled and left.
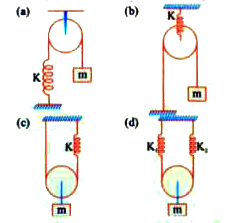
If the mass is pulled down by y and released.
(a)

(b) Here if the mass is pulled down by .y.. The spring will be stretched by y/2.
it will give a force of ky/2,
which gets distributed in each string
br>
(c) Here, if the the mass is pulled through .y.. the spring gets stretched by 2y.
it gives a force 2Ky
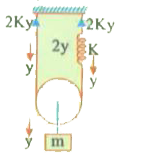
Restoring tension in string connected to the mass .m. is 4 Ky
(d)
now
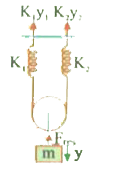
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - EVALUATE YOURSELF - 17videos
OSCILLATIONS
- BOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - EVALUATE YOURSELF - 24videos
OSCILLATIONS
- BOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - DAMPED OSCILLATIONS1videos
OSCILLATIONS
- BOOK - NARAYNACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - PASSAGE TYPE QUESTION6videos
NEWTONS LAWS OF MOTION
- BOOK - NARAYNACHAPTER - PHYSICAL WORLDEXERCISE - C.U.Q10videos
PHYSICAL WORLD
Similar Questions
Knowledge Check
- Question 1 - Select One
Find the time period of SHM of the block of mass M
 AT=2π√M2KBT=2π√MKCT=2π√2MKDT=2π√M4K
AT=2π√M2KBT=2π√MKCT=2π√2MKDT=2π√M4K - Question 2 - Select One
Find the time period of oscillation of block of mass m. Spring, and pulley are ideal. Spring constant is k.
 A2π√mkBπ√mkC4π√mkD2π√m2k
A2π√mkBπ√mkC4π√mkD2π√m2k - Question 3 - Select One
The time period of small oscillations of mass m :-
_S01_040_Q01.png) A2π√m6kB2π√11m6KC2π√6m11KD2π√mK
A2π√m6kB2π√11m6KC2π√6m11KD2π√mK
Find the time period of the oscillation of mass m in figure a,b,c what is the equivalent spring constant of the pair oif springs in each case?
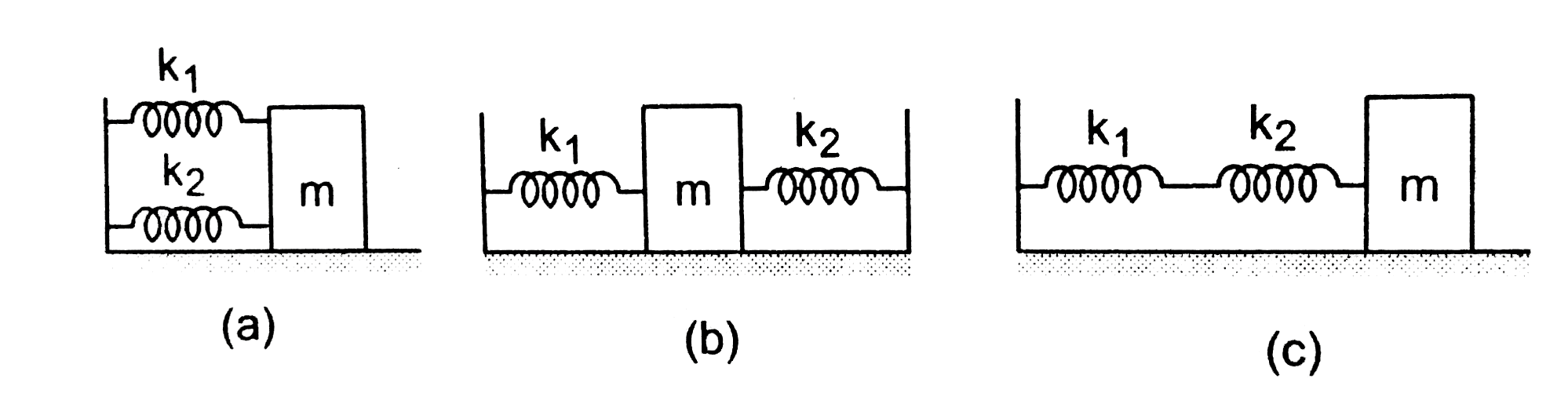 View Solution
View SolutionFind time period of oscillation of the system.
 View Solution
View SolutionThree spring mass systems are shown in figure. Assuming gravity free spece, find the time period of oscillations in each case. What should be the answer if space is not gravity free ?
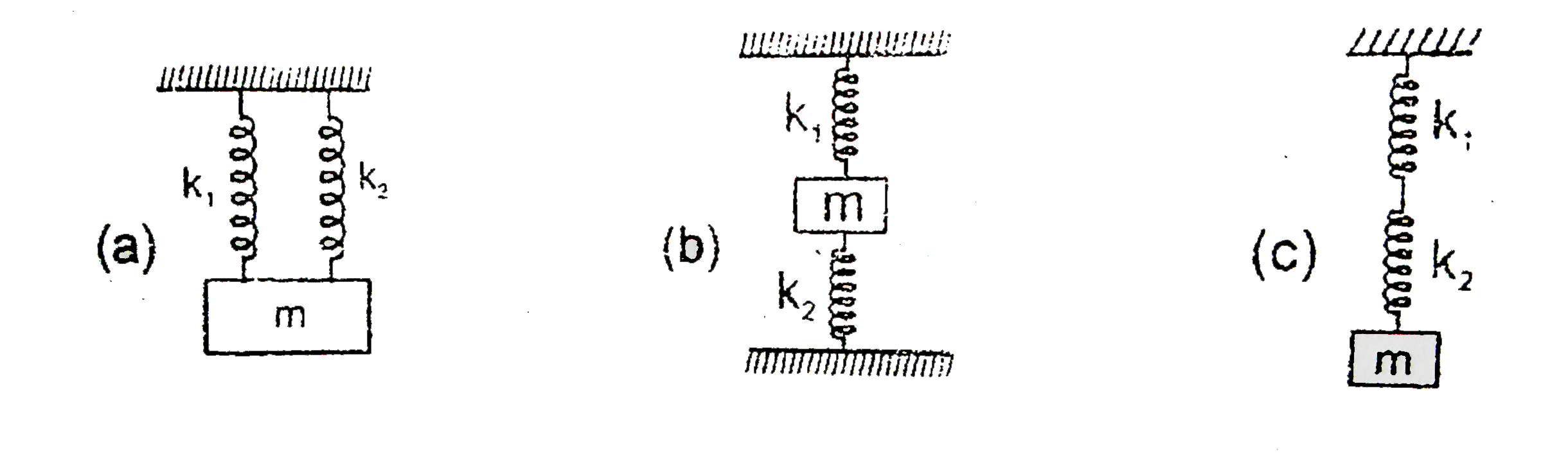 View Solution
View SolutionThree spring mass systems are shown in figure. Assuming gravity free spece, find the time period of oscillations in each case. What should be the answer if space is not gravity free ?
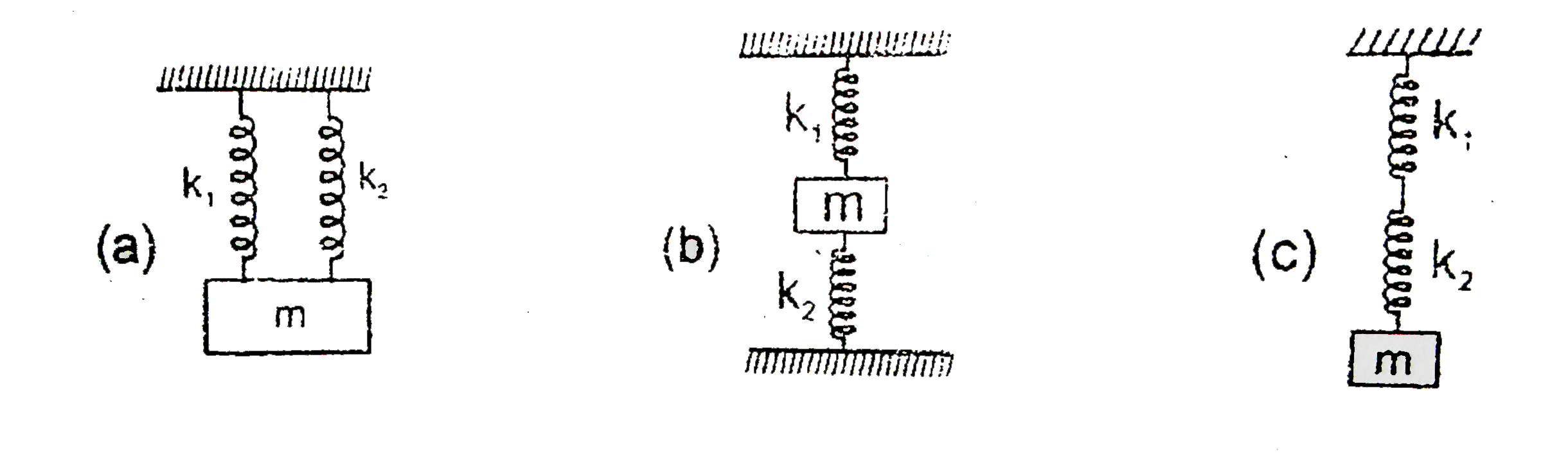 View Solution
View SolutionA spring-block system is executing SHM. The mass of the block is M and the time period of oscillation is T. If the mass of the block is increased by m, then time period becomes 7T4. Now, find the ratio of mM ,
View Solution


