The total mechanical energy of a harmonic oscillator of amplitude 1m and force constant 200N/m is 150J. Then
The minimum PE is zero
The maximum PE is 100 J
The minimum PE is 50 J
The maximum PE is 50 J
The correct Answer is:C
Kmax=12A2=12(200)(1)2=100J
Umin=E−Kmax=50J
Kmin=0⇒Umax=E−Kmin=150−0=150J
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - EXERCISE - II (C.W)27videos
OSCILLATIONS
- BOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - EXERCISE - II (H.W)19videos
OSCILLATIONS
- BOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - EXERCISE - I (C.W)63videos
OSCILLATIONS
- BOOK - NARAYNACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - PASSAGE TYPE QUESTION6videos
NEWTONS LAWS OF MOTION
- BOOK - NARAYNACHAPTER - PHYSICAL WORLDEXERCISE - C.U.Q10videos
PHYSICAL WORLD
Similar Questions
Knowledge Check
- Question 1 - Select One
The total mechanical energy of a hamronic oscillator of amplitude 1m and force constant 200N/m is 150J. Then
AThe minimum PE is ZeroBThe maximum PE is 100JCThe minimum PE is 50JDThe maximum PE is 50J - Question 2 - Select One
The total mechanical energy of a particle performing S.H.M. is 150 J with amplitude 1 m and force constant 200 N/m. Then minimum P.E. is,
A50 JB100 JC150 JDzero - Question 3 - Select One
A linear harmonic oscillator of force constant 106N/m and amplitude 2 cm has
Aa maximum P.E. of 100 JouleBa maximum K.E. of 150 JuleCa total energy of 200 JDa total energy of 300 J
The potential energy of a simple harmonic oscillator of mass 2 kg in its mean position is 5 J. If its total energy is 9 J and its amplitude is 0.01 m, its time period would be
View SolutionThe potential energy of a harmonic oscillator of mass 2 kg in its mean positioin is 5J. If its total energy is 9J and its amplitude is 0.01m, its period will be
View SolutionThe potential energy of a particle of mass m free to move along the x-axis is given by U=(1/2)kx2 for x<0 and U=0 for x≥0 (x denotes the x-coordinate of the particle and k is a positive constant). If the total mechanical energy of the particle is E, then its speed at x=−√2E/k is
View SolutionThe variation of potential energy (U) of a simple harmonic oscillator is as shown. Then force constant of the system is (PE is in joules, displacement 'x' is in mm)
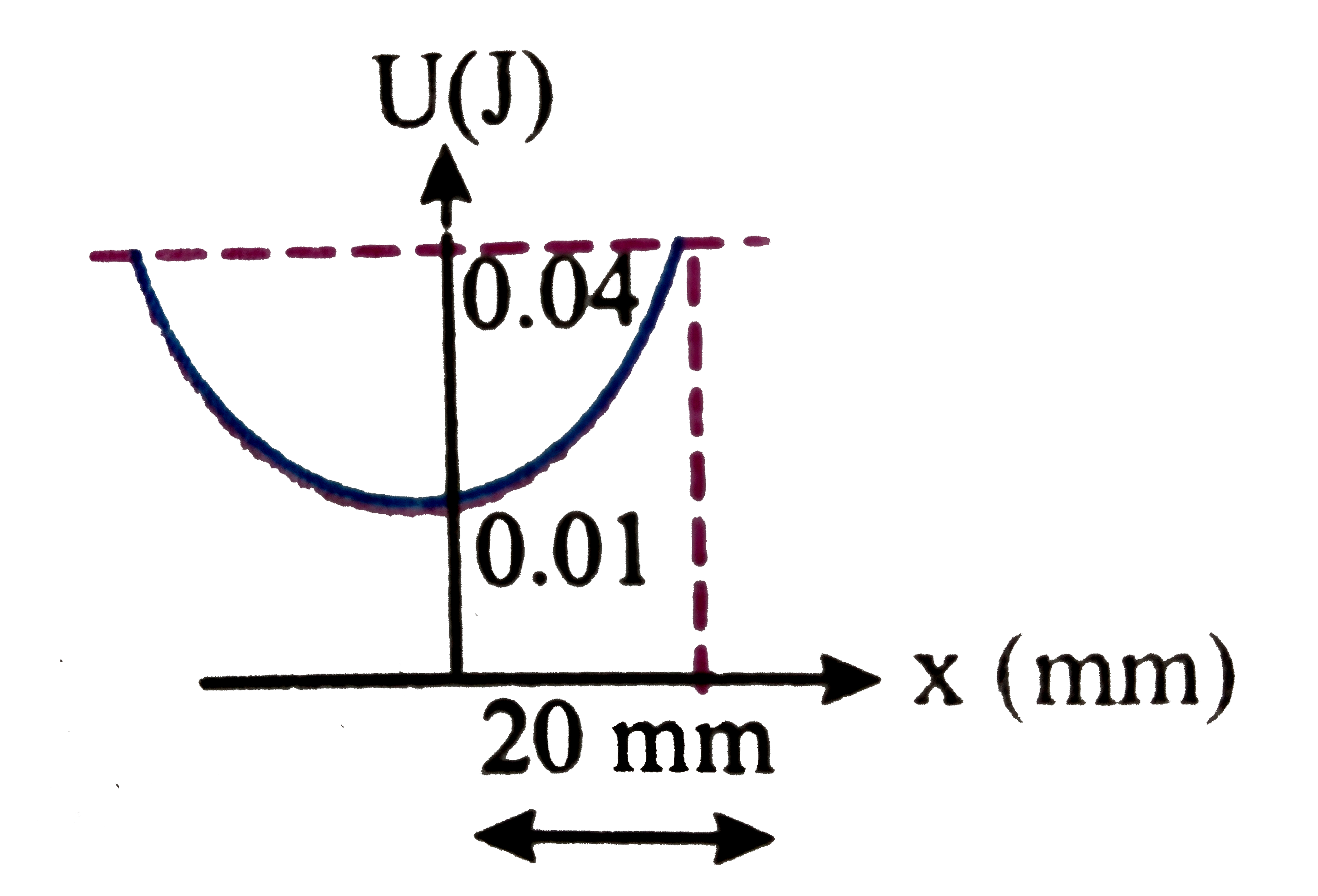 View Solution
View SolutionThe total energy of a harmonic oscillator of mass 2 kg is 9 J. If its potential energy at mean position is 5 J , its KE at the mean position will be
View Solution
