An electron in C5+ ion during the transition from n=3 to n=1 emits light of wavelength
2.85nm
3.6nm
8.7nm
9.8nm
The correct Answer is:A
To find the wavelength of light emitted during the transition of an electron in the C5+ ion from n=3 to n=1, we can follow these steps:
Step 1: Determine the Energy of the Transition
The energy of the transition can be calculated using the formula:
E=13.6Z2(1n21−1n22)
where:
- Z is the atomic number of carbon, which is 6.
- n1=1 (final state)
- n2=3 (initial state)
Step 2: Substitute Values into the Energy Formula
Substituting the values into the formula:
E=13.6×62(112−132)
Calculating Z2:
Z2=62=36
Now, calculate the fractions:
112−132=1−19=99−19=89
Now substituting back:
E=13.6×36×89
Step 3: Calculate the Energy
Calculating E:
E=13.6×36×89=13.6×4×8=13.6×32=435.2eV
Step 4: Convert Energy to Joules
To convert electron volts to joules, use the conversion factor 1eV=1.6×10−19J:
E=435.2eV×1.6×10−19J/eV=6.9632×10−17J
Step 5: Use the Energy to Find Wavelength
Using the formula E=hcλ, where:
- h=6.626×10−34J s (Planck's constant)
- c=3×108m/s (speed of light)
Rearranging for λ:
λ=hcE
Step 6: Substitute Values to Calculate Wavelength
Substituting the values:
λ=(6.626×10−34J s)×(3×108m/s)6.9632×10−17J
Calculating λ:
λ=1.9878×10−256.9632×10−17≈2.85×10−9m
Step 7: Convert Wavelength to Nanometers
To convert meters to nanometers:
λ=2.85×10−9m=2.85nm
Final Answer
The wavelength of light emitted during the transition from n=3 to n=1 in the C5+ ion is approximately 2.85nm.
---
The energy of the transition can be calculated using the formula:
E=13.6Z2(1n21−1n22)
where:
- Z is the atomic number of carbon, which is 6.
- n1=1 (final state)
- n2=3 (initial state)
Substituting the values into the formula:
E=13.6×62(112−132)
Calculating Z2:
Z2=62=36
Now, calculate the fractions:
112−132=1−19=99−19=89
Now substituting back:
E=13.6×36×89
Calculating E:
E=13.6×36×89=13.6×4×8=13.6×32=435.2eV
To convert electron volts to joules, use the conversion factor 1eV=1.6×10−19J:
E=435.2eV×1.6×10−19J/eV=6.9632×10−17J
Using the formula E=hcλ, where:
- h=6.626×10−34J s (Planck's constant)
- c=3×108m/s (speed of light)
λ=hcE
Substituting the values:
λ=(6.626×10−34J s)×(3×108m/s)6.9632×10−17J
Calculating λ:
λ=1.9878×10−256.9632×10−17≈2.85×10−9m
To convert meters to nanometers:
λ=2.85×10−9m=2.85nm
The wavelength of light emitted during the transition from n=3 to n=1 in the C5+ ion is approximately 2.85nm.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
The transition of electron from n = 3 to n = 1 in H atom produces
AEmission spectrumBAbsorption spectrumCPaschen lineDPfund line. - Question 2 - Select One
The electronic transition from n = 2 to n = 1 will produce shortest wave length in (where n = principle quantum state)
ALi2+BHe+CHDH+ - Question 3 - Select One
A photon of energy 10.2 eV corresponds to light of wavelength λ0. Due to an electron transition from n=2 to n=1 in a hydrogen atom, light of wavelength λ is emitted. If we take into account the recoil of the atom when the photon is emitted.
Aλ=λ0Bλ<λ0Cλ>λ0Dthe data is not sufficient to reach a conclusion
In a set of experiment on a hydrogen on a hypothetical one-electron atom, the wavelength of the photons emitted from transition ending in the ground state (n=1) are shown in the energy level diagram
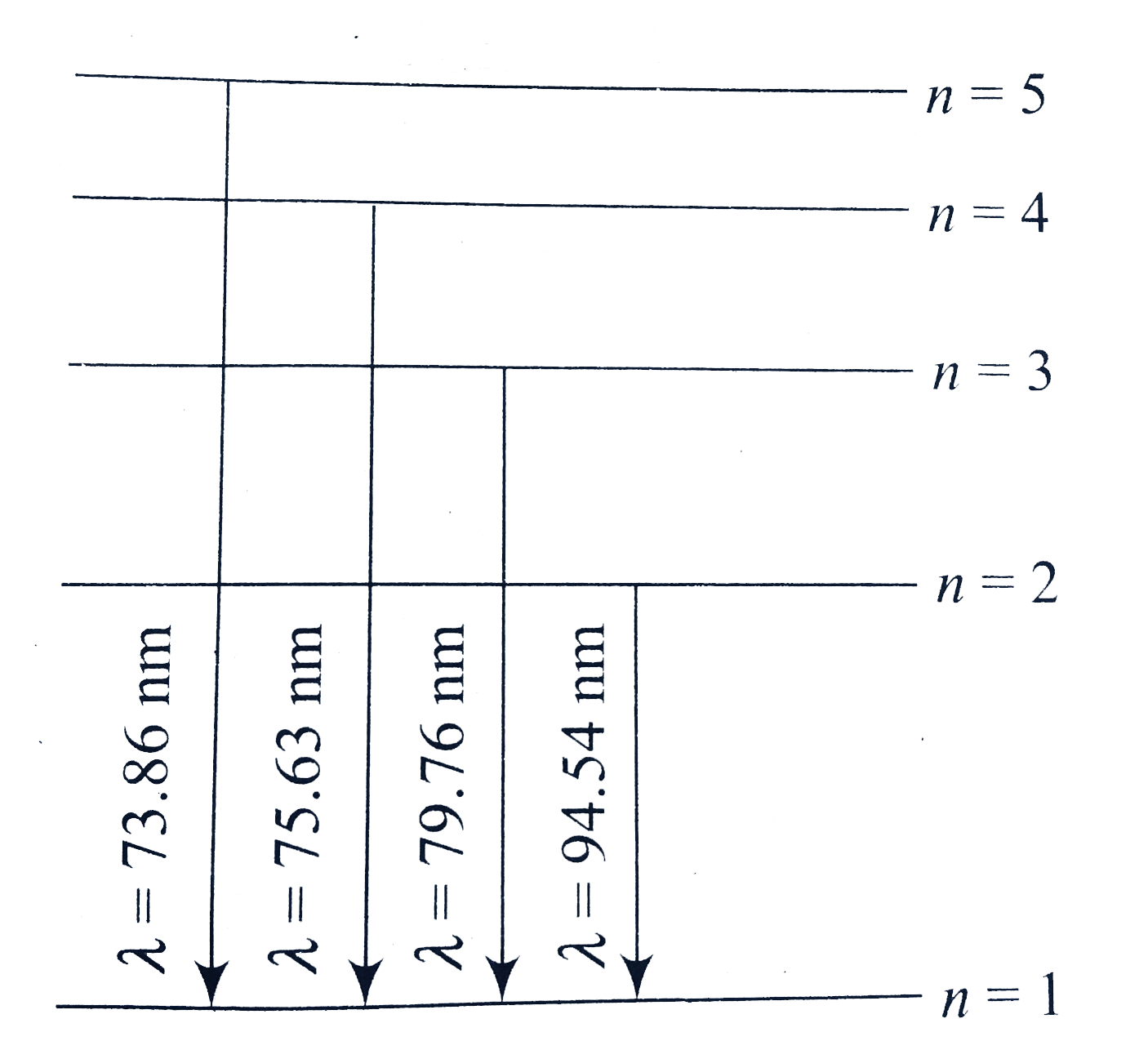
λ5→1=73.86nm
λ4→1=75.63nm
λ3→1=79.76nm
λ2→1=94.54nm
If an electron made a transition from n = 4 to n = 2 level, the wavelength of the light that it would emit is nearlyView SolutionThere is transition from n=1 to n=2 and then n=2 to n=3, then
View SolutionThe ground state energy of an atom is −13.6eV. The photon emitted during the transition of electron from n=3 to n=1 state, is incidenet on a photosensitive material of unknown work function. The photoelectrons are emitted from the materials with a maximum kinetic energy of 9 eV. the threshold wavelength of the material used is
View SolutionIf an electron undergoes transition from n = 2 to n =1 in Li2+ ion , the energy of photon radiated will be best given by
View SolutionWhen an electron do transition from n = 4 to n = 2, then emitted line in spectrum will be:
View Solution

