A conductor with a cavity is charged positively and its surface charge density is σ. If E and V represent the electric field and potential, then inside the cavity
E = 0 and V = 0
E = 0 and σ- constant
V = 0 and σ = constant
E = 0 and V = constant
The correct Answer is:D
To solve the problem regarding the electric field (E) and potential (V) inside a cavity of a positively charged conductor with surface charge density σ, we can follow these steps:
Step 1: Understand the properties of conductors
In electrostatics, the electric field inside a conductor in electrostatic equilibrium is zero. This is due to the fact that charges redistribute themselves on the surface of the conductor until the electric field within the conductor cancels out.
Hint: Remember that in electrostatic equilibrium, the electric field inside a conductor is always zero.
Step 2: Analyze the cavity inside the conductor
Since the conductor has a cavity, we need to consider the implications of having a cavity within a conductor. The charges on the surface of the conductor will redistribute themselves in such a way that the electric field inside the cavity is also zero. This is because any electric field would cause charges to move, contradicting the condition of electrostatic equilibrium.
Hint: Think about how charges behave in response to electric fields and how they distribute themselves on the surface of conductors.
Step 3: Determine the electric field (E) inside the cavity
Since the electric field inside the cavity is zero, we can conclude:
E=0
Hint: Recall that if the electric field is zero, it means that there are no forces acting on any test charge placed inside the cavity.
Step 4: Determine the electric potential (V) inside the cavity
The electric potential inside the cavity will be constant. This is because the electric field is zero, and thus there is no change in potential within the cavity. The potential inside the cavity will be equal to the potential at the surface of the conductor.
Hint: Remember that the potential difference is related to the electric field; if the electric field is zero, the potential does not change.
Step 5: Conclusion
From the analysis, we can summarize:
- The electric field inside the cavity is zero: E=0
- The electric potential inside the cavity is constant: V=V0 (where V0 is the potential at the surface of the conductor).
Thus, the correct answer is that inside the cavity, the electric field is zero, and the potential is constant.
Final Answer:
- E=0
- V=constant
In electrostatics, the electric field inside a conductor in electrostatic equilibrium is zero. This is due to the fact that charges redistribute themselves on the surface of the conductor until the electric field within the conductor cancels out.
Since the conductor has a cavity, we need to consider the implications of having a cavity within a conductor. The charges on the surface of the conductor will redistribute themselves in such a way that the electric field inside the cavity is also zero. This is because any electric field would cause charges to move, contradicting the condition of electrostatic equilibrium.
Since the electric field inside the cavity is zero, we can conclude:
E=0
The electric potential inside the cavity will be constant. This is because the electric field is zero, and thus there is no change in potential within the cavity. The potential inside the cavity will be equal to the potential at the surface of the conductor.
From the analysis, we can summarize:
- The electric field inside the cavity is zero: E=0
- The electric potential inside the cavity is constant: V=V0 (where V0 is the potential at the surface of the conductor).
- E=0
- V=constant
Topper's Solved these Questions
Similar Questions
A spherical conducting shell of inner radius r1 and outer radius r2 has a charge Q.
A charge q is placed at the centre of the shell. Find out the surface charge density on the inner and outer surface of the shell.
Is the electric field inside a cavity (with no charge ) zero. Independent of the fact wheather the shell is spherical or not ? Explain.
View SolutionWhy is electric field intensity inside a charged conductor zero ?
View Solution
Knowledge Check
A nonconducting sphere with a cavity has volume charge density ρ. O1andO2 represent the two centers as shown. The electric fields inside the cavity is E0. Now, an equal and opposite charge is given uniformly to the sphere on its outer surface. The magnitude of electric field inside the cavity becomes
 AzeroBE0C2E0D3E0
AzeroBE0C2E0D3E0The electric intensity at a point near a charged conductor of surface charge density σ is
AE=σ/∈0kBE=σ∈0kCE=σ/2∈0kDE=σ2A spherical charged conductor has surface charge density σ.The intensity of electric field and potential on its surface are E and V .Now radius of sphere is halved keeping the charge density as constant .The new electric field on the surface and potneial at the centre of the sphere are
A4E,VBE,V/2CE,VD2E,4V
A solid sphere of radius 'R' has a cavity of radius R2. The solid part has a uniform charge density 'ρ' and cavity has no charge. Find the electric potential at point 'A'. Also find the electric field (only magnitude) at point 'C' inside the cavity
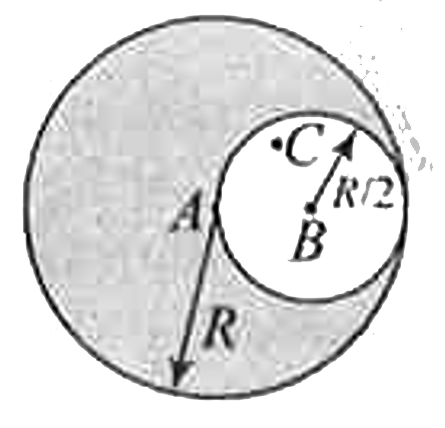
View SolutionFigure shown a charged conductor resting on an insulating stand. If at the point P the charge density is σ, the potential is V and the electric field strength is E, what are the values of these quantities at point Q ?

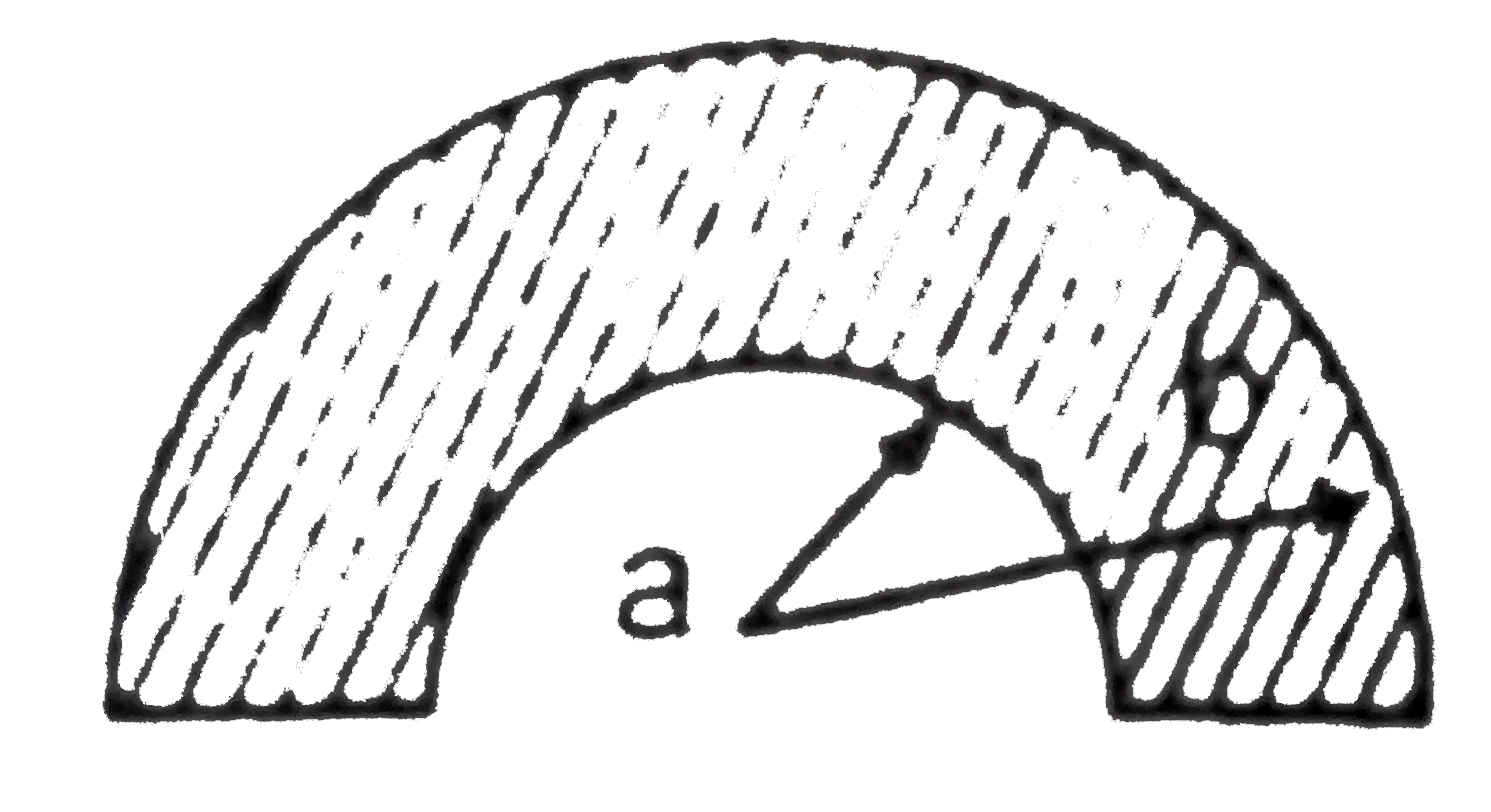
View SolutionA non-conducting semi circular disc (as shown in figure) has a uniform surface charge density σ. The ratio of electric field to electric potential at the centre of the disc will be
View SolutionThe electric intensity at a pont near a charged conductor having a charge density σ is
View SolutionThe electric field inside a spherical shell of uniform surface charge density is
View Solution
