The emf of a cell is 6 V and internal resistance is 0.5kΩ The reading of a Voltmeter having an internal resistance of 2.5kΩ is
6 V
10 V
5 V
0.5 V
The correct Answer is:C
To find the reading of the voltmeter connected across the terminals of a cell with an EMF of 6 V and an internal resistance of 0.5 kΩ, while the voltmeter has an internal resistance of 2.5 kΩ, we can follow these steps:
Step 1: Understand the Circuit Configuration
The cell has an EMF (E) of 6 V and an internal resistance (r) of 0.5 kΩ. The voltmeter, which has an internal resistance (R_v) of 2.5 kΩ, is connected in parallel with the internal resistance of the cell.
Step 2: Calculate the Total Resistance in the Circuit
The total resistance (R_total) seen by the cell can be calculated by adding the internal resistance of the cell and the resistance of the voltmeter in parallel:
1Rtotal=1r+1Rv
Substituting the values:
1Rtotal=10.5kΩ+12.5kΩ
Converting kΩ to Ω:
1Rtotal=1500Ω+12500Ω
Finding a common denominator (2500):
1Rtotal=52500+12500=62500
Thus,
Rtotal=25006≈416.67Ω
Step 3: Calculate the Current in the Circuit
Using Ohm's law, we can find the current (I) flowing through the circuit:
I=ERtotal
Substituting the values:
I=6V416.67Ω≈0.0144A=14.4mA
Step 4: Calculate the Voltage Across the Voltmeter
The voltage across the voltmeter (V_v) can be calculated using Ohm's law:
Vv=I×Rv
Substituting the values:
Vv=14.4mA×2.5kΩ=14.4×2.5V=36V
However, this voltage is not correct as we need to consider the voltage drop across the internal resistance of the cell.
Step 5: Calculate the Voltage Drop Across the Internal Resistance
The voltage drop (V_drop) across the internal resistance of the cell can be calculated as:
Vdrop=I×r
Substituting the values:
Vdrop=14.4mA×0.5kΩ=14.4×0.5V=7.2V
Step 6: Calculate the Reading of the Voltmeter
Now, the reading of the voltmeter can be calculated as:
Vreading=E−Vdrop
Substituting the values:
Vreading=6V−7.2V=−1.2V
This indicates that the voltmeter reading is not possible under these conditions.
Final Step: Correct Calculation
Revisiting the calculation, we realize that the voltage across the voltmeter is given by:
Vv=I×Rv=14.4mA×2.5kΩ=36V
Thus, the reading of the voltmeter is:
Vv=6V×2.5kΩ(0.5kΩ+2.5kΩ)=15V3kΩ=5V
Conclusion
The reading of the voltmeter is 5 V.
The cell has an EMF (E) of 6 V and an internal resistance (r) of 0.5 kΩ. The voltmeter, which has an internal resistance (R_v) of 2.5 kΩ, is connected in parallel with the internal resistance of the cell.
The total resistance (R_total) seen by the cell can be calculated by adding the internal resistance of the cell and the resistance of the voltmeter in parallel:
Using Ohm's law, we can find the current (I) flowing through the circuit:
The voltage across the voltmeter (V_v) can be calculated using Ohm's law:
The voltage drop (V_drop) across the internal resistance of the cell can be calculated as:
Now, the reading of the voltmeter can be calculated as:
Revisiting the calculation, we realize that the voltage across the voltmeter is given by:
The reading of the voltmeter is 5 V.
Topper's Solved these Questions
Similar Questions
Knowledge Check
In figure, the e.m.f. of the cell is 120V and internal resistance is negligible. The resistance of the voltmeter is 80 ohm. The % error in reading of voltmeter will be
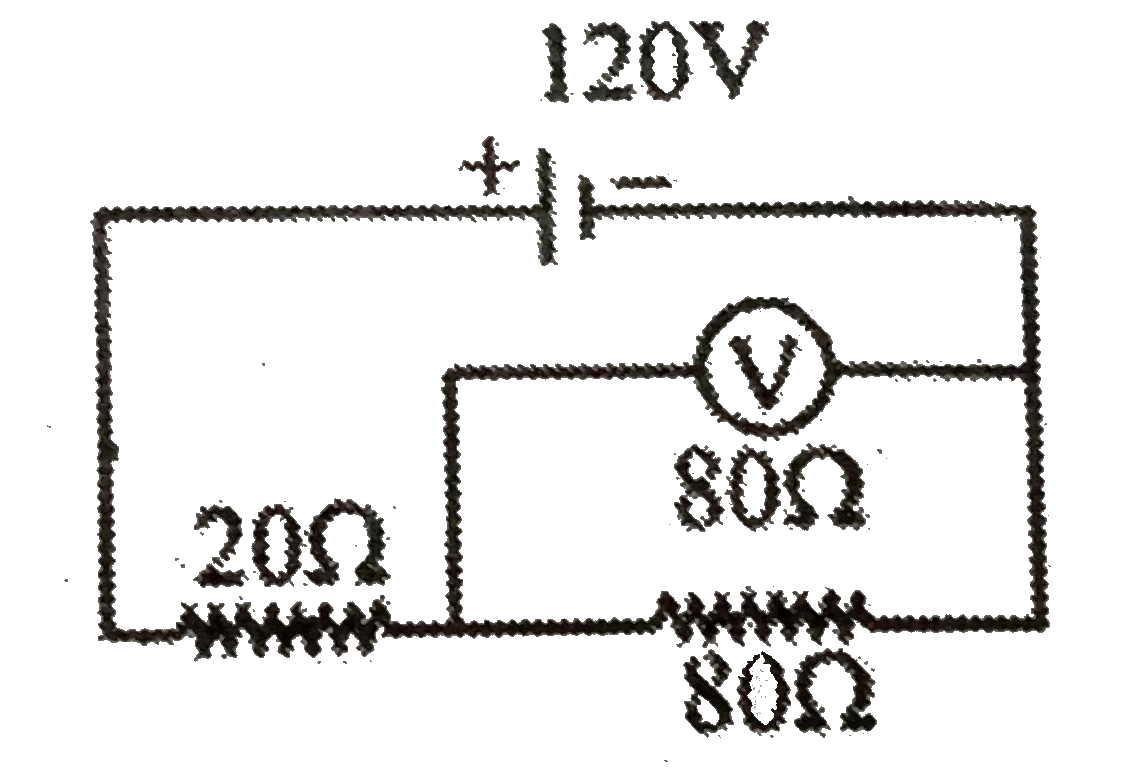 A20%B16.7%C21.2%D12.8%
A20%B16.7%C21.2%D12.8%
In a potentiometer circuit, the emf of driver cell is 2V and internal resistance is 0.5Ω. The potentiometer wire is 1m long . It is found that a cell of emf 1V and internal resistance 0.5Ω is balanced against 60 cm length of the wire. Calculate the resistance of potentiometer wire.
View SolutionA cell has an emf of 3 volt and internal resistance 2Ω. It is connected to an ammeter having resistance 2Ω and to an external resistance of 100Ω. When a voltmeter is connected across the 100Ω. Resistance, the ammeter reading is 40 mA. The resistance of the voltmeter is
View Solution(a) A cell of emf 3.4V and internal resistance 3Ω is connected to an ammeter having resistance 2Ω and to an external resistance 100Ω. When a voltmeter is connected across the 100Ω resistance the ammeter reading is 0.04A. Find the voltage read by the voltmeter and its resistance. Had the voltmeter been an ideal one, what would have its reading ?
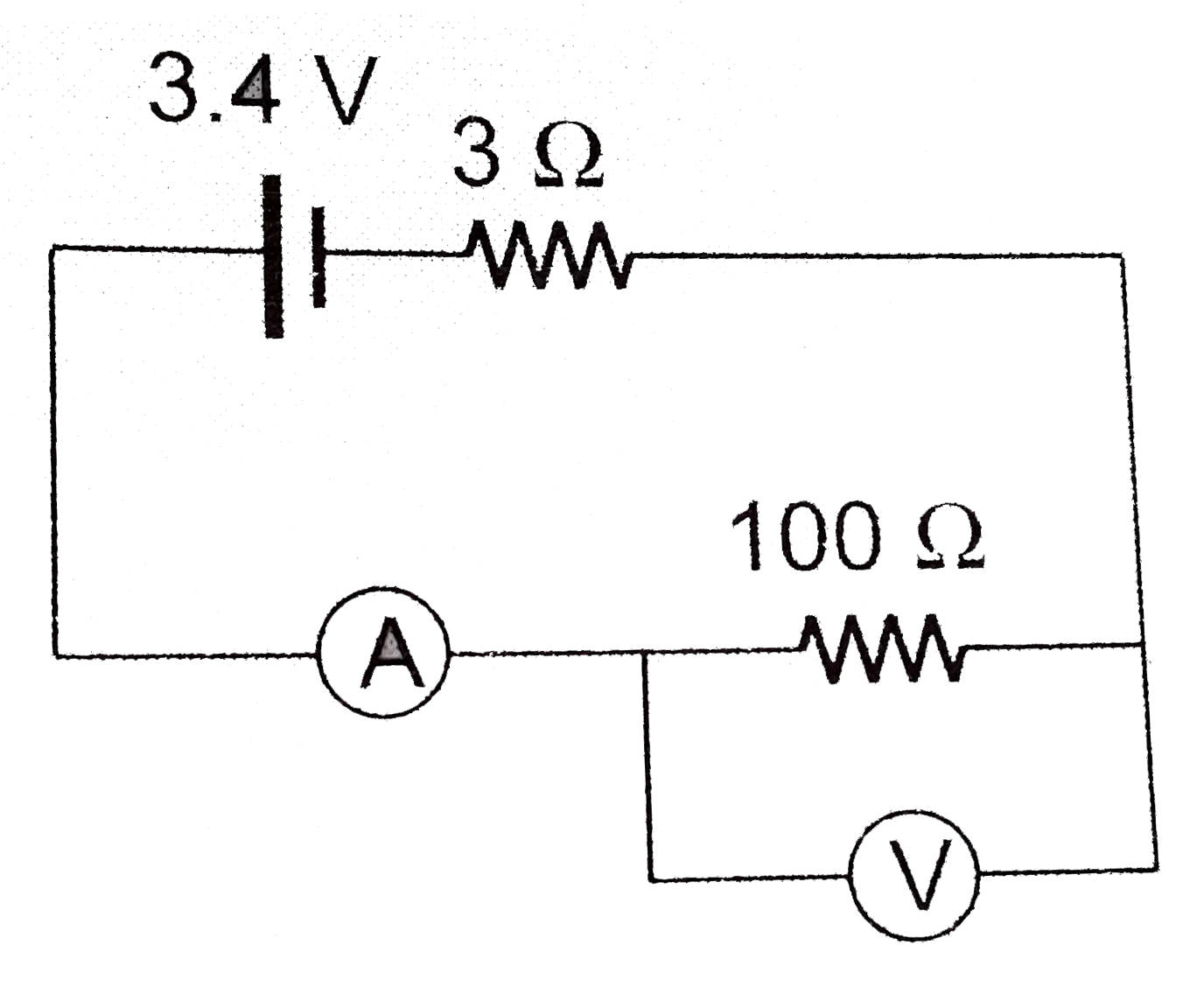
(b) Two resistances of 100Ω and 200Ω are connected in series with battery of emf 4V and negligible internal resistance. A voltmeter of resistance 200Ω is used to measure voltemeter of resistances separately. Calculate the voltmeter indicated.
( c) In the circuit shown, a voltmeter reads 30V when it is connected across the 400Ω resistance. Calculate what the same voltmeter will read when it is connected across the 300Ω resistance ?
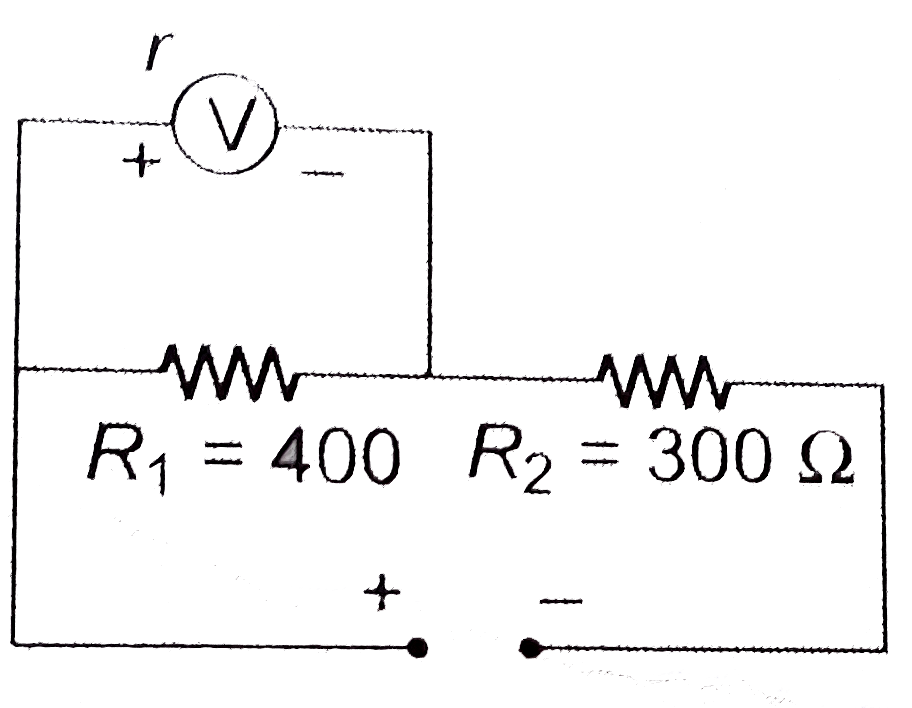
(d) An ammeter and a voltmeter are connected in series to a battery of emf E=6.0V. When a certain resistance is connected in parallel with the voltmeter. the reading of the ammeter is doubled. while voltmeter reading is reduced to half. Find the voltmeter reading after the connection of the resistance.
View SolutionThe emf of a battery is 6.0 V and its internal resistance is 1.5Ω. Its potential differences is measured by a voltmeter of resistance 1000Ω. Calculate the percentage error in the reading of emf shown by voltmeter.
View SolutionA cheap voltmeter with an internal resistance of 30Ω is connected to the terminals of a battery whose internal resistance is 5Ω and true emf 1.5 V. What would be the terminal voltage as read by the voltmeter?
View SolutionA cell of emf ε and internal resistance r gives a current of 0.5 A with an external resistance of 12Ω and a current of 0.25 A with an external resistance of 25Ω. Calculate (a) internal resistance of the cell and (b) emf of the cell.
View SolutionThe emf of a battery is 4.0 V and its internal resistance is 1.5Ω. Its potential difference is measured by a voltmeter of resistance 1000Ω. Calculate the percentage error in the reading of emf shown by voltmeter.
View Solution
