A uniform bar of mass m is supported by a pivot at its top about which the bar can swing like a pendulum. If a force F is applied perpendicular to the lower end of the bar as shown in figure, what is the value of F in order to hold the bar in equilibrium at an angle (θ) from the vertical
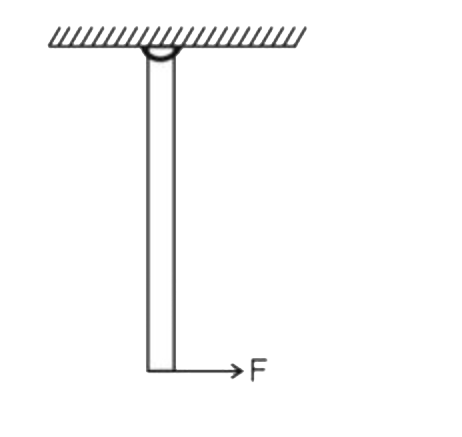
2mgsinθ
mgsinθ
mg2sinθ
mg2cosθ
The correct Answer is:C
Step by step video, text & image solution for A uniform bar of mass m is supported by a pivot at its top about which the bar can swing like a pendulum. If a force F is applied perpendicular to the lower end of the bar as shown in figure, what is the value of F in order to hold the bar in equilibrium at an angle (theta) from the vertical by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A bar of cross section A is subjected to equal and opposite tensile forces F at its ends. Consider a plane through the bar making an angle θ with a plane at right angles to the bar as shown in figure.
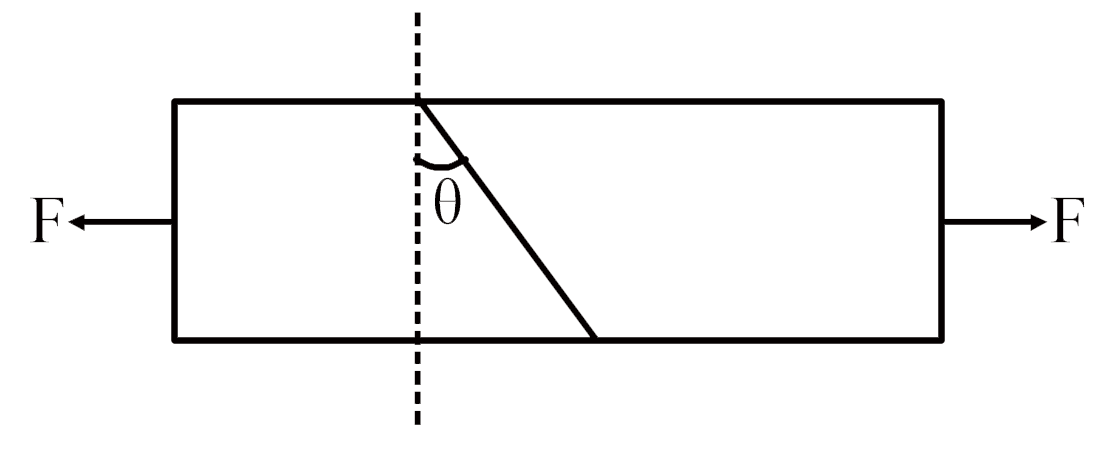
The shearing stress at the plane, in terms of F, A and θ is
View SolutionFig shows a bar of uniform cross section of area s. Equal and opposite tensile forces are applied at the ends of the bar. Each force has a magnitude F. ABCD is a plane trough the bar and inclined at angle θ with the perpendicular to the length of the bar.

Normal stress at the plane which is inclined with the plane perpendicular to the length of the bar is -
View Solution
Knowledge Check
A rod of mass m and length L is hinged at its top end. If the rod is in equilibrium making an angle of 30∘ with the vertical when a horizontal force F is applied as shown in figure, then the value of F is:
 Amg/2B2mgCmg/2√3D√3mg
Amg/2B2mgCmg/2√3D√3mgA uniform thin bar of mass 6m and length 12L is bend to make a regular hexagon. Its moment of inertia about an axis passing through the centre of mass and perpendicular to the plane of the hexagon is :
A20mL2B6mL2C125mL2D30mL2A uniform thin bar of mass 6m and length 12L is bent to make a regular hexagon. Its moment of inertia about an axis passing through the centre of mass and perpendicular to the plane of hexagon is
A20mL2B30mL2C(125)mL2D6mL2
(a) Derive the experience for the forest acting between two long parallel current carrying conductors. Hence , defined 1 A current .
(b) A bar magnet of dipole moment 3 A m2 . rests with its centre on a frictionless pivot. A force F is applied at right angles to the axis of the magnet , 10 cm from the pivot . It is observed that an external magnetic field of 0.25 T is required to hold the magnet in equilibrium at an angle of 30∘ with the field.
Calculate the value of F.
How will the equilibrium be effected if F is withdrawn?
View SolutionFig shows a bar of uniform cross section of area s. Equal and opposite tensile forces are applied at the ends of the bar. Each force has a magnitude F. ABCD is a plane trough the bar and inclined at angle θ with the perpendicular to the length of the bar.
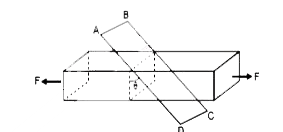
Shear stress on theplane which is inclined with the plane perpendicular to the length of the bar is
View SolutionA bar of cross section A is subjected to equal and opposite tensile forces F at its ends. Consider a plane through the bar making an angle θ with a plane at right angles to the bar as shown in figure.
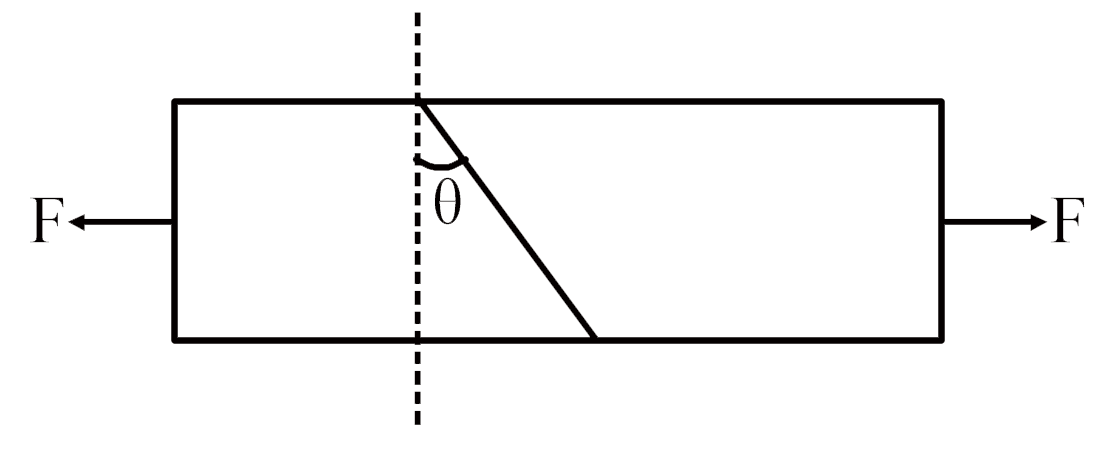
The tensile stress at this plane in terms of F, A and θ is
View SolutionIn a trapeze-shaped structure, two rigid wires of negligble mass support a conducting bar of mass m and length L as shown in Fig. A source of emf is applied to the wires so that a current I flows through the bar. A uniform magnetic field →B is perpendicular to the plane of the wires and bar.
a. Compute the current that the source of emf must provide so that there is no tension in the wires.
b. If the current is reduced to half the value computed in (a) and the plane of the structure is moved through an angle θ, compute the tension in the wires and the magnitude of the net unbalanced force on the bar at the instant it is released from this angle.

View SolutionA uniform slender bar B of mass m and length L supported by a firctionless m and length L supported by a firctionless pivot at A is released from rest at its vertical position as shown the figure. Calculate the reaction at pivot when the bar just acquires the horizontal position shown dotted.

View Solution
