For the circuit shown in the figure. The equivalent resistance between point A and B for the two cases (i) VA>VB,(ii)VB>VA respectively is……….Ωand……….Ω respectively. (D1andD2 are ideal diodes)
25,∞
50,∞
∞,25
25,25
The correct Answer is:A
To solve the problem of finding the equivalent resistance between points A and B in the given circuit with ideal diodes D1 and D2, we will analyze two cases based on the potential difference between points A and B.
Step 1: Analyze Case (i) where VA>VB
1. In this case, point A is at a higher potential than point B. This means that diode D1 (connected to point A) will be forward-biased, and diode D2 (connected to point B) will also be forward-biased.
2. Since both diodes are forward-biased, they will act as short circuits (ideal diodes have zero resistance when forward-biased).
3. The resistors R1 and R2 are connected in parallel because both diodes are conducting.
4. The formula for equivalent resistance Req for resistors in parallel is given by:
1Req=1R1+1R2
5. Substituting the values of R1 and R2 (assuming both are 50 ohms):
1Req=150+150=250=125
6. Therefore, the equivalent resistance Req is:
Req=25Ω
Step 2: Analyze Case (ii) where VB>VA
1. In this case, point B is at a higher potential than point A. This means that diode D1 will be reverse-biased and diode D2 will also be reverse-biased.
2. When diodes are reverse-biased, they act as open circuits (ideal diodes have infinite resistance when reverse-biased).
3. Since both diodes are not conducting, there is no path for current to flow between points A and B.
4. Therefore, the equivalent resistance in this case is considered to be infinite:
Req=∞Ω
Final Answers:
- For case (i) VA>VB: Req=25Ω
- For case (ii) VB>VA: Req=∞Ω
2. Since both diodes are forward-biased, they will act as short circuits (ideal diodes have zero resistance when forward-biased).
3. The resistors R1 and R2 are connected in parallel because both diodes are conducting.
4. The formula for equivalent resistance Req for resistors in parallel is given by:
1Req=1R1+1R2
5. Substituting the values of R1 and R2 (assuming both are 50 ohms):
1Req=150+150=250=125
6. Therefore, the equivalent resistance Req is:
Req=25Ω
2. When diodes are reverse-biased, they act as open circuits (ideal diodes have infinite resistance when reverse-biased).
3. Since both diodes are not conducting, there is no path for current to flow between points A and B.
4. Therefore, the equivalent resistance in this case is considered to be infinite:
Req=∞Ω
- For case (i) VA>VB: Req=25Ω
- For case (ii) VB>VA: Req=∞Ω
Topper's Solved these Questions
Similar Questions
Knowledge Check
The equivalent resistance between the points A and B, if VA>VB is
A10ΩB20ΩC30ΩD15ΩEach resistance shown in figure is 2Ω. The equivalent resistance between A and B is
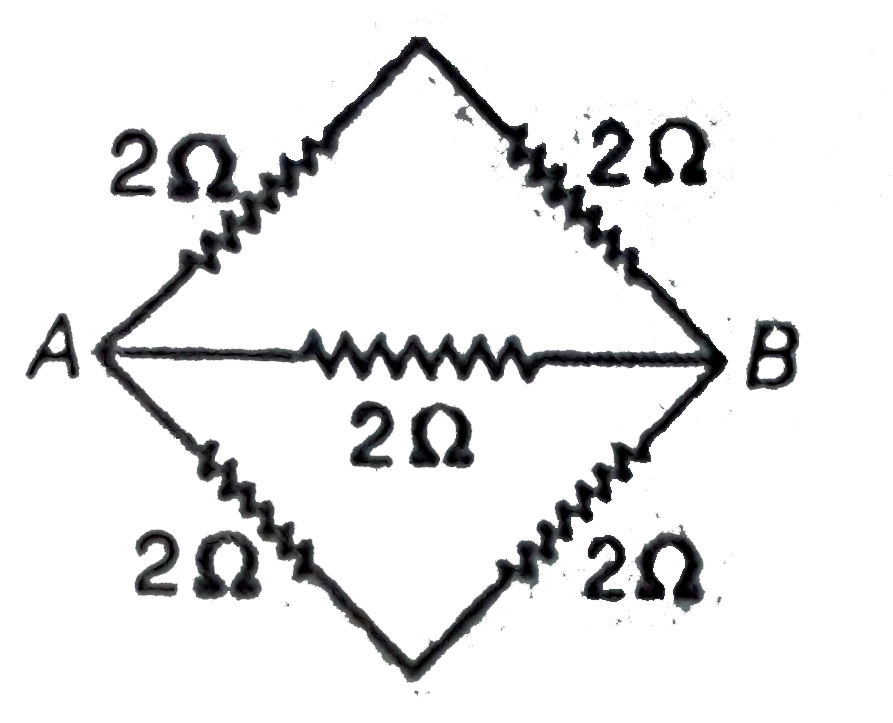 A2ΩB4ΩC8ΩD1Ω
A2ΩB4ΩC8ΩD1ΩThe equivalent resistance of the circuit shown in figure between the points A and B if VA<VB is
 A10ΩB20ΩC5ΩD40Ω
A10ΩB20ΩC5ΩD40Ω
In the circuit shown, the potential differences, V1 ( between A and B ) and V2 ( between C and D ), are
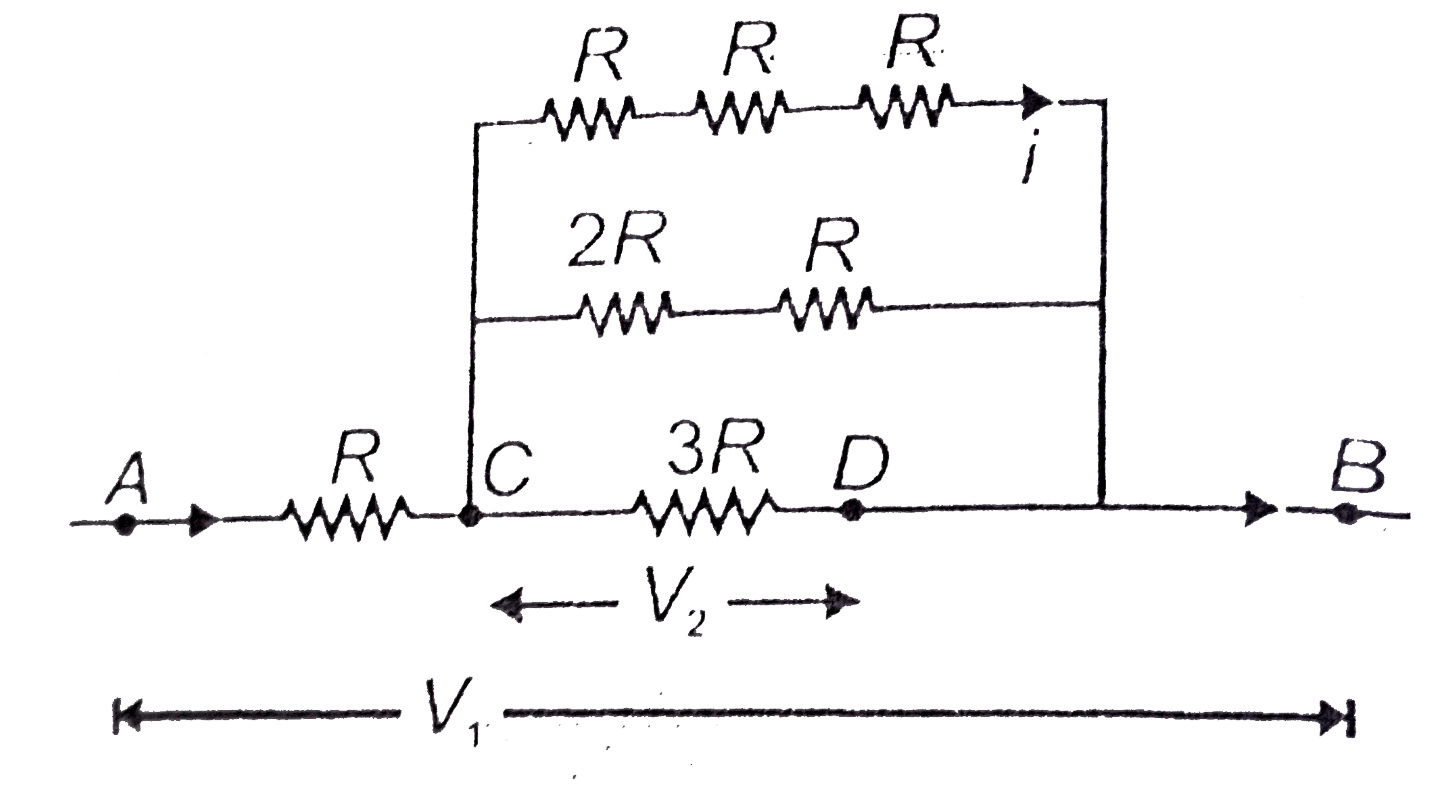
View SolutionIn the circuit shown in figure potential difference between point A and B is 16V. Find the current passing through 2Ω resistance.
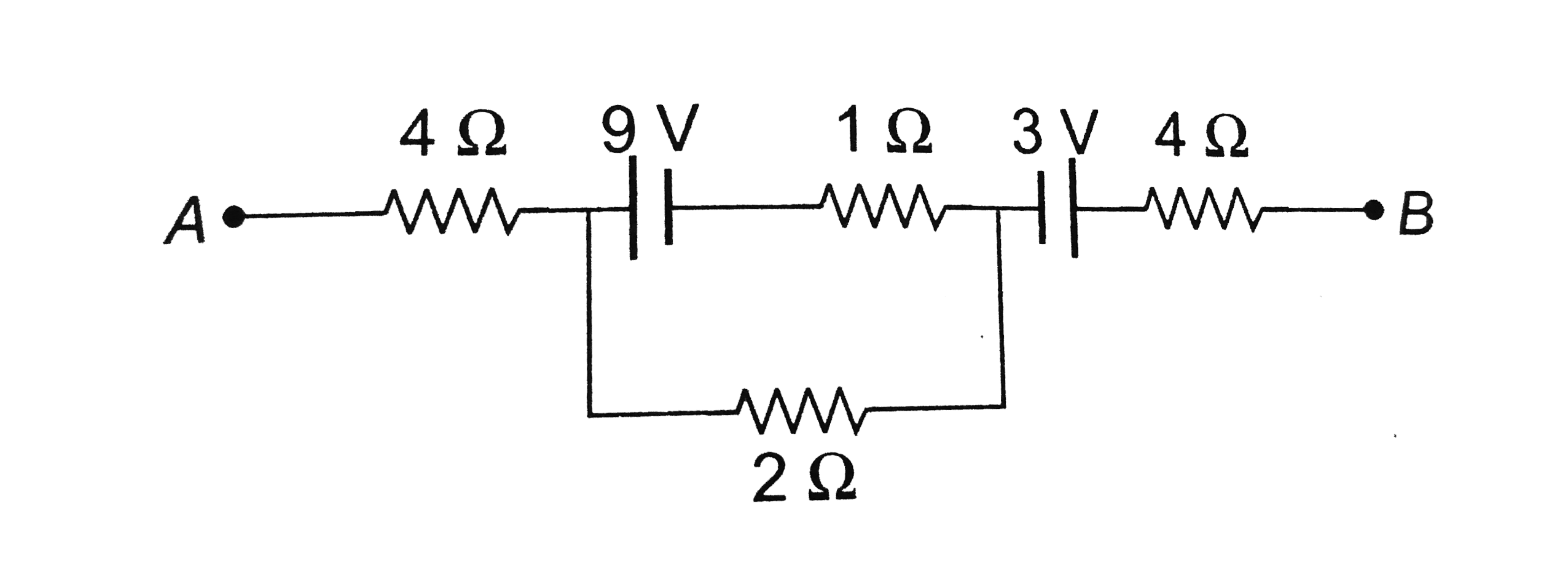
View SolutionFind the equivalent resistance of the circuit between points A and B shown in figure is (: each brach if of resistance 01Ω)
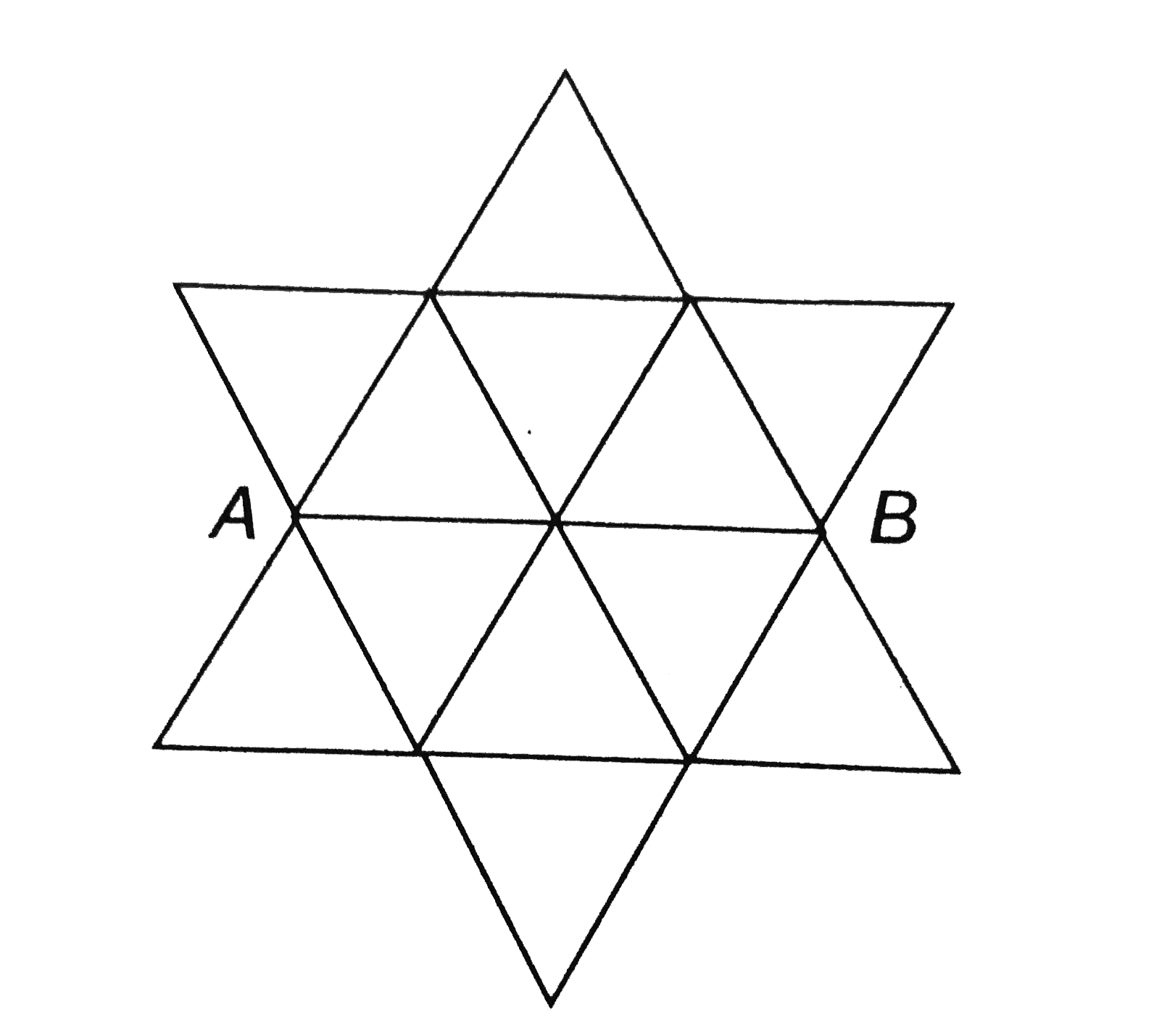
View SolutionConsider the circuit shown in the figure, the cell is ideal. The readings of the ideal voltmeters V1 and V2 in volts are respectively.

View SolutionThe potential difference (VA−VB) between the point A and B as shown in the figure is
View Solution


_PHY_E01_001_Q01.png)