Two particles P and Q are moving on circle. At a certain instant of time both the particles and diametrically opposite and P has tangential acceleration and centripetal acceleration whereas Q has only e centripetal acceleration of. At that instant acceleration of P with respect to Q is
The correct Answer is:C
To find the acceleration of particle P with respect to particle Q, we need to consider the components of their accelerations.
1. Identify the Given Accelerations:
- Particle P has:
- Tangential acceleration, atP=8m/s2
- Centripetal acceleration, acP=5m/s2
- Particle Q has:
- Centripetal acceleration, acQ=1m/s2
- Tangential acceleration, atQ=0m/s2 (since it has only centripetal acceleration)
2. Determine the Direction of Accelerations:
- For particle P:
- Centripetal acceleration points towards the center of the circle (let's assume it points in the negative x-direction).
- Tangential acceleration points in the direction of motion (let's assume it points in the positive y-direction).
- For particle Q:
- Centripetal acceleration also points towards the center of the circle (which is in the positive x-direction, since Q is diametrically opposite to P).
3. Express the Accelerations in Vector Form:
- The acceleration vector of P can be expressed as:
→aP=−5^i+8^j
- The acceleration vector of Q can be expressed as:
→aQ=−1^i+0^j
4. Calculate the Acceleration of P with Respect to Q:
- The acceleration of P with respect to Q is given by:
→aPQ=→aP−→aQ
- Substituting the values:
→aPQ=(−5^i+8^j)−(−1^i+0^j)
=(−5+1)^i+(8−0)^j
=−4^i+8^j
5. Find the Magnitude of the Relative Acceleration:
- The magnitude of the acceleration vector →aPQ is given by:
|→aPQ|=√(−4)2+(8)2
=√16+64
=√80
=4√5m/s2
Final Answer:
The acceleration of P with respect to Q is 4√5m/s2.
- Particle P has:
- Tangential acceleration, atP=8m/s2
- Centripetal acceleration, acP=5m/s2
- Particle Q has:
- Centripetal acceleration, acQ=1m/s2
- Tangential acceleration, atQ=0m/s2 (since it has only centripetal acceleration)
- For particle P:
- Centripetal acceleration points towards the center of the circle (let's assume it points in the negative x-direction).
- Tangential acceleration points in the direction of motion (let's assume it points in the positive y-direction).
- For particle Q:
- Centripetal acceleration also points towards the center of the circle (which is in the positive x-direction, since Q is diametrically opposite to P).
- The acceleration vector of P can be expressed as:
→aP=−5^i+8^j
- The acceleration vector of Q can be expressed as:
→aQ=−1^i+0^j
- The acceleration of P with respect to Q is given by:
→aPQ=→aP−→aQ
- Substituting the values:
→aPQ=(−5^i+8^j)−(−1^i+0^j)
=(−5+1)^i+(8−0)^j
=−4^i+8^j
- The magnitude of the acceleration vector →aPQ is given by:
|→aPQ|=√(−4)2+(8)2
=√16+64
=√80
=4√5m/s2
The acceleration of P with respect to Q is 4√5m/s2.
Topper's Solved these Questions
Similar Questions
A particle is moving on a circular path of radius 1m. It starts from rest,its tangential acceleration is √3t .The time after which the acceleration of the particle makes an angle of 30∘ with centripetal acceleration is (n)23s .Find the value of n.
View SolutionA force of 10N gives a mass m1 an acceleration of 10m/s2 and a mass m2 an acceleration of 20m/s2 What acceleration would it give if both the masses are tid together ?
View Solution
Knowledge Check
If acceleration of A is 2m/s2 to left and acceleration of B is 1m/s2 to left, then acceleration of C is-
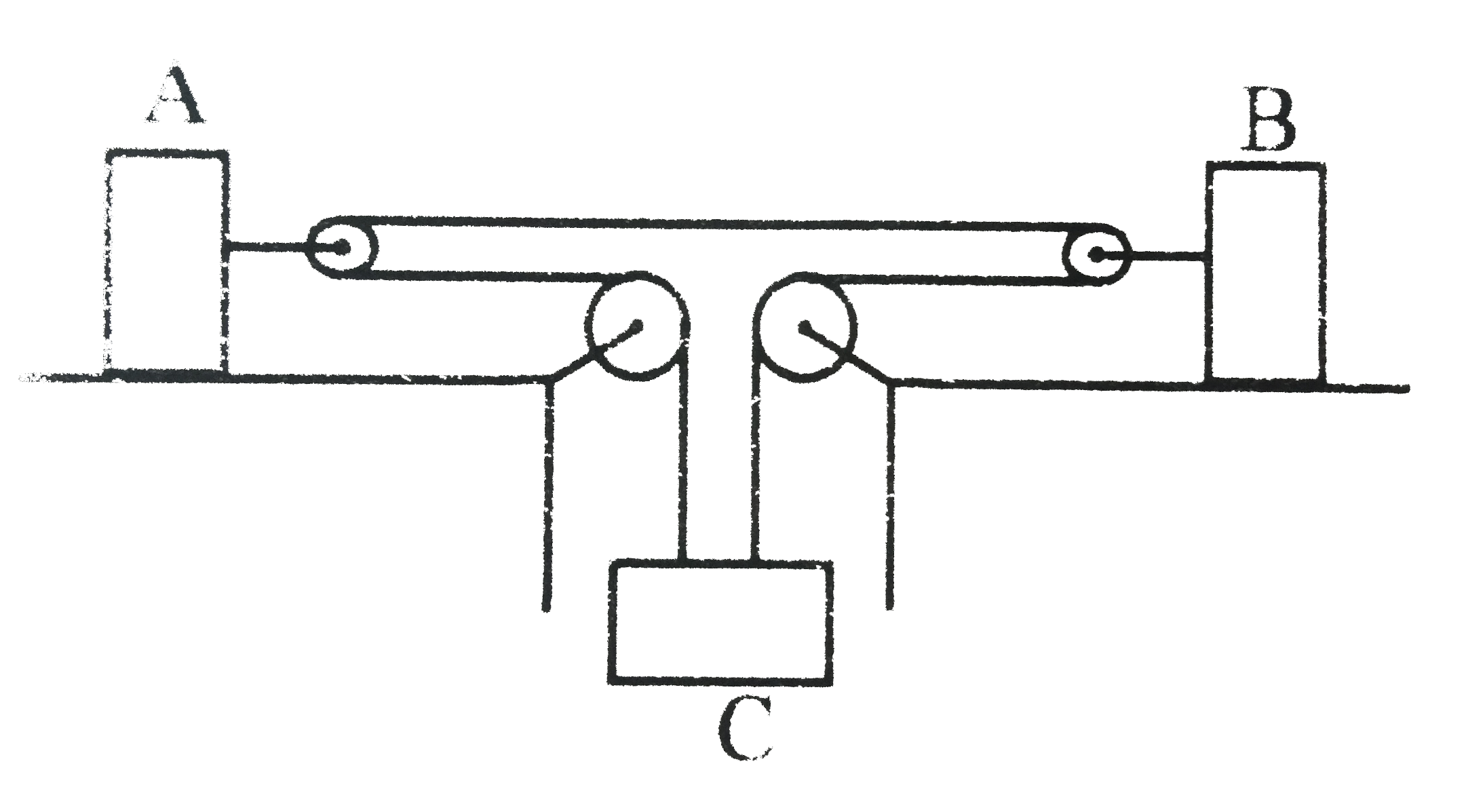 A1m/s2upwardsB1m/s2downwC2m/s2downwardsD2m/s2upwards
A1m/s2upwardsB1m/s2downwC2m/s2downwardsD2m/s2upwardsA ball is moving in a circular path of radius 5m. If tangential acceleration at any instant is 10 m/s2 and the net acceleration makes an angle 30∘ with the centripetal acceleration, then the instantaneous speed is
A50√3m/sB9.3m/sC6.6m/sD5.4m/sTwo bodies are moving with constant speed v clockwise and are initially diagonally opposite. The particle B now acheives a tangential acceleration of a m/s2. Then :
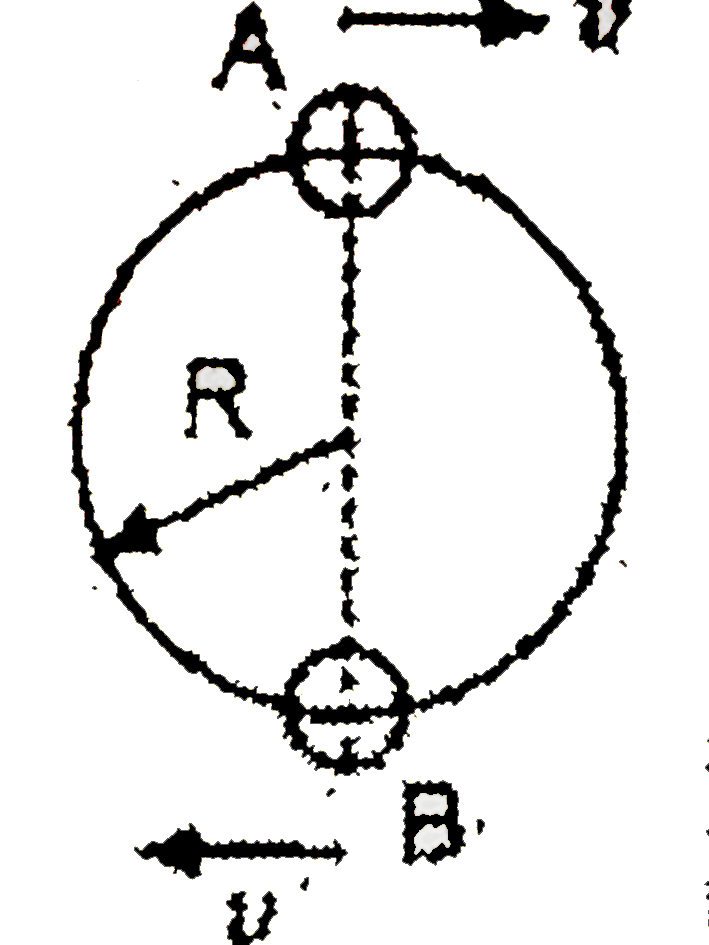 Athen collide after time √πRaBthey collide after time √2πRaCrelative velocity just before collision is √πaRDrelative velocity just before collision is √πaR
Athen collide after time √πRaBthey collide after time √2πRaCrelative velocity just before collision is √πaRDrelative velocity just before collision is √πaR
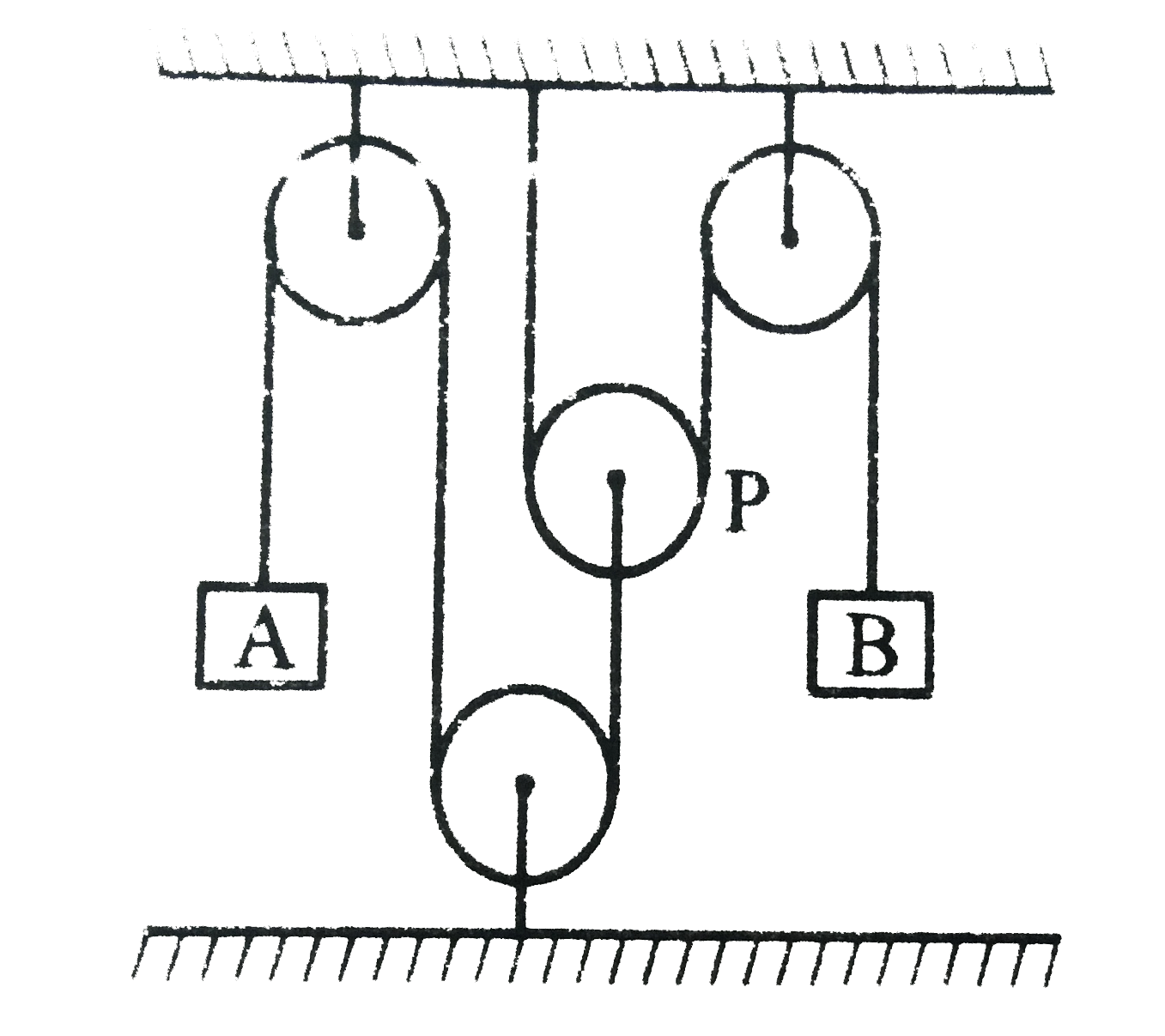
Find the acceleration of movable pulled P and block B if acceleration of block A=1m/s2⏐↓.
View SolutionA force of 2N gives a mass m1 an acceleration of 5m/s2 and a mass m2 an acceleration of 7m/s2. What acceleration would be produced if both the masses are tied together?
View SolutionIn the figure acceleration of A is 1m/s2 upward, acceleration of B is 7m/s2 upward acceleration of C is 2m/s2 upward. The acceleration of D will be.

View SolutionA force of 5N gives a mass m1, an acceleration of m/s2, and a mass m2, an acceleration of 24m/s2. What acceleration would it give if both the masses are tied together?
View SolutionPoint A on the rod AB has an acceleration of 5m/s2 and a velocity of 6m/s at an instant as shown in the figure. The acceleration of the end B at the same moment is:

View Solution
