For a circular cardboard of uniform thickness and mass M, a square disc of the maximum possible are is cut. If the moment of inertia of the square with the moment of inertial of the square with the axis of rotation at the centre and perpendicular to the plane of the disc is Ma26, the radius of the circular cardboard is
√2a
a√2
2a
2√2a
The correct Answer is:B
To solve the problem, we need to find the radius of the circular cardboard from which a square disc of maximum possible area is cut. We are given that the moment of inertia of the square is Ma26.
1. Define Variables:
- Let M be the mass of the circular cardboard.
- Let r be the radius of the circular cardboard.
- Let b be the side length of the square cut from the circular cardboard.
- The area of the square is A=b2.
2. Moment of Inertia of the Square:
- The moment of inertia of the square about an axis through its center and perpendicular to its plane is given by:
I=Mb26
- According to the problem, this is equal to Ma26. Therefore, we can equate:
Mb26=Ma26
- Canceling M6 from both sides gives:
b2=a2
3. Finding the Maximum Size of the Square:
- The maximum size of the square that can be cut from the circular cardboard occurs when the square is inscribed in the circle.
- The diagonal of the square is equal to the diameter of the circle:
Diagonal of square=b√2=2r
- Therefore, we can express b in terms of r:
b=2r√2=r√2
4. Substituting b into the Moment of Inertia Equation:
- Substitute b=r√2 into the equation b2=a2:
(r√2)2=a2
- This simplifies to:
2r2=a2
- Rearranging gives:
r2=a22
5. Finding the Radius r:
- Taking the square root of both sides, we find:
r=a√2
Final Result:
The radius of the circular cardboard is:
r=a√2
- Let M be the mass of the circular cardboard.
- Let r be the radius of the circular cardboard.
- Let b be the side length of the square cut from the circular cardboard.
- The area of the square is A=b2.
- The moment of inertia of the square about an axis through its center and perpendicular to its plane is given by:
I=Mb26
- According to the problem, this is equal to Ma26. Therefore, we can equate:
Mb26=Ma26
- Canceling M6 from both sides gives:
b2=a2
- The maximum size of the square that can be cut from the circular cardboard occurs when the square is inscribed in the circle.
- The diagonal of the square is equal to the diameter of the circle:
Diagonal of square=b√2=2r
- Therefore, we can express b in terms of r:
b=2r√2=r√2
- Substitute b=r√2 into the equation b2=a2:
(r√2)2=a2
- This simplifies to:
2r2=a2
- Rearranging gives:
r2=a22
- Taking the square root of both sides, we find:
r=a√2
The radius of the circular cardboard is:
r=a√2
Topper's Solved these Questions
Similar Questions
Calculate the moment of inertia of a disc of radius R and mass M, about an axis passing through its centre and perpendicular to the plane.
View SolutionA disc has mass 9 m. A hole of radius R/3 is cut from it as shown in the figure. The moment of inertia of remaining part about an axis passing through the centre 'O' of the disc and perpendicular to the plane of the disc is :

View Solution
Knowledge Check
The moment of inertia of a circular disc about an axis passing through the circumstances perpendicular to the plane of the disc is
A(MR2B32MR[^(2)CMR22D54MR2The moment of Inertia of an incomplete disc of mas M and radius R as shown in figure about the axis passing through the centre and perpendicular to the plane of the disc is:
 AMR22B7MR212C7MR26D5MR212
AMR22B7MR212C7MR26D5MR212The moment of inertia of a thin square plate ABCD of uniform thickness about an axis passing through the centre O and perpendicular to plate is
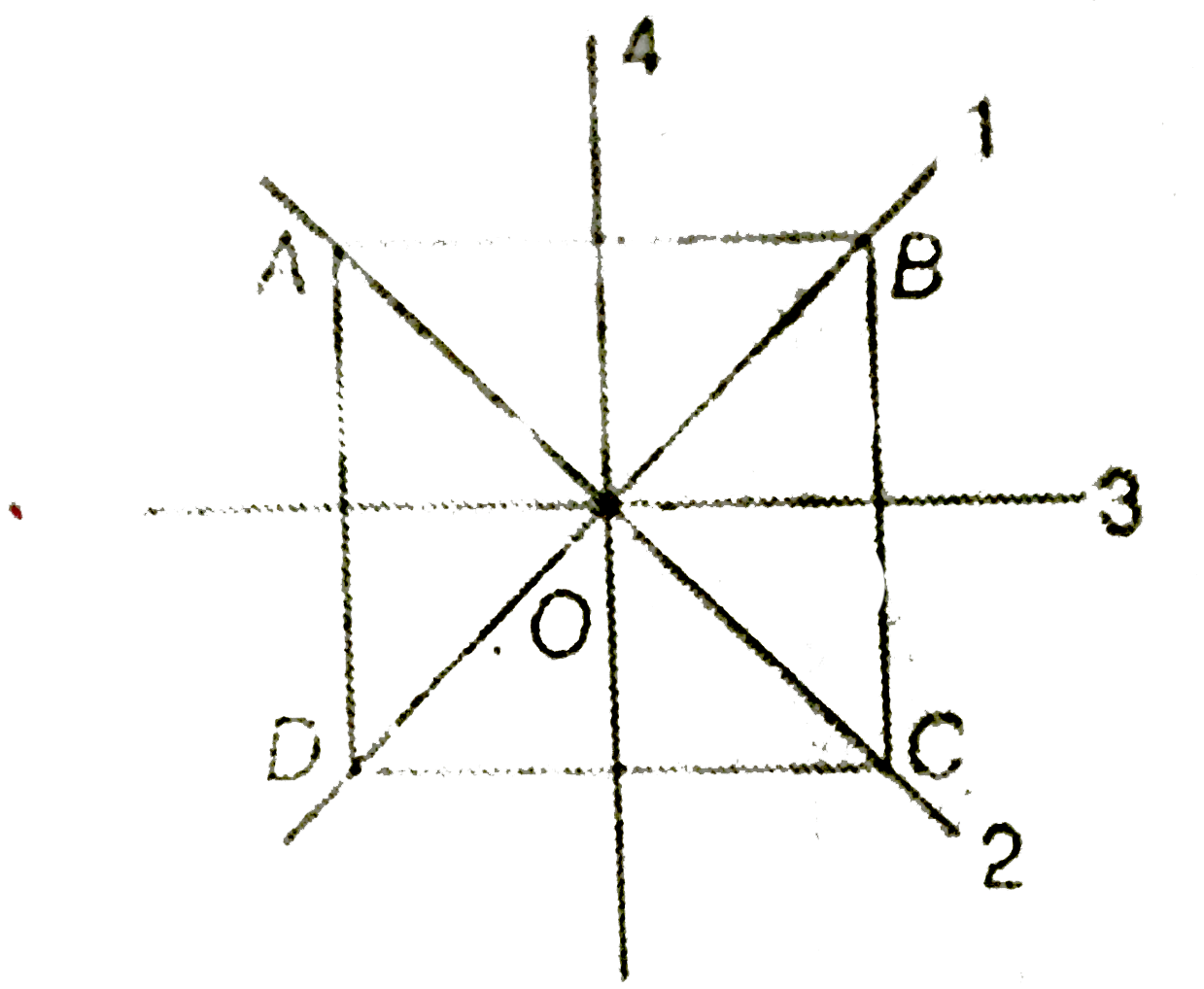 Al1+l2Bl2+l3Cl1+l3Dl3+l4
Al1+l2Bl2+l3Cl1+l3Dl3+l4
The moment of inertia of a copper disc, rotating about an axis passing through its centre and perpendicular to its plane
View SolutionThe diameter of a thin circular disc of mass 2 kg is 0.2 m. Its moment of inertia about an axis passing through the edge and perpendicular to the plane of the disc is
View SolutionThe diagram shows a uniform disc of mass M & radius 'a', if the moment of inertia of the disc about the axis XY is I, its moment of inertia about an axis through O and perpendicular to the plane of the disc is

View SolutionThe moment of inertia of a thin square plate ABCD, as shown A in the figure, of uniform thickness about an axis passing through the centre O and perpendicular to the plane of
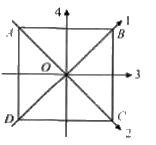
View SolutionThe moment of inertia of a circular disc about an axis passing through its centre and perpendicular to the plane is 4kgm2 . Its moment of inertia about the diameter is
View Solution
