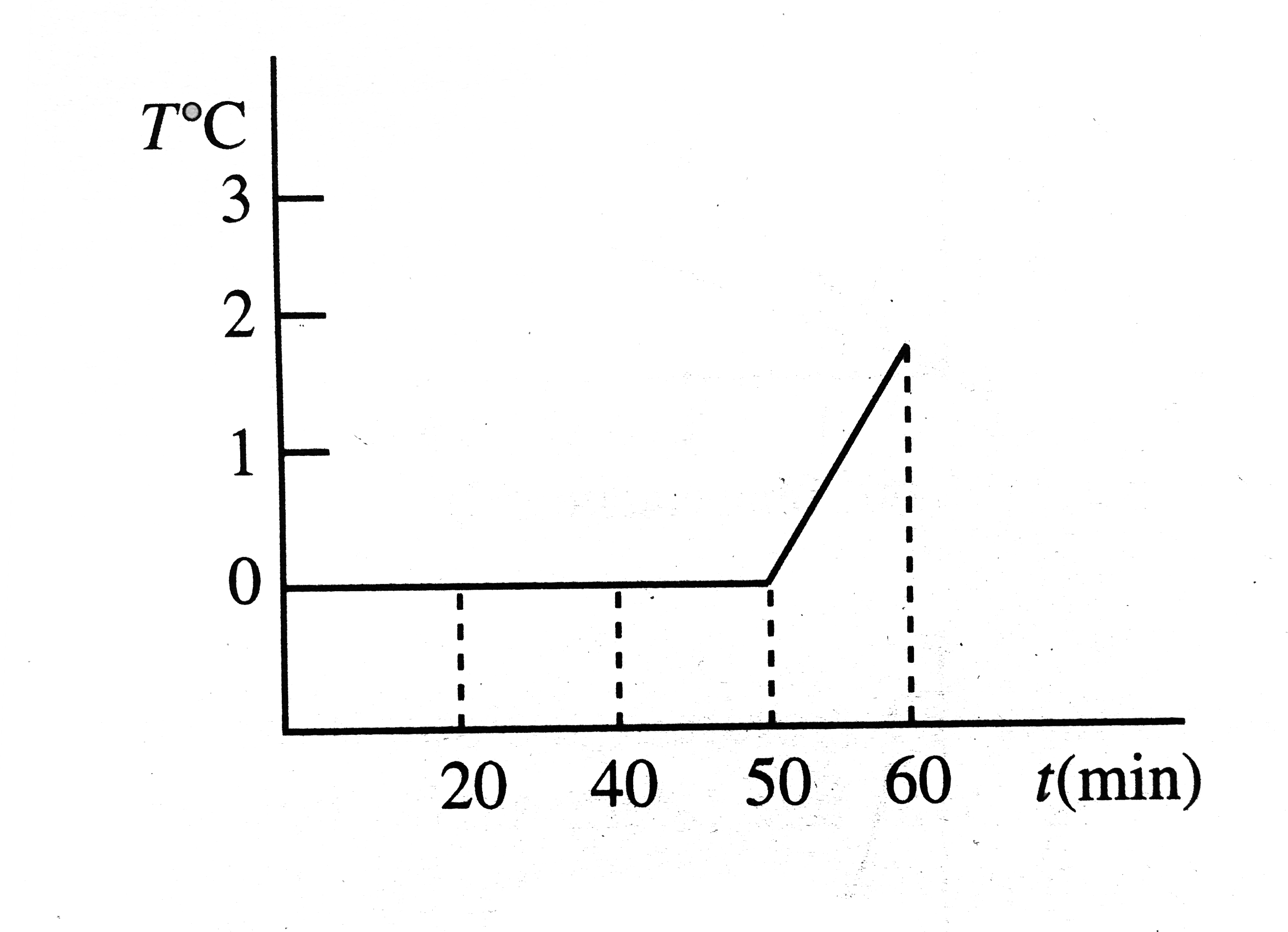
A cooking vessel on a slow burner contains 5 kg of water and an unknown mass of ice in equilibrium at at time . The temperature of the mixture is measured at various times and the result is plotted as shown in Fig. During the first 50 min the mixture remains at . From 50 min to 60 min, the temperature increases to Neglecting the heat capacity of the vessel, the initial mass of the ice is
The correct Answer is:B
Step by step video, text & image solution for A cooking vessel on a slow burner contains 5 kg of water and an unknown mass of ice in equilibrium at 0^@C at time t=0. The temperature of the mixture is measured at various times and the result is plotted as shown in Fig. During the first 50 min the mixture remains at 0^@C. From 50 min to 60 min, the temperature increases to 2^@C Neglecting the heat capacity of the vessel, the initial mass of the ice is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
If 2g ice at 00C is dropped into 10g water at 800C then temperature of mixture is
View SolutionA container contains 5 kg of water at 0∘C mixed to an unknown mass of ice in thermal equilibrium. The water equivalent of the container is 100 g. At time t = 0, a heater is switched on which supplies heat at a constant rate to the container. The temperature of the mixture is measured at various times and the result has been plotted in the given figure. Neglect any heat loss from the mixture – container system to the surrounding and calculate the initial mass of the ice.
Given: Sp. latent heat of fusion of ice is Lf=80calg−1
Sp. heat capacity of water =1calg−1.∘C−1
View Solution
Knowledge Check
5 g of ice at 0∘C and 20 g of water at 45∘C are mixed. The temperature of the mixture will be
A10∘CB20∘CC30∘CD40∘COne gram of ice at 0∘C is added to 5 gram of water at 10∘C. If the latent heat of ice be 80 cal/g, then the final temperature of the mixture is -
A5∘CB0∘CC−5∘CDNone of the above100g ice at 0∘C is mixed with 100g water at 100∘C. The resultant temperature of the mixture is
A10∘CB20∘CC30∘CD40∘C
15 g ice at 0∘C is mixed with 10 g water at 40∘C. Find the temperature of mixture. Also, find mass of water and ice in the mixture.
View Solution1g steam at 100∘C is passed in an insulating vessel having 1g ice at 0∘C. Find the equilibrium composition of the mixture. (Neglecting heat capacity of the vessel).
View SolutionA vessel of volume V=201 contains a mixture of hydrogen and helium at a temperature t=20∘C and pressure p=2.0atm. The mass of the mixture is equal is equal to m=5.0g. Find the ratio of the mass of hydrogen to that of helium in the given mixture.
View SolutionHot water cools from 60∘C to 50∘C in the first 10 min and to 42∘C in the next 10 min. The temperature of the surrounding is
View SolutionA vessel contains 10–1kg of ice at 0∘C. Now steam is passed into the vessel to melt ice. Neglecting the thermal capacity of the vessel, find the mass of water in the vessel when all ice melts into water.
View Solution
