A balloon is rising vertically upwards. An an instant, an observation on the ground, whose distance from the balloon is 100 meters, sees the balloon at an angle of elevation of 30∘. If the balloon rises further vertically to a point where the angle of elevation as seen by the observer is 45∘, then its height (in meters) from the ground is
(Take √3=1.73)
The correct Answer is:36.5
To solve the problem, we will break it down step by step.
Step 1: Understanding the situation
We have an observer on the ground who sees a balloon at an angle of elevation of 30∘ when it is 100 meters away horizontally. We need to find the height of the balloon when the angle of elevation changes to 45∘.
Step 2: Setting up the first triangle
Let’s denote:
- The height of the balloon at the first observation as h1.
- The horizontal distance from the observer to the balloon as d=100 meters.
Using the angle of elevation 30∘:
tan(30∘)=h1d
Since tan(30∘)=1√3, we can write:
1√3=h1100
Thus,
h1=100√3=100×1.733≈57.67 meters
Step 3: Setting up the second triangle
Now, when the balloon rises further, the angle of elevation becomes 45∘. Let the new height of the balloon be h2.
Using the angle of elevation 45∘:
tan(45∘)=h2d
Since tan(45∘)=1, we have:
1=h2100
Thus,
h2=100 meters
Step 4: Finding the total height from the ground
Now, we need to find the total height of the balloon from the ground when it is at the 45∘ angle of elevation.
The height of the balloon when it was first observed was h1≈57.67 meters. The balloon has risen from this height to h2=100 meters.
Step 5: Conclusion
The total height of the balloon from the ground when the angle of elevation is 45∘ is:
h2=100 meters
Final Answer
The height of the balloon from the ground is 100 meters.
---
We have an observer on the ground who sees a balloon at an angle of elevation of 30∘ when it is 100 meters away horizontally. We need to find the height of the balloon when the angle of elevation changes to 45∘.
Let’s denote:
- The height of the balloon at the first observation as h1.
- The horizontal distance from the observer to the balloon as d=100 meters.
tan(30∘)=h1d
Since tan(30∘)=1√3, we can write:
1√3=h1100
Thus,
h1=100√3=100×1.733≈57.67 meters
Now, when the balloon rises further, the angle of elevation becomes 45∘. Let the new height of the balloon be h2.
tan(45∘)=h2d
Since tan(45∘)=1, we have:
1=h2100
Thus,
h2=100 meters
Now, we need to find the total height of the balloon from the ground when it is at the 45∘ angle of elevation.
The total height of the balloon from the ground when the angle of elevation is 45∘ is:
h2=100 meters
The height of the balloon from the ground is 100 meters.
Topper's Solved these Questions
Similar Questions
The value of the integral ∫40{x3−6x2+12x−4+(x−2)cos(x−2)}dx is equal to
View SolutionFor f(x)=x3+bx2+cx+d, if b2>4c>0 and b,c,d∈R, then f(x)
View SolutionSuppose,there are two windows in a house.A window of the house is at a height of 1.5 m above the ground and the other window is 3 m vertically above the lower window.Anil and Sanjeev are sitting inside the two windows,At an instant the angles of elevation of two balloon from these windows are observed at 45^@ and 30^@,respectively. 1. Find the height of the balloon from the ground. 2. Among sanjeev and anil,who is more closer to the balloon. 3. If balloon is moving towards the building, then will both the angle of elevation remain same?
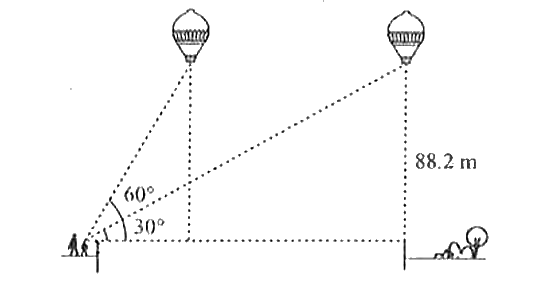
View SolutionA 1.2m tall girl spots a balloon moving with the wind in a horizontal line at a height of 88.2m from the ground. The angle of elevation of the balloon from the eyes of the girl at any instant is 60∘. After some time, the angle of elevation reduces to 30∘ ( see Figure ) . Find the distance travelled by the balloon during the interval.
View Solutionএকটি বেলুন ত্বরণসহ ওপরের দিকে উঠছে। ভূমি থেকে বেলুনটির উচ্চতা যখন 50.4m তখন বেলুন থেকে একটি পাথর ফেলা হল। পাথরটির 6s পরে ভূমি স্পর্শ করল। পাথরটি ফেলার মুহূর্তে বেলুনটির বেগ কত ছিল?
View Solutionஒரு பலூனானது செங்குத்தாக மேல் நோக்கி 10 மீ/வி வீதத்தில் செல்கிறது. பலூன் செலுத்தப்பட்ட இடத்திலிருந்து 40 மீ தொலைவில் இடமிருந்து ஒருவர் இதனைப் பார்க்கிறார். பலூனின் ஏற்றக் கோணத்தில் ஏற்படும் மாறுபாட்டு வீதத்தை பலூன் தரையிலிருந்து 30 மீட்டர் உயரத்தில் இருக்கும் போது காண்க.
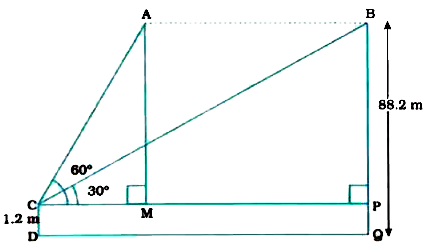
View SolutionA 1.2 m tall girl spots a balloon moving with the wind in a horizontal line at a height of 88.2 m from the ground. The angle of elevation of the balloon from the eyes of the girl at any instant is 60∘. After some time, the angle of elevation reduces to 30∘ (see figure below). find the distance travelled by the balloon during the interval.
View Solution4 मी/मिनट की सर से निचे आ रहे गुब्बारे का धरातल पर स्थित किसी बिंदु से उन्नयन कोण 45∘ है जो 10 मिनट बाद 30∘ हो जाता है। गुब्बारा,प्रेक्षक से कितनी दुरी पर जमीन पर पहुंचेगा?
View SolutionA 1.2m tall girl spots a balloon moving with the wind in a horizontal line at a height of 88.2 m from the ground. The angle of elevation of the balloon from the eyes of the girl at any instant is 60∘. After some time, the angle of elevation reduces to 30∘ (see the given figure). FInd the distance travelled by the balloon during the interval.
View SolutionThe height of a hill is 3300 mts. From the point p on the ground the angle of elevation of the top of the hill is 60∘. A balloon is moving with constant speed vertically upwards from P. After 5 Minutes of its movement a person sitting in it observers the angle of elevation of the top of hill as 30∘. The speed of balloon is
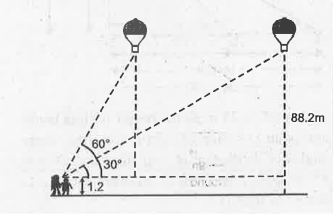
View SolutionA 1.2 m tall girl spots a balloon moving with the wind in a horizontal line at a height of 88.2 m from the ground. The angle of elevation of the balloon from the eyes of the girl at any instant is 60∘. After some time, the angle of elevation reduces to 30∘ (see fig.). Find the distance travelled by the balloon during the interval.
View SolutionA 1.4m tall girl sports a balloon moving with the wind in a horizontal line at a height of 91.4m from the ground. The angle of elevation of the balloon from the eyes of the girl at that instant is 60∘ . After some time ,the angle of elevation reduces to 30∘. Find the distance travelled by the balloon during that interval. Take √3=1.732.
View SolutionAn observer spots a balloon moving with the wind in a horizontal line at a height of 105 m from the ground. The angle of elevation of the balloon after sometime reduces from 60% to 30%. Find the distance travelled by the balloon during the interval.
View SolutionA stationary balloon is observed from three points A, B and C on the plane groundand is found that its angle of elevation from each point is 60∘. If ∠ABC=30∘ and AC = 5 meters, then the height of the balloon from the ground is
View SolutionA balloon is rising vertically upwards. An an instant, an observation on the ground, whose distance from the balloon is 100 meters, sees the balloon at an angle of elevation of 30∘. If the balloon rises further vertically to a point where the angle of elevation as seen by the observer is 45∘, then its height (in meters) from the ground is
(Take √3=1.73)
View Solution
