A body oa mass M at rest explodes into three pieces, two of which of mass (M/4) each are thrown- off in perpendicular directions with velocities of 6ms−1 and 8ms−1 respectively. The third piece will be thrown-off with a velocity of
1.5ms−1
2ms−1
5ms−1
3ms−1
The correct Answer is:(3)
To solve the problem step by step, we will apply the principle of conservation of momentum.
Step 1: Understand the Problem
We have a body of mass M that is initially at rest. Upon explosion, it breaks into three pieces:
- Two pieces of mass M4 each.
- One piece of mass M2 (since M−2×M4=M2).
The two pieces are thrown off in perpendicular directions with velocities 6m/s and 8m/s.
Step 2: Set Up the Conservation of Momentum Equation
Since the initial momentum of the system is zero (the body is at rest), the final momentum must also equal zero:
Initial Momentum=Final Momentum
0=M1→V1+M2→V2+M3→V3
Where:
- M1=M4, →V1=6m/s^i
- M2=M4, →V2=8m/s^j
- M3=M2, →V3 is unknown.
Step 3: Write the Momentum Vectors
Substituting the values into the momentum equation:
0=(M4⋅6^i)+(M4⋅8^j)+(M2→V3)
This simplifies to:
0=6M4^i+8M4^j+M2→V3
Step 4: Simplify the Equation
Now, we can simplify the equation:
0=3M2^i+2M^j+M2→V3
Step 5: Isolate →V3
Rearranging gives:
M2→V3=−3M2^i−2M^j
Dividing through by M2 (assuming M≠0):
→V3=−3^i−4^j
Step 6: Calculate the Magnitude of →V3
To find the magnitude of →V3:
|→V3|=√(−3)2+(−4)2=√9+16=√25=5m/s
Conclusion
The third piece will be thrown off with a velocity of 5m/s.
---
We have a body of mass M that is initially at rest. Upon explosion, it breaks into three pieces:
- Two pieces of mass M4 each.
- One piece of mass M2 (since M−2×M4=M2).
Since the initial momentum of the system is zero (the body is at rest), the final momentum must also equal zero:
Initial Momentum=Final Momentum
0=M1→V1+M2→V2+M3→V3
- M1=M4, →V1=6m/s^i
- M2=M4, →V2=8m/s^j
- M3=M2, →V3 is unknown.
Substituting the values into the momentum equation:
0=(M4⋅6^i)+(M4⋅8^j)+(M2→V3)
This simplifies to:
0=6M4^i+8M4^j+M2→V3
Now, we can simplify the equation:
0=3M2^i+2M^j+M2→V3
Rearranging gives:
M2→V3=−3M2^i−2M^j
Dividing through by M2 (assuming M≠0):
→V3=−3^i−4^j
To find the magnitude of →V3:
|→V3|=√(−3)2+(−4)2=√9+16=√25=5m/s
The third piece will be thrown off with a velocity of 5m/s.
Topper's Solved these Questions
- WORK , ENERGY & POWER BOOK - NARAYNACHAPTER - WORK , ENERGY & POWER EXERCISE - EXERCISE -III
54 Videos
- WORK , ENERGY & POWER BOOK - NARAYNACHAPTER - WORK , ENERGY & POWER EXERCISE - EXERCISE IV
43 Videos
- WORK , ENERGY & POWER BOOK - NARAYNACHAPTER - WORK , ENERGY & POWER EXERCISE - EXERCISE -II (C.W)
75 Videos
- WAVESBOOK - NARAYNACHAPTER - WAVESEXERCISE - Exercise-IV
56 Videos
- WORK POWER AND ENERGYBOOK - NARAYNACHAPTER - WORK POWER AND ENERGYEXERCISE - Level-VI (Integer)
12 Videos
Similar Questions
A body of mass 4m at rest explodes into three pieces. Two of the pieces each of mass m move with a speed v each in mutually perpendicular directions. The total kinetic energy released is
View SolutionA particle of mass 4m explodes into three pieces of masses m,m and 2m The equal masses move along X-axis and Y-axis with velocities 4ms−1 and 6ms−1 respectively. The magnitude of the velocity of the heavier mass is
View Solution
Knowledge Check
A body of mass M at rest explodes into three pieces, two of which of mass M//4 each are thrown off in prependicular directions eith velocities of 3/s and 4m/s respectively. The third piece willl be thrown off with a velocity of
A1.5m/sB2.0m/sC2.5m/sD3.0m/sA body of mass M at rest explodes into 3 pieces, A,B and C of masses M4,M4 and M2 respectively. A and B move in perpendicular directions with velocities 5m/s and 12 m/s respectively. What is the speed of the third piece?
A3.5m/sB5.5m/sC6.5m/sD8m/sA body of mass 4m at rest explodes into three fragments. Two of the fragments each of mass m move with speed v in mutually perpendicular directions. Total energy released in the process is
Amv2B32mv2C2mv2D3mv2
A stationary body of mass 3 kg explodes into three equal pieces. Two of the pieces fly off in two mutually perpendicular directions, one with a velocity of 3ˆims1 and the other with a velocity of 4ˆjms−1 . - If the explosion occurs in 10–4s, the average force acting on the third piece in newton is
View SolutionAn explosion blows a rock into three pieces Two pieces whose masses are 200 kg and 100 kg go off at 90∘ to eachother with a velocity of 8m/s and 12m/s respectively If the third piece flies off with a velocity of25m/s then calculate the mass of this piece and indicate the direction of flight of this piece in a diagram.
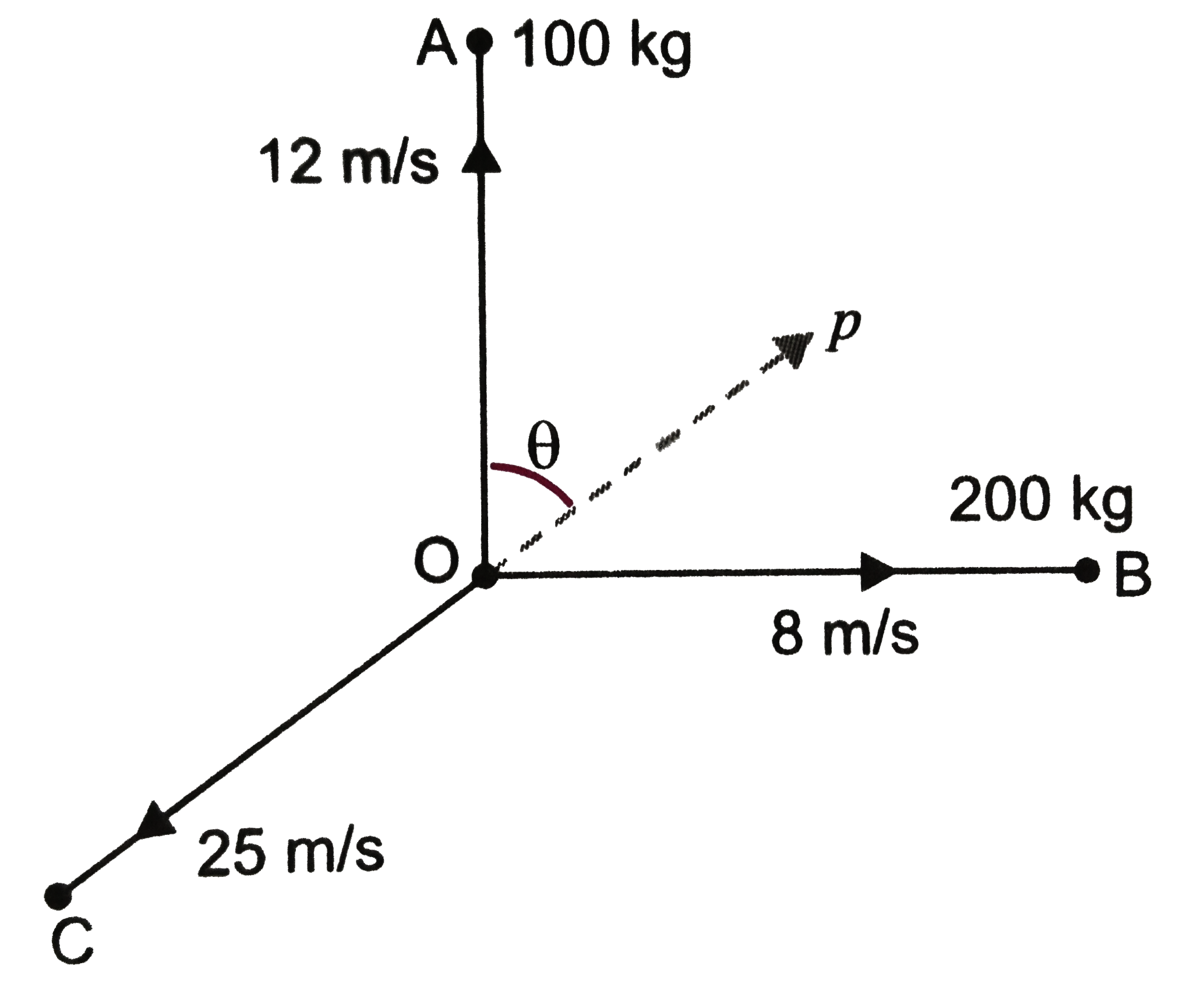
View SolutionA Diwali cracker of mass 60 g at rest, explodes into three pieces A, B and C of mass 10 g, 20 g and 30 g respectively. After explosion velocities of A and B are 30 m/s along east and 20 m/s along north respectively. The instantaneous velocity of C will be
View SolutionA 1 kg stationary bomb is exploded in three parts having mass 1 : 1 : 3 respectively. Parts having same mass move in perpendicular direction with velocity 30ms–1, then the velocity of bigger part will be : -
View SolutionA 5 kg stationary bomb is exploded in three parts having mass 1 : 3 : 3 respectively. Parts having same mass move in perpendicular directions with velocity 39m/s then the velocity of the bigger part will be :
View Solution
