The following Venn diagram shows three events, A, B, and C, and also the probabilities of the various intersections.
Determine
(a) P(A)
(b)
(c )
(d)
(e)
(f) Probability of the event that exactly one of A, B, and C occurs.

From the above Venn diagram,
(a)
(b)
= 0.07 + 0.10 + 0.15 - 0.15 = 0.17
(c )
(d)
(e)
(f) P (exactly one of the three occurs) = 0.13 + 0.10 + 0.28 = 0.51
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - PROBABILITY I EXERCISE - Exercise 9.16videos
PROBABILITY I
- BOOK - CENGAGECHAPTER - PROBABILITY I EXERCISE - Exercise 9.219videos
PROBABILITY I
- BOOK - CENGAGECHAPTER - PROBABILITY AND STATISTICSEXERCISE - Question Bank37videos
PROBABILITY AND STATISTICS
- BOOK - CENGAGECHAPTER - PROBABILITY IIEXERCISE - NUMARICAL VALUE TYPE2videos
PROBABILITY II
Similar Questions
The accompanying Venn diagram shows three events, A, B and C and also the probabilities of the various intersections [for instance,P(A∪B)=0.7]. Determine
(i) P (A)
(ii) P(B∩−C)
(iii) P(A∪B)
(iv) P(A∩−B)
(v) P(B∩C)
(vi) Probability of exactly one of the three occurs.View SolutionIf A and B are two independent events, prove that P(A∪B).P(A'∩B')≤P(C), where C is an event defined that exactly one of A and B occurs.
View Solution
Knowledge Check
- Question 1 - Select One
For two given events A and B P(A∩B)=
ANot less than P(A) + P(B) -1BNot greater than P(A) + P(B)CEqual to P(A)+P(B)−P(A∪B)DAll of the above - Question 2 - Select One
Fig. 24.8 shows three events A, B and C. Probabilities of different events are shown in the figure. For instance,
P(A∩B'∩C')=0.18 , P(A'∩B∩C')= 0.06 etc.
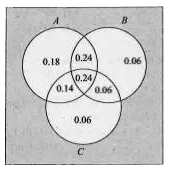
Which of the following is not true ?AA and B are independentBB and C are independentCA and C are independentDA and B∩ C are independent - Question 3 - Select One
If A and B are two events such that P(A∪B)+P(A∩B)=78 and P(A)=2P(B), then P(A) =
A712B724C512D1724
Three events A , B and C have probabilities 25,13and12 respecively. Given tat P(A∩C)=15andP(B∩C)=14, find the values of P(C/B)andP(A′∩C′)
View SolutionIf probabilities A and B are two independent events then P(A∩¯¯¯B)+P(A)P(B)=P(A). State true of false.
View SolutionIf P(B)=34,P(A∩B∩¯¯¯C)=13 and P(¯¯¯A∩B¯¯¯C)=13 then P(B∩C)=
View SolutionFor any two events A and B, if P(A∪B)=P(A∩B, then
View SolutionIf A and B are two events such that P(A∪B)=56,P(A∩B)=13 and P(¯¯¯B)=13 then P(A) =
View Solution

