(p∧~q)∧(~p∨q) is
A
a contradiction
B
a tautology
C
either (1) or (2)
D
neither (1) nor (2)
Video Solution
Text Solution
The correct Answer is:A
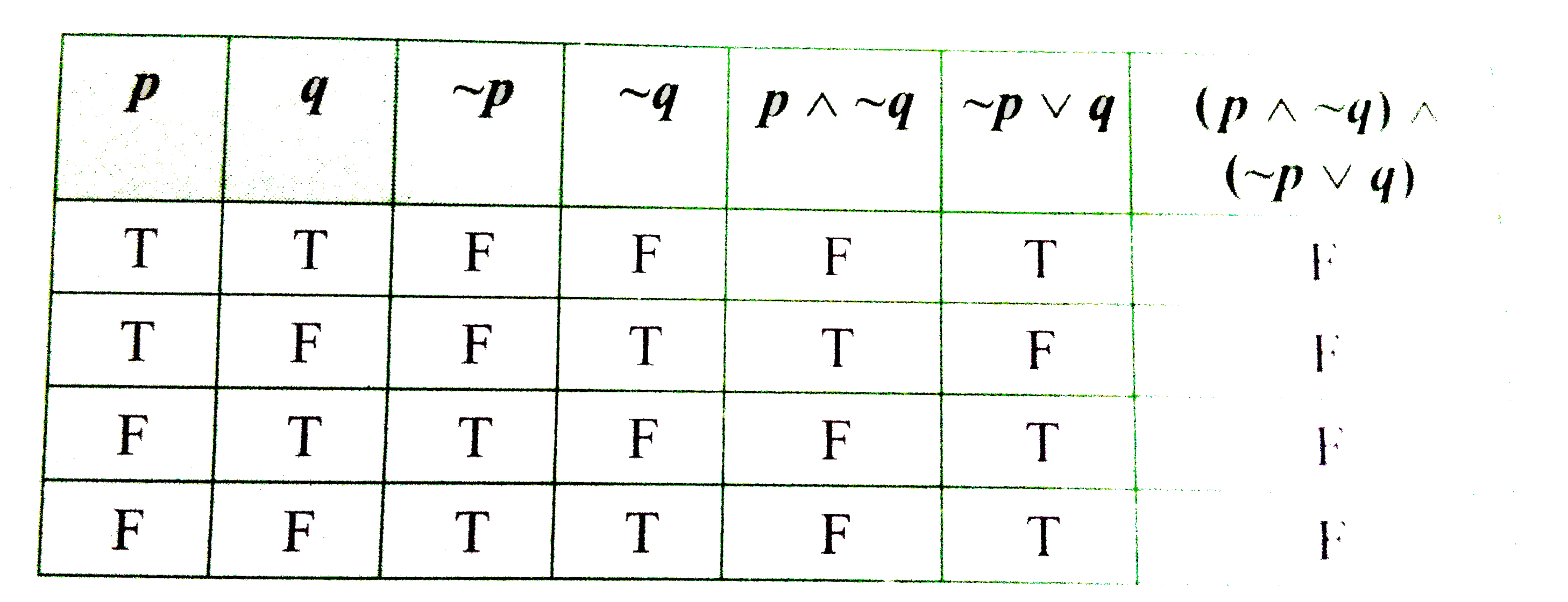
Clearly, (p∧~q)∧(~p∨q) is a contradiction
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - MATHMETICAL REASONINGEXERCISE - JEE Previous Year10videos
MATHMETICAL REASONING
- BOOK - CENGAGECHAPTER - MATHMETICAL REASONINGEXERCISE - Exercise 10.25videos
MATHMETICAL REASONING
- BOOK - CENGAGECHAPTER - LOGARITHM AND ITS PROPERTIESEXERCISE - JEE Previous Year5videos
LOGARITHM AND ITS PROPERTIES
- BOOK - CENGAGECHAPTER - MATRICESEXERCISE - Solved Examples And Exercises165videos
MATRICES
Similar Questions
Knowledge Check
- Question 1 - Select One
(p∧~q)∧(~p∧q) is a
AtautologyBcontradictionCtautology and contradictionDNeither tautology nor contradiction - Question 2 - Select One
(p∧~q)∧(~p∧q) is
Aa contradictionBa tautologyCeither (1) or (2)Dneither (1) nor (2) - Question 3 - Select One
Statement-1 : (p∧~q)∧(~p∧q) is a fallacy.
Statement -2: (p→q)↔(~q→~p) is a tautology .AStatement-1 is True, Statement -2 is Ture, Statement -2 is a correct explanation for statement -3BStatement-1 is True, Statement -2 is True,, Statement -2 is not a correct explanation for statement -3CStatement -1 is True , Statement -2 is false.DStatement -1 is False, statement -2 is True.
Construct the truth table for the followings statements :
(a) (p∧q)→~p (b)(p∧q)→(p∨q)
(c) (p∧q)→r (d)[p∧(~r)]→(q∨r)View SolutionIf p,q are two propositions then (p∨~q)∧(~p∧q) is
View SolutionThe Boolean Expression (p∧~q)∨q∨(~p∧q) is equivalent to : (1) ~p∧q (2) p∧q (3) p∨q (4) p∨~q
View SolutionUsing truth tables, determine wether the following statements are tautology or contradiction or contingency :
(1) ~(~p∧~q)∨q (2) [(p∨q)∧~p]∧(~q)View SolutionThe Boolean Expression ~(p∨q)∨(~p∨q) is equivalent to
View Solution

