Consider a pair of perpendicular straight lines .
The value of a is
A
1
B
3
C
2
D
-2
Video Solution
Text Solution
The correct Answer is:3
As the lines are perpendicular, Coefficient of Coefficient of
or
Also ,
Hence , the given pair of lines is
Factorizing , we get lines
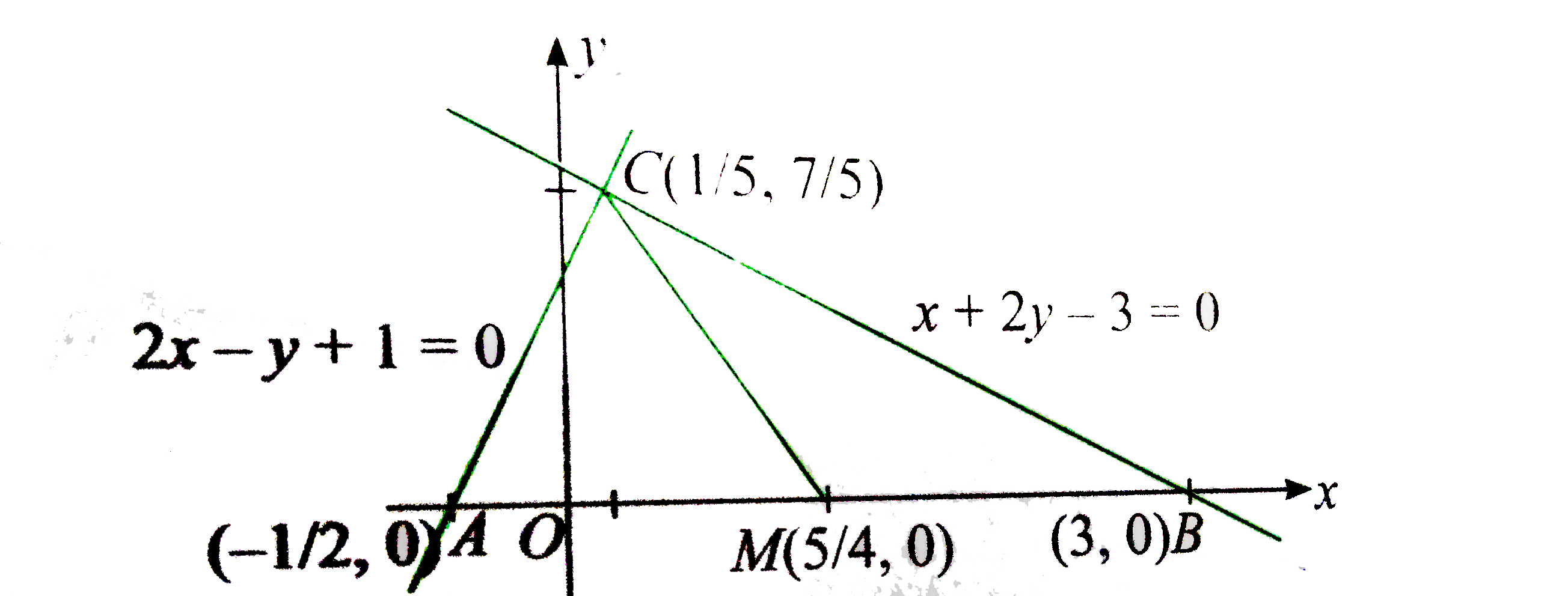
The point of intersection of the lines is C .
The points of intersection of the lines with the x- axis are A(3,0) and B .
The orthocenter of triangle is C and the circumcenter is the midpoint of AB which is M . Therefore,
CM
|
Topper's Solved these Questions
- PAIR OF STRAIGHT LINESBOOK - CENGAGECHAPTER - PAIR OF STRAIGHT LINESEXERCISE - Exercise (Numerical)
5 Videos
- PAIR OF STRAIGHT LINESBOOK - CENGAGECHAPTER - PAIR OF STRAIGHT LINESEXERCISE - Exercise (Multiple)
9 Videos
- MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONSBOOK - CENGAGECHAPTER - MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONSEXERCISE - Comprehension Type
6 Videos
- PARABOLABOOK - CENGAGECHAPTER - PARABOLAEXERCISE - Question Bank
21 Videos
Similar Questions
Knowledge Check
Consider a pair of perpendicular straight lines ax2+3xy−2y2−5x+5y+c=0.
The value of c isA-3B3C-1D1Consider a pair of perpendicular straight lines ax2+3xy−2y2−5x+5y+c=0.
Distance between the orthocenter and the circumcenter of triangle ABC isA4B9/2C8/3D7/4Consider a pair of perpendicular straight lines 2x2+3xy+by2−11x+13y+c=0 The value fo c is
A-2B2C-3D3
Consider a pair of perpendicular straight lines 2x2+3xy+by−11x+13y+c=0
The value of |b+2c|is
View SolutionConsider the equation of a pair of straight lines as x2−3xy+λy2+3x=5y+2=0
The value of λ is
View SolutionConsider the equation of a pair of straight lines as λx2−10xy+12y2+5x−16y−3=0. The angles between the lines is θ . Then the value of tanθ is
View SolutionConsider the equation of a pair of straight lines as λx2−10xy+12y2+5x−16y−3=0. The point of intersection of lines is (α,β). Then the value of αβ is
View SolutionConsider the equation of a pair of straight lines as x2−3xy+λy2+3x=5y+2=0
The point of intersection of line is (α,β) , then the value of α2+β2 is
View Solution
