Doubtnut Promotions Sticky

Consider the function f(x)={x−[x]−12x∉0x∈I where [.] denotes the fractional integral function and I is the set of integers. Then find g(x)max.[x2,f(x),|x|},−2≤x≤2.

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

We first draw the graphs of y=f(x),y=x2andy=|x|y=f(x),y=x2andy=|x|.
To deaw the graph of y=x−[x]−0.5={x}−0.5, we shift the graph of y={x},0.5 units downward vertically for non-nitegral values of x and plotting '0' for integral values fo x as shown in the following in the following figure.
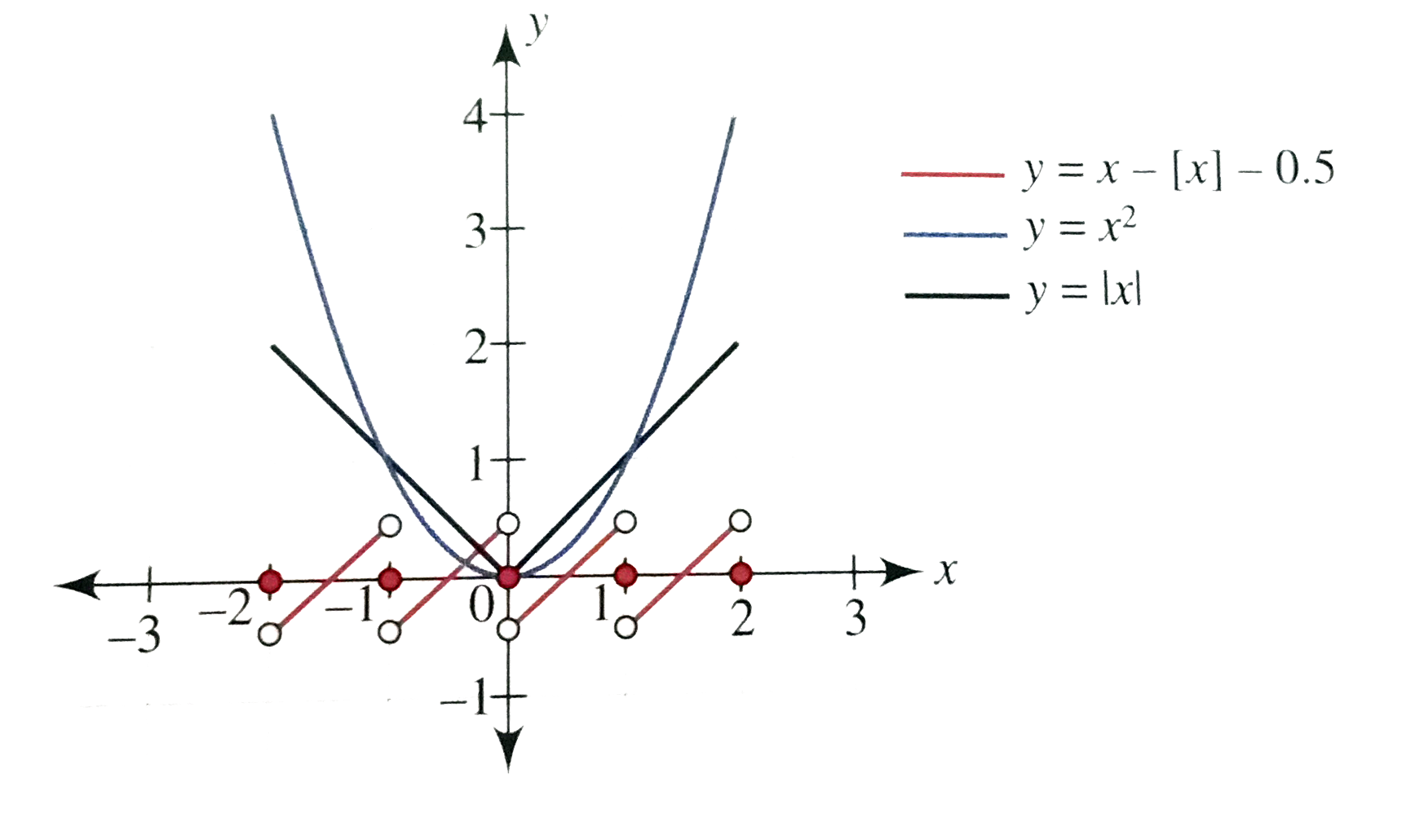
ocr_image
Clearly, from the graph, g(.x) =⎧⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎨⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎩x2,−2≤x≤−11−x,−1≤x≤−1/412+x,−14<x<01+x,0≤x≤1x2,1≤≤2

|
Updated on:21/07/2023
Class 12MATHSLINEAR PROGRAMMING

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Question 1 - Select One

    iff(x)={2x−[x]+sin(x−[x])x≠00x−0 where [.] denotes the greatest integer function then

    Af(X) is differentiable at x=0
    Bf(x) is differentiable at x=2
    Cf(x) is continuous but not differentiable at x=0
    Dnone of these
  • Question 2 - Select One

    The domain of function f(x)=log[x+12](2x2+x−1), where [.] denotes the greatest integer function is :

    A[32,∞)
    B(2,∞)
    C(−12,∞)−{12}
    D(12,1)∪(1,∞)
  • Question 3 - Select One

    The function f(x)=[x]+12,x∉I is a/an (wher [.] denotes greatest integer function)

    AEven
    Bodd
    Cneither even nor odd
    Deven as well as odd